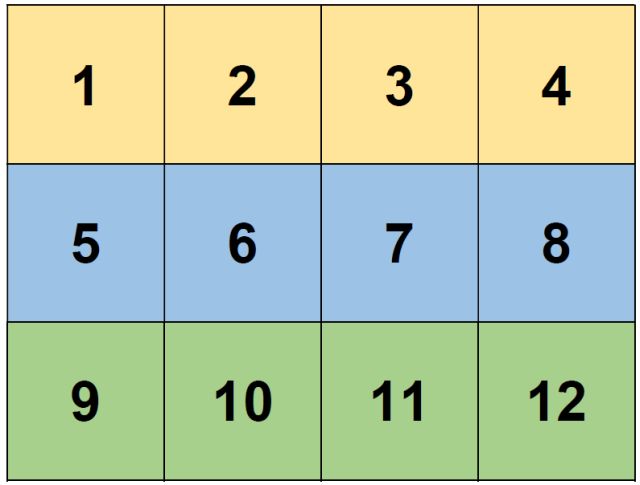
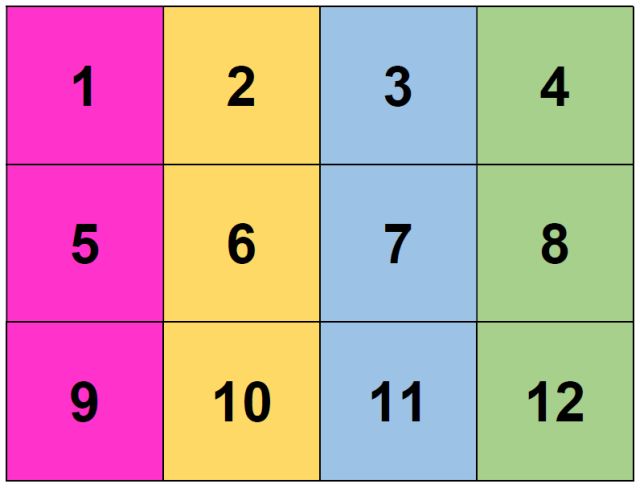
Alicia propone un juego a su amigo Benito y a su amiga Carmen. Elige una docena de cajas de cartón, las numera y las coloca en forma de cuadrícula 3×4, como muestra la imagen:
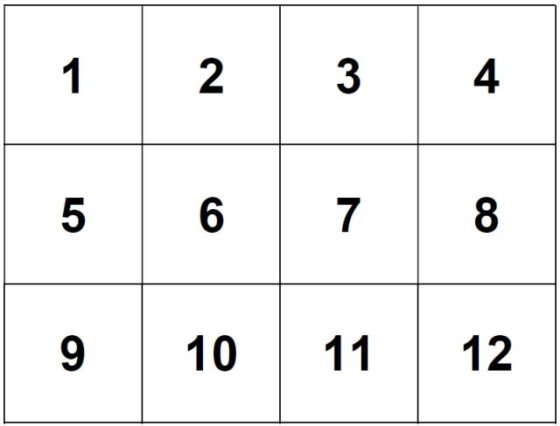
Alicia elige al azar dos de las cajas y esconde en cada una de ellas una chocolatina (son iguales), dejando el resto de las diez cajas vacías.
El juego consiste en lo siguiente:
Alicia muestra las cajas a Benito, quien debe ir abriéndolas por filas (es decir, en el orden 1-2-3-4-5-6-7-8-9-10-11-12) hasta que encuentre una de las chocolatinas. En ese momento se detiene. El número de cajas abiertas por Benito es su puntuación final.
Alicia vuelve a cerrar las cajas (dejando sus contenidos intactos) y se las ofrece a su amiga Carmen, quien las abrirá por columnas (es decir, en el orden 1-5-9-2-6-10-3-7-11-4-8-12), dejando de abrir cajas el momento de encontrar una chocolatina. Y, como en el caso de su amigo, anota el número de cajas que ha destapado hasta encontrar su primera chocolatina.
Gana este juego (y se come las dos chocolatinas) quien obtenga la puntuación más baja (quien haya encontrado antes el dulce). Y si empatan, Benito y Carmen se reparten el “botín”.
Por ejemplo, si Alicia esconde las chocolatinas en las cajas 8 y 11, Benito tendrá una puntuación de 8 (abre las cajas 1-2-3-4-5-6-7-8), mientras que Carmen obtendrá un puntaje de 9 (ya que destapará las cajas 1-5-9-2-6-10-3-7-11 hasta encontrar su primera chocolatina). Es decir, ganaría Benito.
La pregunta que se plantea es la siguiente: ¿Quién tiene más probabilidades de ganar el juego, Benito o Carmen? ¿O ninguno de los dos?
En primer lugar, recordemos que hay 66 maneras de repartir las dos chocolatinas introduciendo una en dos de las doce cajas (son las combinaciones sin repetición de 2 elementos elegidos entre 12).
Para estudiar el problema planteado, etiquetamos una caja con B o C dependiendo de quien de los dos (B-Benito y C-Carmen) llegue antes a esa caja, y escribiremos a su lado la puntuación obtenida (si allí hubiera chocolatina) por esa persona en cada caso. Además, la caja se marcará con X si, siguiendo cada uno su trayectoria, ambos llegan a esa posición en el mismo momento. Claramente, obtenemos el siguiente resultado:
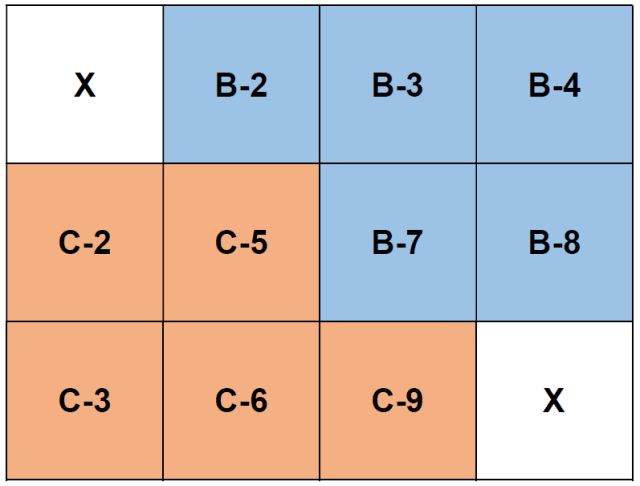
Observar que, si una chocolatina está en primera caja, Benito y Carmen empatan (hay 11 posibles posiciones para la segunda chocolatina), ya que ambos obtienen una puntuación de 1.
Si una chocolatina está en la última caja y la otra en una etiquetada con B o C, Benito gana en cinco ocasiones y Carmen en otras cinco.
Si las chocolatinas están escondidas en dos cajas etiquetadas con B, Benito gana (hay 10 reparticiones posibles). Del mismo modo, si las cajas con premio están ambas etiquetadas con C, es claro que gana Carmen (hay otras 10 distribuciones posibles).
El resto de los posibles repartos de las chocolatinas consiste en que una esté en una casilla etiquetada con B y la otra con C. Hay 25 maneras de que esto suceda. ¿Cuándo gana Benito? ¿Cuándo lo hace Carmen? ¿Cuándo empatan?
Benito gana (es decir, encuentra la primera chocolatina abriendo menos cajas que Carmen) si las chocolatinas están en:
-
B-2 y (C-3 o C-5 o C-6 o C-9),
-
B-3 y (C-5 o C-6 o C-9),
-
B-4 y (C-5 o C-6 o C-9),
-
B-7 y C-9,
-
B-8 y C-9.
Es decir, gana en 12 de las posibles posiciones de las chocolatinas en las cajas.
Y Carmen gana el juego (es decir, encuentra la primera chocolatina destapando menos cajas que Benito) si las chocolatinas están en:
-
C-2 y (B-3 o B-4 o B-7 o B-8),
-
C-3 y (B-4 o B-7 o B-8),
-
C-5 y (B-7 o B-8),
-
C-6 y (B-7 o B-8).
Es decir, gana en 11 de las 25 posibles posiciones de las chocolatinas en las cajas.
Benito y Carmen empatan si las chocolatinas están en alguna de estas 2 posiciones:
-
B-2 y C-2, o
-
B-3 y C-3.
Es decir, ¡Benito tiene más probabilidades de ganar que Carmen! ¿Por qué? Porque según el anterior análisis, Benito ganaría en 27 de los 66 casos posibles, Carmen lo haría en 26, y empatarían en 13… Aunque, recordemos, que eso no significa que no vaya a ganar Carmen.
Referencia
Egg Hunt, Futility Closet, 16 abril 2021
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad