Los lagos de Wada: un problema de topología
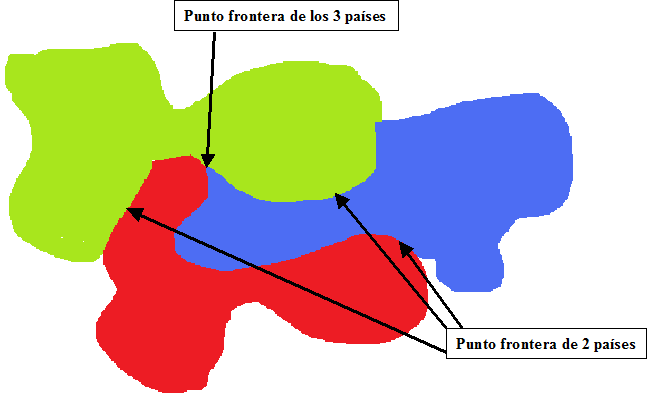
Imagina un mapa formado por tres países. Los países son abiertos –es decir, la frontera de un país no forma parte de él–y conexos –de una única pieza–. Dos de los países pueden compartir frontera, incluso los tres pueden hacerlo:
En un mapa ‘normal’ –¿cómo el dibujado arriba?– la intuición dice que los puntos frontera en los que concurren los tres países deben ser pocos…
Pero la intuición engaña a veces: de hecho, existen mapas en los que estos puntos son ‘muchos’. Un ejemplo muy conocido es el de los lagos de Wada, introducido en el artículo* y que lleva el nombre del topólogo Takeo Wada, profesor de Kunizô Yoneyama. Lo describimos a continuación.
Vamos a construir un mapa formado por tres conjuntos abiertos disjuntos y conexosi, y lo sorprendente de la configuración que vamos a describir es que la frontera de los tres países –en realidad van a ser lagos, de allí el nombre del ejemplo–… es la misma y consta de ‘muchos’ puntos.
Comenzamos con un cuadrado de lado 1 y abierto, formado sólo por zona seca.
Vamos a cavar tres lagos en este territorio siguiendo una regla muy precisa:
“Durante el día n = 1, 2, 3,…, debe extenderse el lago n (mód 3)ii de manera que pase a distancia menor que 1/n de todas las zonas secas que quedan. Esta construcción debe hacerse de manera la tierra seca resultante tenga interioriii conexo y cada lago sea un conjunto abierto.”
Para entenderlo mejor, vamos a describir lo que sucede en los primeros díasiv:
-
Se construye un lago azul de anchura 1/3 y longitud 2/3: la distancia de cualquier punto de zona seca al lago es menor que √2/3.
-
Se construye un lago rojo de anchura 1/32 como muestra la figura: la distancia de cualquier punto de zona seca al lago rojo es menor que √2/32.
-
Se construye un lago verde de anchura 1/33 como muestra la figura: la distancia de cualquier punto de zona seca al lago verde es menor que √2/33.
-
Se extiende el lago azul –recordar que los lagos deben ser conexos– mediante un canal de anchura 1/34: la distancia a cualquier punto de zona seca es menor que √2/34.
-
Se extiende el lago rojo mediante un canal de anchura 1/35: la distancia a cualquier punto de zona seca es menor que √2/35. La figurav muestra como se construyen estos canales.
El proceso continúa de este modo, y tras un número infinito de iteraciones –de días en los que los lagos se van ampliando con canales– quedan socavados tres lagos –azul, rojo y verde– que, por construcción, son conjuntos abiertos y conexos. Y también por construcción, puede demostrarse que la zona seca resultante –que es no vacía y tiene infinitos puntos– es la frontera de los tres lagos.
¡Un precioso y paradójico ejemplo topológico!
Notas:
* Kunizô Yoneyama, Theory of Continuous Set of Points, Tôhoku Mathematical Journal12, 143-158, 1917
i Son conceptos topológicos: de manera informal, un conjunto es abierto cuando no tiene ningún punto en común con su frontera y es conexo cuando es de una sola pieza.
ii n ≡ 0 (mód 3) si n es múltiplo de 3, n ≡ 1 (mód 3) si el resto de la división de n por 3 es 1 y n ≡ 2 (mód 3) si el resto de la división de n por 3 es 2. Por lo tanto, hablamos de tres lagos.
iii El interior de un conjunto es el conjunto sin sus puntos frontera.
iv No hay una única manera de hacerlo. La regla sólo precisa los detalles básicos.
v La figura muestra las cinco primeras etapas de la construcción de los lagos de Wada
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.





Luis GSA
Con pasos sucesivos de lo finito a lo infinito numerable se pueden hacer muchas cosas “contrarias a la intuición”. Una de ellas es transformar un arco del gráfico continuo de una función en un “serrucho” en el cual los dientes coincidan en el límite (todos con base cero en el arco). Con esto se obtiene un arco continuo para el cual no existe tangente (es decir derivada) en ninguno de sus puntos. Igualmente se puede lograr un arco de longitud infinita dentro de un área pequeña (en el serrucho anterior hay una) y una línea continua que pase por todos los puntos de un cuadrado. Paradójicamente estas construcciones “no intuitivas” son lo suficientemente intuitivas también.
Matemáticas | Annotary
[…] zientziakultura.com […]