Formulada por primera vez por el matemático francés Joseph Louis François Bertrand en su Calcul des probabilités (1888), la ‘paradoja de Bertrand’ es una paradoja de la teoría de la probabilidad que se enuncia del siguiente modo:
Consideremos una circunferencia C y una cuerda –un segmento cuyos extremos están situados sobre C– AB trazada al azar sobre ella.¿Cuál es la probabilidad p de que esta cuerda sea máslarga que el lado del triángulo equilátero inscrito en la circunferencia?
Abordando el problema de diferentes maneras, Bertrand obtuvo tres resultados distintos. ¿Cómo es posible? La pregunta clave es: ¿Qué significa trazar una cuerda al azar?
Veamos esas tres respuestas.
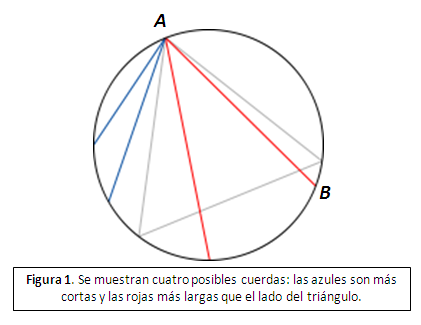
Respuesta 1: Elegimos Ay Bal azar sobre C.
Elegimos Aal azar sobre C y lo hacemos coincidir con uno de los vértices del triángulo inscrito. Para que la cuerda AB sea más larga que el lado del triángulo, Bdeberá elegirse sobre el arco de circunferencia determinado por el lado del triángulo opuesto al vértice A (ver la figura 1). Como el triángulo determina tres arcos isométricos, la respuesta es: p=1/3.
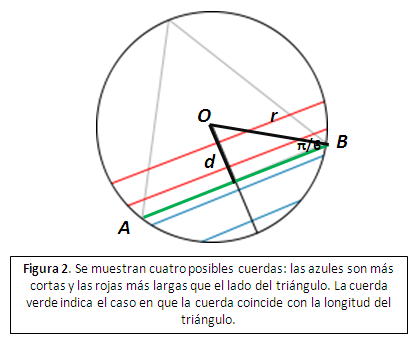
Respuesta 2: Elegimos ABteniendo en cuenta su distancia d al centro O de C.
Si el radio de C es r, en el caso extremo marcado en color verde en la figura 2, tenemos:
d= r sen (π/6)= r/2,
y por lo tanto, para que la cuerda AB sea más larga que el lado del triángulo, la distancia d al centro O de C no deberá exceder r / 2. Pero, la distancia maximal de una cuerda al centro de la circunferencia es r, por lo que la respuesta es p=1/2.
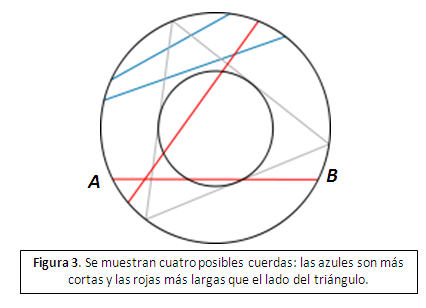
Respuesta 3: Elegimos AB teniendo en cuenta la posición de su punto medio.
Para que la cuerda AB sea más larga que el lado del triángulo, su punto medio debe de estar dentro del círculo inscrito en el triángulo, que es de radio r/2. Por lo tanto, la probabilidad p buscada es la razón entre el área del círculo inscrito (π r2/4) y el área del círculo determinado por C (πr2). Es decir, p=1/4.
Hemos llegado a tres respuestas diferentes al argumentar de distintas maneras, y las tres son correctas: hemos jugado con el azar eligiendo de manera aleatoria los puntos finales, la distancia al centro o el punto medio de la cuerda.
¿Cuál es el problema? Es la vaguedad del enunciado: el método que produce la variable aleatoria no está bien determinado, y ello puede dar lugar a manipulaciones ‘inconscientes’.
Nota: Las imágenes se han realizado en base a las encontradas en Wikipedia.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
La paradoja de Bertrand | Carlos Ernesto Martínez Rodríguez
[…] Formulada por primera vez por el matemático francés Joseph Louis François Bertranden su Calcul des probabilités (1888), la ‘paradoja de Bertrand’ es una paradoja de la teoría de la probabilidad que se enuncia del siguiente modo: para seguir leyendo ir al siguiente enlace Cuaderno de Cultura Científica […]
Edmond Nicolas Laguerre (1834-1886) |
[…] al apoyo de Joseph Bertrand, obtuvo una cátedra de físico matemático en el Colegio de Francia (1883) y se conviertió en […]
Adelantando en la autovía: una paradoja de la probabilidad
[…] situación contradictoria se parece a la famosa paradoja de Bertrand (de la que ya hablamos en este Cuaderno). El problema radica en que los datos proporcionados no son […]