En la entrada de hoy, del Cuaderno de Cultura Científica, vamos a fijar nuestra atención en la obra “Formas ritmo-espacio” (1966) del artista valenciano José María Yturralde, que nos servirá de motivación para introducirnos en algunas sencillas cuestiones matemáticas.

Antes de centrarnos en esta obra, presentemos brevemente a su autor.
José María Yturralde, pintor y artista valenciano (de origen navarro) reconocido mundialmente, es uno de los máximos exponentes de la abstracción geométrica en España y uno de los artistas más destacados del último tercio del siglo XX (y ahora también del siglo XXI) de nuestro país. Una característica fundamental de su obra es la profunda relación de esta con las matemáticas, así como la búsqueda de ideas y herramientas dentro de la ciencia y la tecnología. De hecho, fue uno de los primeros artistas en España en utilizar los ordenadores para pensar, crear y desarrollar el arte. En 1968 empieza a utilizar el ordenador durante su estancia en el Centro de Cálculo de la Universidad de Madrid, que fue el primer laboratorio español en utilizar la informática en el arte, de donde surgiría la exposición “Formas computables” (1969). Y después realizaría una estancia en el Centro de Estudios Visuales Avanzados del MIT (Instituto Tecnológico de Massachussets). Así mismo, ha sido pionero en España en el uso del láser, los hologramas y el video.
En su obra nos encontramos muy diversos temas matemáticos: figuras geométricas (triángulos, cuadrados, cubos, prismas,… polígonos y poliedros en general, o curvas como la astroide), proporciones, simetrías, orientación, perspectiva (cónica y esférica), ilusiones ópticas, banda de Moebius, la geometría de la cuarta dimensión y de dimensiones superiores, fractales, los conceptos de límite o vacío, etc… (véase su página web www.yturralde.org).




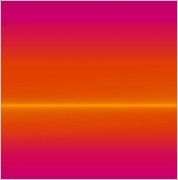
Pero vayamos a la obra de José María Yturralde con la que quiero que juguemos un poco en esta entrada, “Formas ritmo-espacio” (una de sus primeras obras). Este cuadro llamó mi atención cuando lo vi por primera vez, quizás por su estructura geométrica (sobre el lienzo cuadrado, los cuatro rectángulos forman una configuración con una simetría rotacional de 90º alrededor de un pequeño cuadrado central), el equilibrio de los elementos que lo componen o los colores elegidos. Pero no voy a hablar de su valor artístico aquí, sino de un par de cuestiones matemáticas sencillas que se pasaron por mi cabeza mientras lo observaba.
En primer lugar, la estructura geométrica de esta obra me recordó a la demostración visual (de la matemática norteamericana Doris Schattschneider) de la desigualdad entre la media geométrica y la media aritmética de dos números. Es decir, dados dos números positivos a y b, la media geométrica es menor o igual que la media aritmética
.
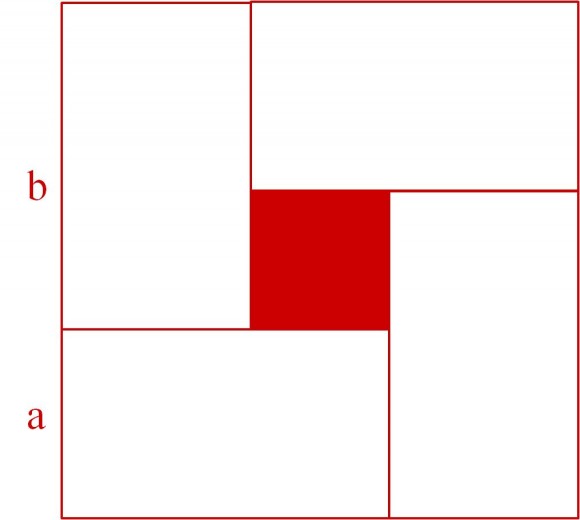
La demostración “sin palabras” de Schattschneider de este resultado matemático es la siguiente. Dados los números positivos a y b, consideramos el rectángulo de dimensiones a y b, realizamos cuatro copias y colocamos estas como en la imagen (cuya estructura es la misma que la del cuadro de Yturralde).
Claramente, el área del cuadrado grande menos el área del cuadrado pequeño es igual al de los cuatro rectángulos…
Por lo tanto,
Esta demostración apareció en la revista Mathematics Magazine en 1986, por lo que evidentemente no está relacionada con la obra de Yturralde.
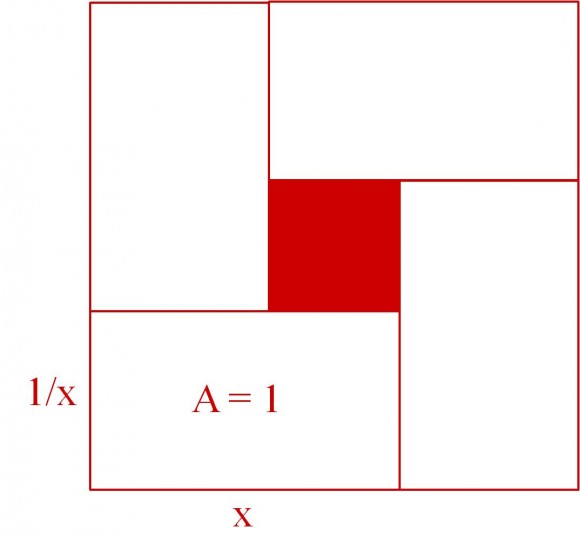
Mientras revisaba de nuevo el libro Demostraciones sin palabras, de Roger B. Nelsen, donde había visto la demostración visual de la profesora Schattschneider, descubrí otras dos demostraciones en las que se utilizaba el mismo esquema. La primera era una demostración de la propiedad matemática que dice que “la suma de un número positivo y su recíproco es mayor o igual que 2”. En esta ocasión, dado un número positivo x, cada uno de los cuatro rectángulos iguales que consideramos tiene unas dimensiones de x y 1/x, es decir, su área es igual a 1 (véase el dibujo).
Entonces, el área del cuadrado total, que es , es mayor –o igual, si x fuese 1–, a la suma del área de los cuatro rectángulos, que es 4. Es decir,
, y por lo tanto,
.
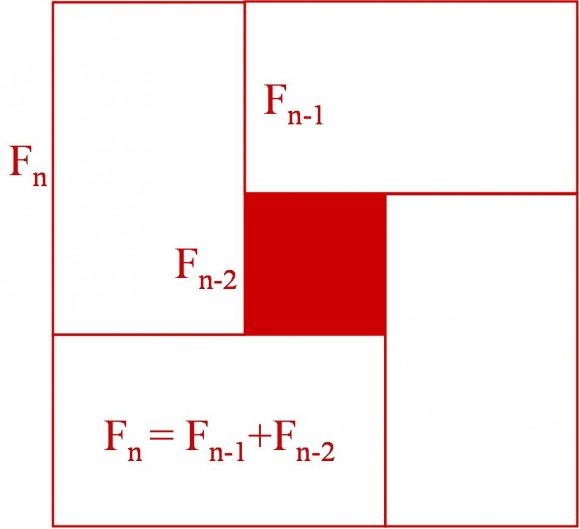
La segunda demostración es una igualdad entre los números de la sucesión de Fibonacci (famosa sucesión introducida por Leonardo de Pisa, Fibonacci, en su libro Liber Abaci de 1202, como solución al conocido problema de las parejas de conejos, y que está muy presente en la naturaleza –filotaxis- y en el arte). Recordemos que cada número de la sucesión de Fibonacci se obtiene como suma de los dos anteriores, es decir,
. Metiendo estas relaciones en el diagrama
se obtiene que .
La otra cuestión matemática (además de la simetría) que llamó mi atención observando “Formas ritmo-espacio” tenía que ver con las proporciones de los rectángulos. José María Yturralde ha utilizado diferentes proporciones (como por ejemplo, la razón áurea) en sus obras, en ocasiones de forma explícita y en otras participando en la estructura oculta que subyace a la parte visual de la pintura. El cuadro que nos interesa aquí, está formado por cuatro rectángulos iguales, por lo que nos podemos plantear qué proporción tiene cada uno de ellos… ¿la proporción áurea, la raíz de 2, alguna otra proporción dinámica, alguna de la proporciones estática usuales, como 3/2, 4/3 o 16/9, o ninguna proporción en especial?
Para contestar a esta pregunta tendríamos que medir las proporciones reales de los rectángulos y ver qué resultado se obtiene. Sin embargo, yo me he decantado en esta ocasión por una técnica más geométrica. Ya he manifestado al principio de esta entrada mi interés en jugar, no me interesa en este momento tanto el resultado en sí mismo como el camino a recorrer para obtenerlo. Para ello, simplemente he utilizado un compás sobre una imagen impresa de la obra (por lo que el lector o lectora de esta entrada puede poner todas las comillas que considere oportuno al comentario siguiente, sobre todo si tenemos en cuenta que no tenemos acceso al cuadro original, sino a una imagen de internet), y he tenido en cuenta las construcciones geométricas, a partir de un cuadrado, de los rectángulos áureo y raíz de un número natural, √n. El resultado obtenido es que, con las comillas que creáis oportuno, la proporción utilizada por Yturralde parece ser la proporción raíz de tres.
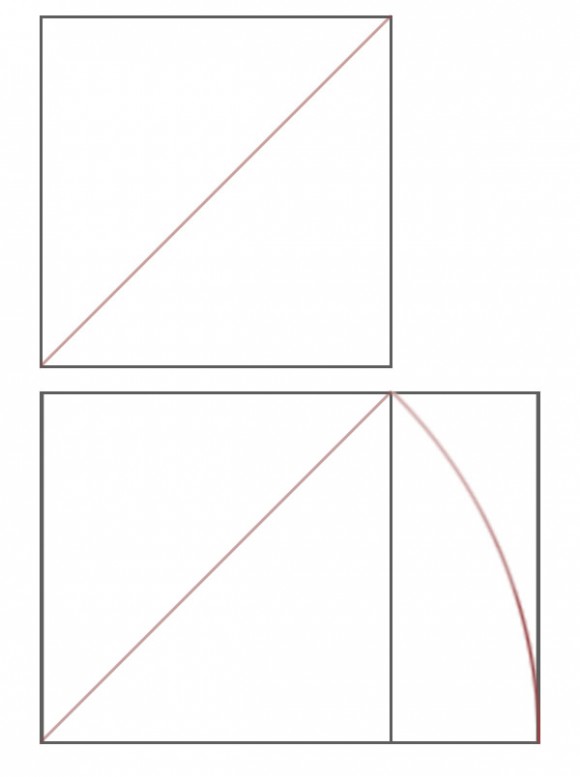
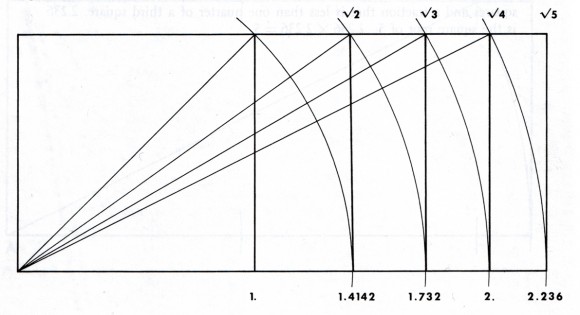
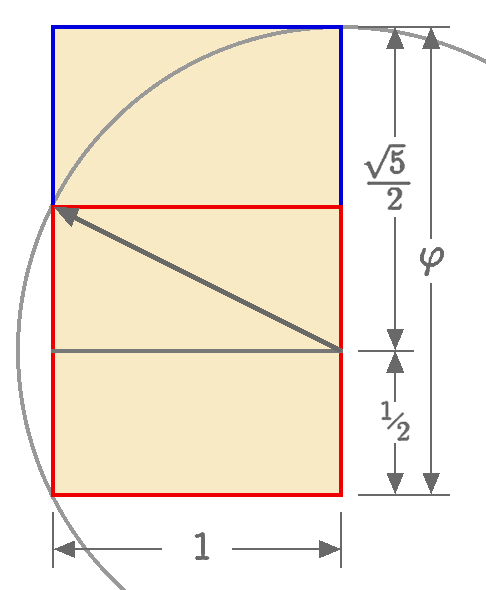
Expliquemos brevemente este tipo de construcciones, empezando por las proporciones √n. Dado un cuadrado inicial, que podemos considerar de lado 1, el teorema de Pitágoras nos dice que su diagonal es √2. En consecuencia, si trazamos un arco de circunferencia, centrado en uno de los vértices del cuadrado, nos estará marcando los puntos de distancia √2, y extendiendo uno de los lados del cuadrado hasta tocar la circunferencia habremos construido el lado de un rectángulo de dimensiones 1 y √2, luego de proporción √2.
Si ahora partimos del rectángulo √2, su diagonal (de nuevo por el teorema de Pitágoras) es √3, y trazando un arco de circunferencia como antes generaremos el rectángulo √3. De la misma forma se sigue para el resto de rectángulos de la forma √n.
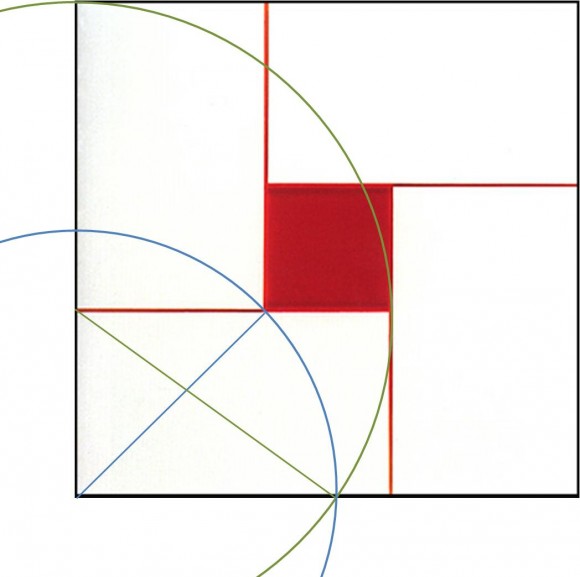
Ahora, ya estamos en condiciones de comprobar sobre el cuadro de Yturralde si la proporción utilizada podría ser, más o menos, raíz de n, para algún n. Y eso es precisamente lo que yo he hecho, aunque os muestro aquí una versión digital, obteniendo como resultado que el arco de circunferencia correspondiente con √3 es el que encaja con el rectángulo considerado.
Aunque ya no la necesitamos, os dejo a continuación la conocida construcción del rectángulo áureo (recordemos que la proporción áurea es ) a partir del cuadrado (que podemos considerar de lado 1)…
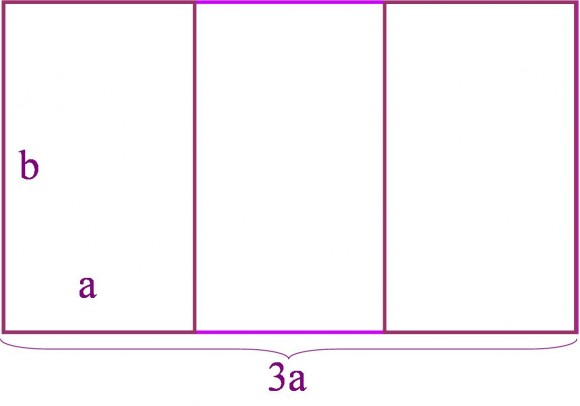
Para terminar esta entrada del Cuaderno de Cultura Científica, vamos a volver al arte para mostrar otra obra en la que está presente la proporción raíz de tres. El cuadro en cuestión es “Gólgota” (1964), del pintor abstracto Lucio Muñoz Martínez (Madrid, 1929 – 1998), que podéis visitar en el Museo de Bellas Artes de Bilbao.
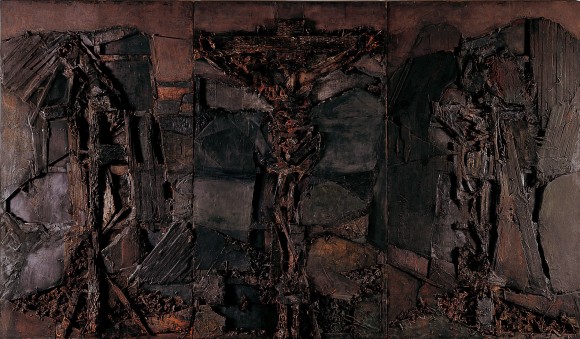
Como se observa, está formada por tres zonas rectangulares iguales (en la del centro está Jesús crucificado, y en las de los lados están los ladrones que fueron crucificados junto a Jesús), de forma que al poner juntas las tres zonas rectangulares, la proporción de la obra en su conjunto es igual a la proporción de cada una de las tres partes, lo que implica claramente, por geometría elemental, que la proporción del cuadro es raíz de 3.
Como la proporción del rectángulo grande es igual a la de los pequeños, , de donde se deduce que
.
Nota: Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas, cuyo anfitrión es el blog Cifras y Teclas.
Bibliografía:
1- Página web de José María Yturralde, www.yturralde.org
2- Doris Schattschneider, The aritmetic mean – geometric mean inequality, Mathematics Magazine 59, 1986.
3- Roger B. Nelsen, Demostraciones sin palabras, Proyecto Sur, 2001.
4- Roger B. Nelsen, Proofs without words II, MAA, 2000.
5- Roger B. Nelsen, The sum of a positive number and its reciprocal is at least two (four proofs), Mathematics Magazine 67, 1994.
6- Lucio Muñoz Martínez, Gólgota (1964), Museo de Bellas Artes de Bilbao (http://www.museobilbao.com/catalogo-online/golgota-8256)
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Resumen de la edición 4.123105 del Carnaval de Matemáticas | Cifras y Teclas
[…] Formas ritmo-espacio (Cuaderno de cultura científica) […]