Esos aburridos juegos simétricos

Les propongo un juego para dos personas, probablemente el juego de dados más simplón que se pueda imaginar. Las reglas son muy sencillas: cada jugador tira un dado, y el jugador con la puntuación más altagana.

Si jugamos con dados ordinarios, numerados del uno al seis, el juego no tiene demasiado interés. La probabilidad de victoriaes la misma para cada uno de los jugadores.

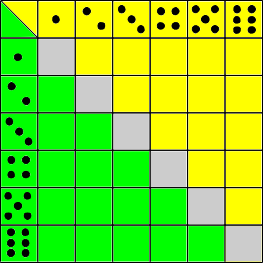
Para visualizarlo, imaginemos que el dado de un jugador es de color amarillo y el del oponente verde. Esto nos permite representar de un modo muy visual los 36 posibles desenlaces de una mano, representando en amarillo las victorias del dado amarillo, en verde las victorias del dado verde, y en gris los empates:

Observamos que de los 36 posibles desenlaces 15 son victorias amarillas y 15 victorias verdes. Es decir, la probabilidad de que gane cada uno de los jugadores es la misma (15/36), y por tanto ninguno tiene ventaja. Exactamente igual que si jugasen a lanzar una moneda al aire.

Otro modo de calcular las probabilidades sería notando que las reglas del juego son completamente simétricas para ambos jugadores. Ambos juegan con dados iguales, los turnos de lanzamiento son simultáneos, etcétera. Cualquier juego de azar que tenga exactamente las mismas reglas para todos los jugadores debe otorgar forzosamente a cada jugador la misma probabilidad de ganar.

Razonar de ésta manera puede resultar muy útil, no solo en el casino, sino también a la hora de detectar engaños. Sin embargo, como veremos más adelante, es fácil tomar por simétrico un juego que no lo es.

Un juego un poco más interesante

Añadamos algo de interés al aburrido juego de dados propuesto utilizando unos dados diferentes. Todos tienen 6 caras, pero la distribución de puntos es un tanto peculiar. Por ejemplo, el dado rojo tiene 1 “uno” y 5 “cuatros”.

Y el dado azul es así:

Y ya que estamos, fabriquemos un dado más en color naranja con éstos puntos:

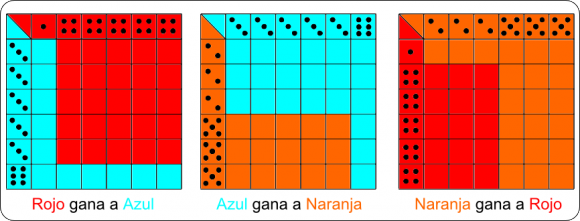
Ahora que tenemos tres dados,antes de empezar usted tiene que escoger con qué dado desea jugar, y supongamos que competirá conmigo. ¿Cuál será el mejor dado?, el mejor modo de averiguarlo es estudiando, una vez más, las tablas con los posibles resultados. Aquí están:

Es aquí donde empiezan las cosas raras. Si miramos los dos primeros diagramas, en los que rojo gana azul, y azul gana a naranja, podríamos pensar que el dado rojo es el mejor y el naranja el peor… hasta que miramos el tercer diagrama y descubrimos que, sorprendentemente, el dado naranja gana al rojo. Es decir, el que parecía el peor dado, gana al que parecía el mejor.

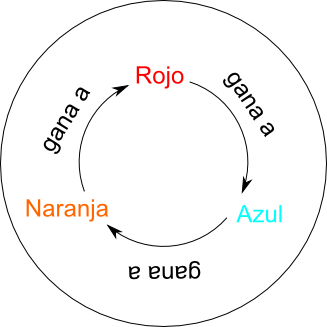
Es más claro verlo de ésta manera:

Los conjuntos de tres o más dados que cumplen ésta curiosa propiedad se conocen como dados no transitivos, y llevan estudiándose desde los trabajos pioneros de Bradley Efron.

La conclusión es muy llamativa: el dado escogido no importa, pero sí importa el orden en el que se escoge. El jugador que escoge dado en segundo lugar juega siempre con ventaja, pues ya sabe qué dado ha escogido el primer jugador y puede escoger el dado ganador. Sería un caso muy similar al de jugar a piedra, papel o tijera… pero sabiendo de antemano qué mano sacará el competidor. En un primer vistazo el juego puede parecer simétrico, pero no lo es en absoluto.

Se cuenta la anécdota de que el magnate norteamericano Warren Buffett, muy aficionado al análisis matemático de los juegos de azar, ofreció jugar a Bill Gates precisamente con el conjunto de dados que hemos descrito aquí… ofreciéndole, por supuesto, escoger primero. Parece ser que Gates pidió examinar los dados, y tras unos momentos de reflexión, cedió su turno a Buffett.

Otra patada a la intuición

La teoría de la probabilidad es, a pesar de su aparente sencillez, una de las ramas de las matemáticas más fecundas en paradojas de la intuición. Acabamos de ver una de ellas, pero no nos llevará demasiado esfuerzo toparnos con otra más: basta con añadir un tercer jugador.

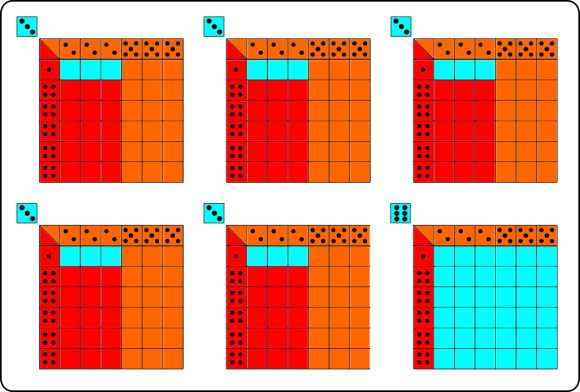
¿Cuál sería el mejor dado en éste caso? Si volvemos al diagrama que compara las parejas de dados, notaremos que la victoria más aplastante de todas ha sido la del dado rojo sobre el azul, con una probabilidad de victoria de 25/36.Podría pensarse que el dado rojo es, pues, la mejor opción en un juego con tres jugadores… y una vez más nos equivocaríamos. Como veremos enseguida, el mejor dado es el naranja.

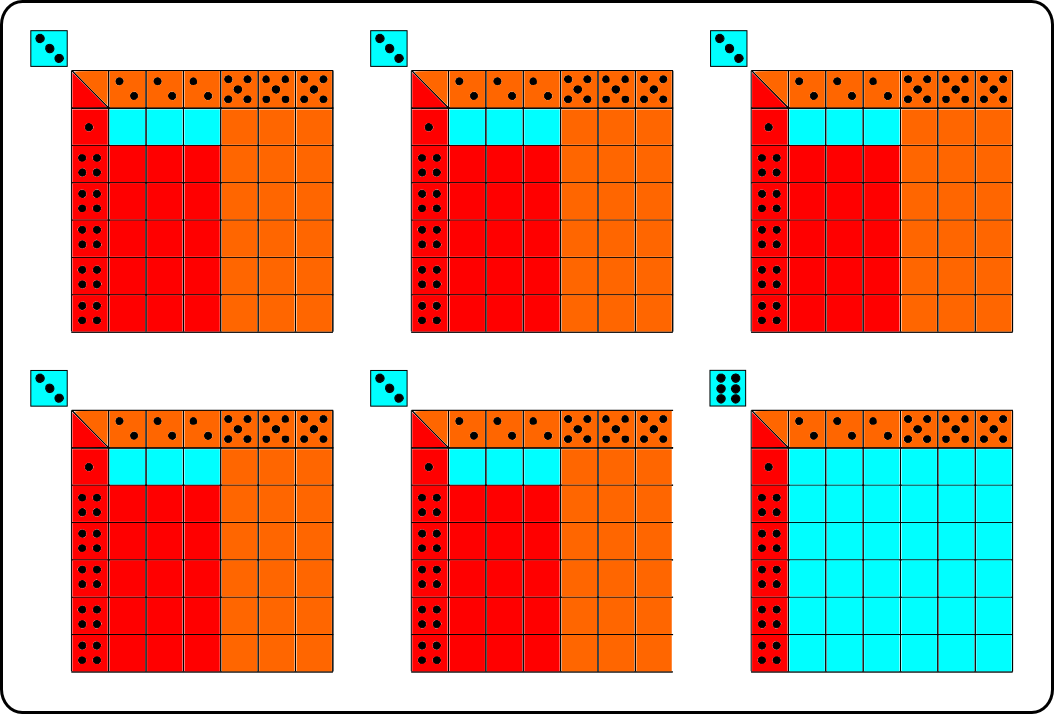
En el siguiente diagrama se representan las 216 posibles salidas de un juego con tres dados:

Siendo así las cosas, el dado naranja sería la mejor opción, con 90 victorias, seguido del rojo, con 75. El peor dado sería el azul, con solamente 51 opciones de ganar.

Como moraleja y consejo, desconfíen siempre de su intuición, pero muy especialmente cuando estén llevando a cabo razonamientos probabilísticos.

Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Fuentes y referencias:
– Non transitive dice, Wikipedia.
– Artículo sobre dados no transitivos en Gaussianos.