El mancala es una familia de juegos de los llamados “de siembra y recolección”, que se ha jugado y se juega a lo largo de todo el mundo, aunque es especialmente popular en África y algunas partes de Asia. Existen cientos de versiones, cada una con sus propias reglas y su propio tablero (tableros con 2, 3 y 4 filas de hoyos), así como multitud de nombres asociados a estos juegos (Anywoli, Awari, Awale, Ayo, Bao, Dakon, Nchuba, Oware, Wari,…). Aunque es interesante constatar que existen juegos de la familia mancala, en partes muy alejadas del mundo, con las mismas reglas, como es el caso del Awale cuyas reglas (aunque cambie el nombre) son las mismas en Ghana, Mozambique y Nigeria, en Barbados y Antigua, en Cabo Verde o en America del Sur, por citar algunos sitios.
El origen del mancala es desconocido, tanto el “cuándo” (a pesar de que existen indicios arqueológicos de agujeros distribuidos como en un tablero de mancala en el Neolítico y en la Edad de Hierro, así como en pirámides y templos de la zona de Egipto, no está claro que correspondan a tableros de Mancala o incluso existen dudas razonables sobre las fechas de su realización), como el “dónde” (expertos como A. J. de Voogt han puesto de manifiesto la inconsistencia de la extendida creencia en el origen egipcio, y apuestan por el estudio de la similitud de las reglas en diferentes partes del mundo, y la migración humana que pudo llevar a ello).
Dentro de la familia mancala existe un juego solitario de una sola fila de hoyos, que es el Tchuka Ruma. De nuevo, el origen de este juego es desconocido. En el artículo de P. J. Campbell y D.P. Chavey, titulado Tchuka ruma solitaire (UMAP Journal 16, 1995), se incluye un apéndice sobre la cuestión del origen de este solitario. Según algunos expertos podría ser la India, Filipinas, Maldivas o Rusia, aunque los autores se decantan por la zona de Malasia e Indonesia, teniendo en cuenta el origen etimológico del nombre del juego.
La primera publicación en la que se habló del juego parece ser que fue el artículo Jeu de la Tchouka, del matemático Henri-Auguste Delannoy (1833-1915), en el que menciona que ha tenido conocimiento del mismo a través de su correspondencia con el también matemático francés Edouard Lucas (1842-1891), autor del libro Recreaciones matemáticas, por lo que podría ser una invención de éste basada en un juego ya existente.
Pero como lo más importante en un juego es “jugar”, vayamos directamente con la descripción y reglas del juego. El tablero del Tchuka Ruma consta de 5 hoyos en fila, los cuatro primeros son del mismo tamaño y contienen, cada uno, dos “semillas” (alubias, piedras, botones o fichas) en la posición inicial (en total 8 semillas) y un quinto hoyo más grande, que es la “Ruma”, almacén donde se recogerán las semillas y que estará inicialmente vacío.
El juego consiste en que el jugador realice una serie de movimientos de las semillas destinados a que todas terminen almacenadas en la Ruma. Para lo cual, el jugador deberá seguir las siguientes reglas…
i) se cogen las “semillas” de un hoyo, o cuenco, cualquiera y se reparten, una a una, en los siguientes hoyos (movimiento que se denomina “siembra”), avanzando en dirección hacia la Ruma (el almacén), si este está en la derecha, se siembra de izquierda a derecha;

ii) si una vez colocada una ficha en el Ruma, aún quedan fichas en la mano, se continúan colocando fichas por la otra parte del tablero (en el caso de que el Ruma este en la derecha, sería por la izquierda);
iii) cuando se coloca la última ficha, en una siembra, pueden ocurrir tres cosas:
a) que el hoyo en cuestión tenga más fichas, entonces se cogen todas las fichas de ese cuenco y se distribuyen como se ha explicado anteriormente;
b) que caiga en la Ruma, entonces se deja la semilla allí y se elige un hoyo cualquiera (que no sea la Ruma) para continuar sembrando;
c) que se coloque en un cuenco que no tenía fichas, en ese caso el jugador ha perdido la partida, y habrá que comenzar de nuevo desde el principio (como ocurre en la imagen anterior);
iv) el juego termina cuando el jugador consigue almacenar todas las fichas en la Ruma.
Una vez que hemos entendido bien las reglas de este sencillo solitario, no solo estamos en condiciones de jugar, sino que es imprescindible jugar.
Construir un tablero es bastante sencillo. La opción más sencilla es pintar en un papel cinco círculos, o cuadrados, en fila, el último más grande que los otros, y utilizar fichas del parchís. Otra posibilidad es utilizar vasos, tazas, cuencos o como he hecho yo en mi casa, “moldes de colores para magdalenas”. O incluso se pueden hacer agujeros en el suelo, si estáis al aire libre. Las “semillas” pueden ser casi cualquier cosa, como piedras, botones, alubias o canicas.
Y aunque yo recomiendo jugar con una versión material, se puede jugar a la versión online (de aspecto circular)…
A continuación, vamos a ver cómo resolver el juego. Lo primero que habréis hecho es simplemente jugar, con lo cual además de pasarlo bien, habréis llegado a conocer bien el juego. Y como es un juego sencillo, es probable que ya lo hayáis resuelto en esa fase inicial. En cualquier caso, veamos cómo enfrentarnos a la resolución del Tchuka Ruma. Habría dos formas de enfocar el problema, un análisis exhaustivo de las diferentes posibilidades del juego o plantear un razonamiento “de atrás hacia delante”.
Empecemos con el análisis de todas las jugadas posibles. En la posición inicial, que denotamos22220, podemos empezar por cualquiera de los cuatro hoyos. Veamos qué ocurre en cada caso.
1er hoyo) 22220 – 03320 – 13031 (la semilla cae en 0, hoyo vacío, y el jugador pierde)
2º hoyo) 22220 – 20330 – 31301 – 02411 (en 0 y pierde)
3er hoyo) 22220 – 22031 – en la Ruma, luego hay 3 opciones…
i) 03131 (en 0, pierde)
ii) 20141 – 31202 – 31013 – en la Ruma, 3 opciones…
a) 02123 – 12104 (en 0, pierde)
b) 30113 (en 0, pierde)
c) 31004 – en la Ruma, pero solo hay dos opciones y son perdedoras, 02114 ó 30104
iii) 33002 – 30113 – en la Ruma y de nuevo 3 opciones…
a) 01223 – 11204 (en 0, pierde)
b) 30023 – 40004 – 01115 – en la Ruma y 3 opciones más…
b1) 00215 – 00026 – 10007 (pierde)
b2) 01025 – 11006 (pierde)
b3) 01106, en la Ruma, y hay dos opciones, una
ganadora, 00206 – 00017 – 00008 y otra
perdedora, 01016
c) 30104 , en la Ruma, pero las dos opciones son perdedoras, 01214 ó 30014
4º hoyo) 22220 – 32201 – 03311 (en 0, pierde)
Tras analizar todas las jugadas posibles, hemos llegado a la conclusión de que existe una única solución, que es…
22220 – 22031 – 33002 – 30113 – 30023 – 40004 – 01115 – 01106 – 00206 – 00017 – 00008
Otra forma de abordar la búsqueda de una solución al juego sería razonar “de atrás hacia delante”, es decir, partimos de la situación final (00008) y pensamos cual puede ser la posición anterior (solo puede ser 00017) y así continuamos como se muestra en la imagen…
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() En cada movimiento hacia atrás hay que ir discriminando las situaciones malas, que no nos llevarán a la posición inicial.
En cada movimiento hacia atrás hay que ir discriminando las situaciones malas, que no nos llevarán a la posición inicial.
En general, podemos plantearnos jugar al Tchuka Ruma de cualquier número de hoyos (digamos n, sin contar la Ruma) y con un cierto número (digamos k) de semillas en cada hoyo. En tal caso podemos estudiar qué ocurre en cada juego (n,k) y veremos que hay casos para los que no existe solución. Como por ejemplo, n = 4 –cuatro hoyos- y k = 3 –tres semillas por hoyo-, donde el número máximo de semillas que se puede llegar a almacenar en la Ruma es 7.
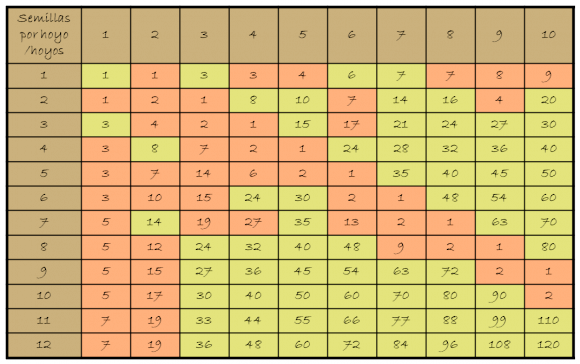
En 1995, los matemáticos estadounidenses P. J. Campbell y D.P. Chavey realizaron un estudio matemático del Tchuka Ruma (en su versión general de n hoyos y k semillas por hoyo), en el que analizaban la existencia de soluciones para este juego. Encontraron algunas familias de juegos Tchuka Ruma (n,k) que no tienen solución, y demostraron que dado un Tchuka Ruma (n,k) es imposible saber si tiene solución, salvo si se construye explícitamente una. Además, computaron el comportamiento de los juegos para n y k menores o iguales a 100.000, comprobando que (como empieza a verse en la imagen anterior) para valores grandes de n y k, los juegos que no tienen solución son los de las diagonales n = k y n = k+1 (en rojo en la imagen).
Algunas variantes del Tchuka Ruma son:
a) El Multichouka, que es como el Tchuka Ruma, pero de distribución libre de semillas en cada agujero;
b) el Tchoukaillon, en el cual el jugador decide cuántas semillas coloca en cada hoyo, la última semilla de cada siembra debe ir a la Ruma y “no es circular”;
c) el Monokalah, que es como el anterior, pero sí sería “circular”.
Bibliografía
1.- Alexander J. de Voogt, Distribution of mancala board games: a methodological inquiry, Journal of Board Games Studies 2,104-114, 1999.
2.- Página web AWALÉ (castellano, catalán, inglés)
3.- Grupo Alquerque de Sevilla, Tchuka Ruma, www.divulgamat.net (sección Recursos on line, apartado de Juegos Matemáticos)
5.- Jeroen Donkers, Jos Uiterwijk and Alex de Voogt, Mancala games – Topics in Mathemathicsand Artificial Intelligence, Journal of Machine Learning, 2001.
6.- P. J. Campbell, D.P. Chavey, Tchuka ruma solitaire, UMAP Journal 16(4), 343-365, 1995
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Esta entrada participa en la edición 4.12310562 del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews







Creades
He leído todo hasta donde pone «ahora vamos a ver como resolver el juego…» Esto me lo guardo para más adelante jejeje
Mientras leía el funcionamiento recordé que en un móvil de hace bastantes años tenia un juego similar que era bastante entretenido, no recuerdo el nombre, pero casi estoy segura que sería este del que hablas.
Ya volveré más adelante a leer la solcuión!
Saludos 🙂
Carnaval de Matemáticas: resumen de la edición 4.12310562 | :: ZTFNews.org
[…] 4: Tchuka Ruma, el mancala solitario desde el Cuaderno de Cultura […]
Carnaval de Matemáticas | Matemáticas Secundaria
[…] 4: Tchuka Ruma, el mancala solitario desde el Cuaderno de Cultura […]