Teorías fantásticas sobre el origen de la grafía de las cifras
Recientemente alguien me ha recordado en twitter un “famoso” powerpoint que circuló hace algunos años por la red, y que fue enviado masivamente a través del correo electrónico (a mí me llegó varias veces). El tema del mismo era el origen de la representación escrita de las cifras de nuestro sistema de numeración (los llamados números arábigos o indo-arábigos). Yo lo llamé por aquel entonces la teoría del powerpoint, y aún hoy en día puede encontrarse en muchas páginas web y blogs.
Según ese powerpoint, cada cifra se representa con una forma, trazada a base de rectas, cuyo número de ángulos coincide con el valor numérico de la misma. Así, la representación gráfica del 1 tiene un ángulo, la del 2 consta de dos ángulos, así hasta el 9, del que se muestra también una forma, cercana a la escritura actual, en la que pueden apreciarse nueve ángulos, y por supuesto, el cero, redondo, no tiene ángulos.
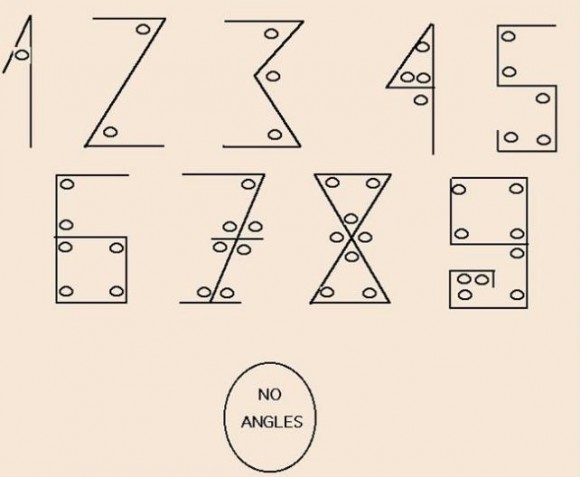
Seguro que vosotros también lo recibisteis en alguna ocasión. Muchas personas al verlo pensaron “¡qué interesante!” y se lo enviaron a su vez a amigos y conocidos. Pero este powerpoint no es más que un sencillo ejemplo de los posibles peligros de internet (aunque ahora solamente me estoy refiriendo al conocimiento y no de otros temas más delicados). Pero, en definitiva, ¿será cierto que este es el origen de la grafía de las cifras indo-arábigas?
Hablando con muchas personas, descubrí que daban por buena esa teoría de la explicación de la representación gráfica de las cifras por medio de los ángulos. Incluso hubo quien me sugirió que subiéramos el powerpoint a la página divulgamat (centro virtual de divulgación de las matemáticas, de la Real Sociedad Matemática Española, www.divulgamat.net).
Por lo que yo conocía sobre el origen de las cifras indo-arábigas, la teoría del powerpoint no tenía ninguna lógica, pero además si uno se fija un poco en las representaciones, la supuesta relación de la grafía con los ángulos parecía un argumento bastante artificioso, “gracioso” pero sin fundamento. Más aún, en casos concretos como el 7 o el 9, la verdad es que está muy pillada por los pelos.
Aunque, si existen dudas lo mejor es acudir a la historia de los números, y a los expertos en esta materia. Uno de esos expertos es Georges Ifrah, y una referencia obligada su texto “Historia Universal de las Cifras”.
Por lo que se sabe, la grafía de los números modernos –así como todo nuestro sistema de numeración, arábigo o indo-arábigo– tiene su origen en la India, de donde pasaría a los árabes, y de ellos a Europa, en un viaje que duraría más de 1.000 años. Además, a lo largo de todo ese tiempo la representación gráfica de las cifras iría evolucionando continuamente, hasta llegar a las definitivas y actuales cifras.
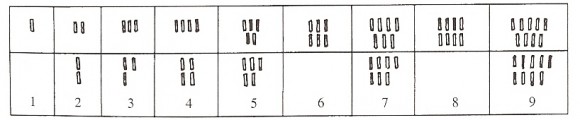
Las primeras representaciones escritas de los números en la antigüedad fueron, normalmente, mediante la repetición de “rayas” (desde las efímeras muescas sobre un palo o un hueso, a sistemas de escritura más elaborados y permanentes), que se utilizaban para representar el número como repetición de la unidad. Si nos fijamos por ejemplo en el número 2: i) dos palos verticales paralelos, eran utilizados por egipcios, etruscos, antiguos griegos, fenicios, arameos, cretenses o romanos, entre muchos otros pueblos; ii) en China o la India, por ejemplo, se utilizaron dos palos horizontales paralelos; iii) los babilonios utilizaron dos “clavos” horizontales; iv) aunque algunos pueblos, como los mayas, utilizaron otras grafías simples, como dos puntos.
Muy lejos de esas representaciones primitivas, se encuentran las cifras europeas modernas, cuyo origen está en las cifras brahmi, que aparecieron en la India entre los siglos III a.c. y II d.c. La evolución de las cifras brahmi hasta las cifras actuales, consolidadas en Europa en el siglo XV, se produjo en un largo periplo de muchos siglos a través de vastos territorios de nuestro planeta, desde su origen en la India, pasando por los territorios árabes (Oriente Medio primero y después el norte de África), hasta llegar a Europa, a través de la Península Ibérica. Fue una evolución continua, con grandes modificaciones temporales, así como territoriales. En aquellos tiempos había muchísimos sistemas de numeración locales, junto al brahmi y posteriores, que se interrelacionaban unos con otros y evolucionaban sin fin.
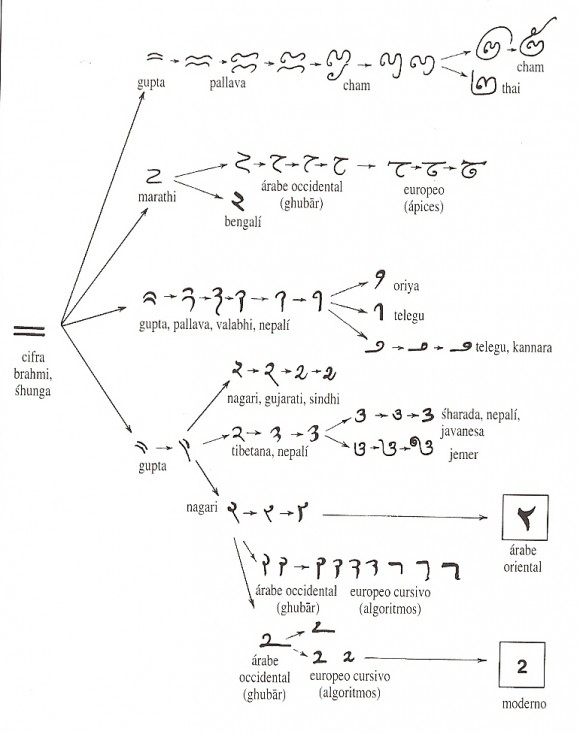
En el siguiente cuadro vemos cómo fue evolucionando la grafía del número dos, desde su representación mediante “dos líneas horizontales paralelas” en el sistema de numeración brahmi hasta llegar a las cifras modernas del dos, tanto la árabe (de la que no hemos hablado en esta entrada), como la europea. Y puede observarse además, como algunas grafías acabarían por desaparecer.
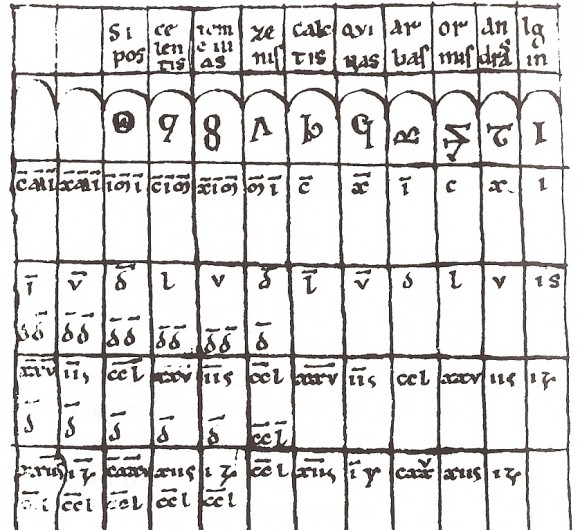
La primera aparición de las cifras indo-arábigas, del 1 al 9, en Europa fue en el Codex Vigilanus (976 d.c.), o Manuscrito de Vigilán, en el Monasterio de San Martín de Albelda, de La Rioja.

Sin embargo, estas no son las que darían lugar a las cifras modernas, sino que son una rama paralela de evolución de las cifras indo-arábigas, las cifras llamadas “ápices”, de la edad media, que luego desaparecerían. Mientras que las utilizadas hoy en día derivan de la segunda forma de las cifras europeas, llamadas “algoritmos”.
Este brevísimo resumen del origen y evolución de las cifras indo-arábigas nos pone de manifiesto lo absurdo de una interpretación racional y estática de dicho origen, como es la hipótesis del powerpoint, y la relación entre cifras y ángulos.
De hecho, si consultamos el libro “Historia universal de las cifras”, resulta que encontraremos información sobre el origen de esta “teoría del powerpoint”. Esta es una de las explicaciones fantásticas a propósito del origen de las cifras “árabes”, que comenta Georges Ifrah. El historiador de las matemáticas afirma que según una leyenda popular de Egipto y el norte de África, las cifras “arábigas” (nuestras cifras modernas) fueron inventadas por un vidriero geómetra originario del Magreb, con el objetivo de dar a cada una de las nueve cifras (1, 2, 3, 4, 5, 6, 7, 8, 9) una forma que evocara su valor numérico a través del número de ángulos contenidos en el trazado de las mismas.

Según Howard W. Eves, en su libro “Mathematical Circles” (volumen II), la directora de un museo de Marruecos, Mrs. Abdelkri Boujibar, publicó hace no mucho tiempo un artículo en el que recuperaba esta teoría, y la ponía así de moda, en cierto sentido.
Volviendo al libro de Ifrah, esta teoría también aparece en la obra de un autor francés P. Voizot, de finales del siglo XIX, quien pudo tomarla a su vez de un genovés. Además, este francés consideraba igualmente probable, una explicación por encaje de trazos. Es decir, el 1 es un trazo vertical, para el 2 se dibujan dos trazos horizontales y al unirlos aparece esta cifra (pensemos que en el movimiento de trazado rápido de dos líneas horizontales a menudo solemos arrastrar el lapicero y dejar marcada la curva que nos generaría la cifra 2), el 3 es la unión de tres trazos horizontales, el cuatro serían cuatro trazos, y así hasta el 9. Aunque la verdad a partir del número 5 no tiene mucho sentido. Es lo que Ifrah llama la segunda hipótesis fantástica.
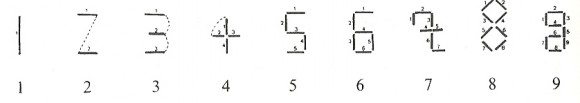
O incluso existió un español del siglo XVIII, Carlos el Moro, quien sugiere un origen muy cercano al de los ángulos de la “teoría del powerpoint” (la quinta hipótesis fantástica).

Pero existen más hipótesis fantásticas, aunque no se hayan hecho tan populares como la “teoría del powerpoint”. Por ejemplo, la tercera hipótesis fantástica que procede del siglo XVII y que toma como referencia el número de puntos que habrían servido inicialmente para realizar un representación pictográfica de las nueve cifras.

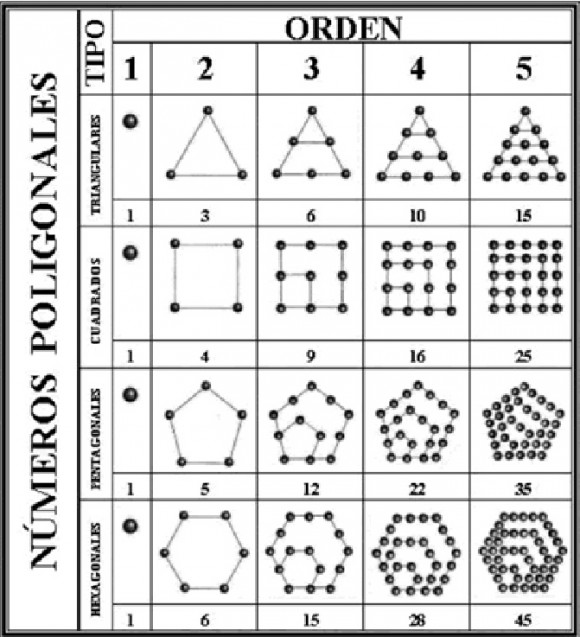
Lo curioso de esta teoría, es que en el siglo XIX un francés la tomó para intentar justificar el supuesto origen griego de nuestro sistema de numeración, en concreto, el origen pitagórico. La secta de los seguidores de Pitágoras trabajó con los números poligonales, números trazados mediante cálculos (piedras, o puntos en los dibujos) al disponerlas geométricamente según una cierta forma, y obtuvieron resultados numéricos mediante relaciones geométricas de estos.
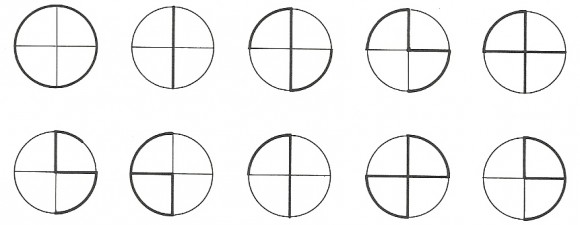
Y existen otras dos teorías bastante fantásticas. La cuarta hipótesis fantástica descrita por Ifrah, al parecer propuesta por el astrólogo árabe Aben Ragel (siglo X-XI), aseguraba que las cifras habían sido resultado de una división de la figura formada por una circunferencia y dos de sus diámetros en forma de cruz. Es decir, todas las cifras pueden ser descritas con partes de esa figura base. El diámetro vertical sería el 1, ese diámetro junto con dos arcos opuestos de la circunferencia situados en los extremos del diámetro serían el 2, el semicírculo derecho con el radio horizontal derecho sería el 3, y así sucesivamente.
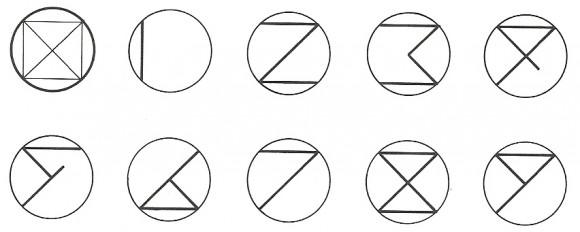
Y la sexta hipótesis, propuesta por el físico, ingeniero y matemático alemán Jacob Leupold en el siglo XVIII, es similar a la anterior, pero con un círculo, un cuadrado inscrito y sus diagonales.
La “teoría del powerpoint” en particular, pero también el resto de estas hipótesis fantásticas, nos muestran el origen de la representación gráfica de las cifras como una creación racional, y realizada por un solo individuo, y no como lo que fue en realidad… fruto de la evolución temporal y espacial, a través de muy distintos pueblos.
Referencias:
Georges Ifrah, Historia universal de las cifras, Espasa Calpe, 2002.
Antonio J. Durán (comisario), Georges Ifrah, La vida de los números (catálogo de la exposición en la Biblioteca Nacional, junio-septiembre 2006), T ediciones, 2006.
Marc-Alain Ouaknin, El misterio de las cifras, Ma non troppo (de Ediciones Robinbook), 2006.
Howard W. Eves, Mathematical Circles, volume II, The Mathematical Association of America, 2003.
Este artículo es una versión moderna del artículo “La teoría del powerpoint: números y ángulos” (R. Ibáñez), en el portal www.divulgamat.net
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

OSCAR DIEGO
MUY BUENA TEORIA,
DIEGO OSCAR
¿Cual de las 6? ^^
Raúl Ibáñez
¿Cual de las teorías fantásticas te gusta más? 🙂
Teorías fantásticas sobre el origen de la grafía de las cifras
[…] Teorías fantásticas sobre el origen de la grafía de las cifras […]
Teorías fantásticas sobre el orig…
[…] Recientemente alguien me ha recordado en twitter un “famoso” powerpoint que circuló hace algunos años por la red, y que fue enviado masivamente a través del correo electrónico (a mí me llegó varias veces). […]
garxoli del senillar
no lo conocia, muy interesante
María Jesús Fernández Álvarez
Muy interesante. Gracias
Manuel Cruz
Lo que sí que sé, es que el sistema de numeración romano está pensado para minimizar el número de palos (rectilíneos) que hay que trazar para representar el número, probablemente porque tallarlos en hueso o en piedra era un auténtico fastidio, y más si había que hacer una curva. Si probáis alguna vez a resolver un sudoku con la uña me entenderéis.
El origen de la grafía de las cifras | Despejando incógnitas
[…] Escrito por César Tomé. Publicado el 4 de junio de 2014. Extraído de https://culturacientifica.com/2014/06/04/teorias-fantasticas-sobre-el-origen-de-la-grafia-de-las-cifr… […]
Teorías fantásticas sobre el orig…
[…] Recientemente alguien me ha recordado en twitter un “famoso” powerpoint que circuló hace algunos años por la red, y que fue enviado masivamente a través del correo electrónico (a mí me llegó varias veces). El tema del mismo era el origen de la […]
Teorías fantásticas sobre el origen de la grafía de las cifras | El batiburrillo de ideas de sexitante
[…] noticia original […]
Teorías fantásticas sobre el origen de la grafía de las cifras | En un lugar de la mancha
[…] noticia original […]
Teorías fantásticas sobre el origen de la grafía de las cifras | Siempre es viernes
[…] noticia original […]
¿de dónde salieron los números? | Piezas y Elementos
[…] https://culturacientifica.com/2014/06/04/teorias-fantasticas-sobre-el-origen-de-la-grafia-de-las-cifr… […]
5 bulos y leyendas urbanas matemáticas que quizás te has creído » Imaginariums
[…] (s. X) que se conserva en un monasterio de La Rioja. Si quieres saber más, puedes leer el magnífico artículo que Raúl Ibáñez le dedicó en el Cuaderno de Cultura Científica, donde expone otras cinco […]
5 bulos y leyendas urbanas matemáticas que quizás te has creído | Tolomeo
[…] (s. X) que se conserva en un monasterio de La Rioja. Si quieres saber más, puedes leer el magnífico artículo que Raúl Ibáñez le dedicó en el Cuaderno de Cultura Científica, donde expone otras cinco […]
Eufemio
Pues lo del powerpoint ese a mí me lo enseñaron, como algo anecdótico, en la EGB allá por los ochenta. Pero a la edad que lo escuché ví que tenía sentido y siempre lo he tenido como cierto.
La verdad que cuando empiezas a ver el resto de hipótesis me viene a la cabeza la forma en que fueron calzando a posteriori distintos sucesos en las profecías de Nostradamus.
Gracias por la información.
Alejandro Gómez Arangua
Hace muchos años pregunto,sin respuestas lógicas ¿ a quién se le ocurrió ponerle una raya central al N° 7? no lo tiene en los teclados antiguos o nuevos,tampoco en la tipografía gráfica,¿podrían explicármelo? he revisado la numerología arcaica y no lleva cinturón,en la enseñanza sajona,te hacen escribir el 7 como lo conozco,sospecho que viene de España.
El origen de las cifras – El blog de mates
[…] https://culturacientifica.com/2014/06/04/teorias-fantasticas-sobre-el-origen-de-la-grafia-de-las-cifr…; […]
Los números deben de estar locos – Cuaderno de Cultura Científica
[…] (4 = 1 + 1 + 1 + 1, 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1). Como ya mencionamos en la entrada anterior “Teorías fantásticas sobre el origen de la grafía de los números”, los sistemas de numeración más antiguos representaban los números como una acumulación de […]
Victor
Exelente informacion,la unica pagina que me dio exactamente lo que estaba buscando
– Futuro Imperfecto #7: Lo que no te contarán los medios
[…] ¿Números y ángulos? Es lo que intentaron colarnos con un power point varias veces en pleno siglo XXI. […]
Luciano Sánchez del Águila
Muy bién. Me ha gustado mucho.
Raúl Ibáñez – Naukas Bilbao 2019: Teorías fantásticas sobre las grafías de los números — Cuaderno de Cultura Científica
[…] Las grafías de los números son la forma básica y reconocible que tienen los números que usamos hoy, independientemente de la tipografía que empleemos para escribirlos. Es lo que hace que identifiquemos a un cinco como un cinco y a un siete como un siete. Su historia es un recorrido espacio-temporal por la historia de las matemáticas. Y, sin embargo, en webs, libros de divulgación e incluso libros de texto aparecen explicaciones de su origen que nos hablan más del éxito de las fake news y de la falta de rigor a la hora de incorporar información, que de la realidad sobre esa historia misma, ya fascinante de por sí. Raúl Ibáñez pone las cosas en su sitio en este vídeo. Para más detalle puede leerse Teorías fantásticas sobre el origen de la grafía de las cifras. […]
Robert Casas
Muy interesante. Nunca antes me había puesto a pensar en cómo se había construido el origen de los números que hoy conocemos y usamos
La evolución del simbolismo matemático — Cuaderno de Cultura Científica
[…] Teorías fantásticas sobre el origen de la grafía de las cifras […]
Rogelio Renteral Elvira
Realmente me parecen extraordinarias la primera y la quinta, vivimos en un universo ordenado matemáticamente y perfecto, me fascinan estos temas tan interesantes, muchas gracias por su aporte, bendiciones.