Tendemos a pensar en las palabras ciencia o arte como categorías claramente diferenciadas y más o menos constantes a lo largo de la historia. Nada más lejos de la realidad. No sólo los elementos que dichas categorías contienen han cambiado fundamentalmente en distintas épocas (nadie duda que los objetos de arte románico sean distintos a los impresionistas, por ejemplo). Además, los mismos conceptos han cambiado fundamentalmente a lo largo de la historia, adquiriendo incluso significados contradictorios entre sí¹ y aunando actividades creativas que hoy consideramos claramente separadas.

De hecho, el concepto de arte que hoy manejamos no existió hasta el siglo XVIII aproximadamente. Fue en 1746, cuando el filósofo Charles Batteux acuñó el término “bellas artes” agrupando, aproximadamente², las disciplinas que hoy consideramos como tales. El número 7 no era casual, pero hasta cierto punto sí arbitrario: coincidía con el de las 7 artes liberales listadas por los clásicos. Desde entonces, uno de los problemas de la Estética ha consistido en buscar el elemento definitorio de dichas disciplinas, la relación particular que las une entre sí. No es un problema fácil, pero sí muy reciente: hasta hace muy poco, no se pensaba que existiese una vinculación especial entre la música y la pintura, por ejemplo — en rigor, ambas requieren técnicas diferentes, conocimientos diferentes, incluso formas de fruición muy distintas.

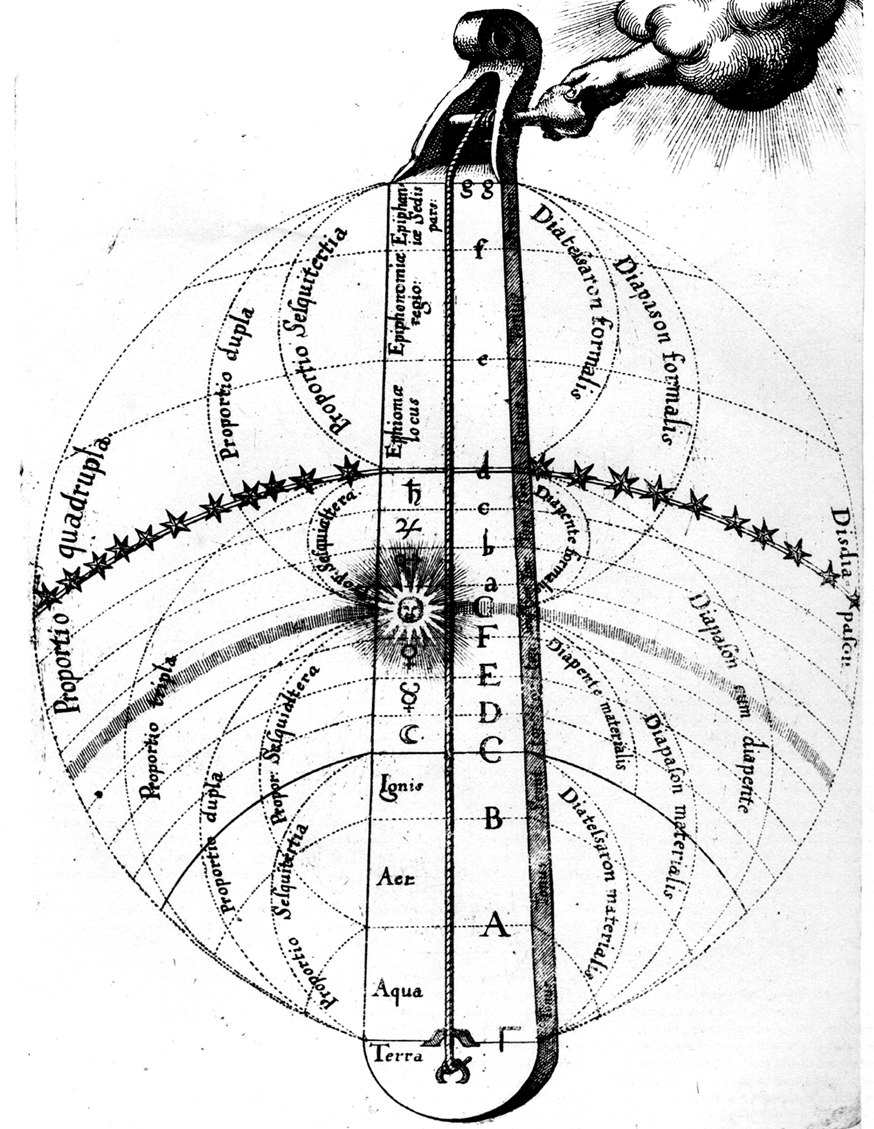
De hecho, hasta la modernidad, la música tendía a agruparse con disciplinas que hoy consideraríamos claramente científicas. Dentro de las artes liberales (aquellas propias de los hombres libres, que no requerían trabajo manual), la música formaba parte del quadrivium, junto con la aritmética, la geometría y la astronomía³. Esto fue así desde la antigüedad clásica: para los griegos, la música representaba la unión entre el mundo idealizado de las matemáticas y el mundo físico de la experiencia, la bisagra perceptible entre la aritmética y la geometría. Gracias a la música, los griegos podían comprobar que dos cuerdas proporcionadas por números enteros sencillos (propios de la aritmética) generaban un sonido agradable o consonante al combinarse. Mientras que cuerdas proporcionadas por números más extraños, con decimales, o bien números irracionales propios del ámbito de la geometría, resultaban en sonoridades desagradables o disonantes. Existe un motivo físico y fisiológico para este fenómeno. Pero, sin conocerlo, los griegos concluyeron que la belleza musical debía emanar de la perfección misma de los números.

Esta misma idea se encuentra tras otro concepto astronómico de origen griego: “cosmos”. El cosmos es un todo ordenado y armónico. Y, por lo tanto, bello (de ahí la palabra “cosmética”). La idea de un universo perfecto, regido por números y armónico (otro concepto muy musical) encuentra su justificación última en nociones musicales. De hecho, el mito pitagórico habla de “la música de las esferas”, una música perfecta aunque no perceptible para nuestros sentidos.

Esta concepción tuvo implicaciones más allá de la anécdota mitológica. El quadrivium formó parte de la educación de las élites durante toda la Edad Media en Europa. Esto significa que gran parte de los grandes pensadores, protocientíficos y filósofos occidentales estudiaron de manera conjunta la astronomía, las matemáticas y la música. Hoy conocemos a Ptolomeo como astrónomo, a Nicolás de Oresme como matemático, a Kepler como físico. Pero hay algo que todos ellos tienen en común: y es que escribieron sobre música. Ptolomeo, en concreto, fue el autor del tratado más importante de teoría musical de la Antigüedad clásica titulado, precisamente “Armónicos”. Nicolás de Oresme reflexionó sobre la conmensurabilidad de las órbitas estelares valorando, entre otras cuestiones, el interés de la música planetaria resultante. Muchos otros autores —Galileo, Newton, Descartes, Euler…⁴— nos dejaron curiosas resonancias musicales en sus trabajos. Pero, sin duda, uno de los casos más interesantes es el de Kepler.

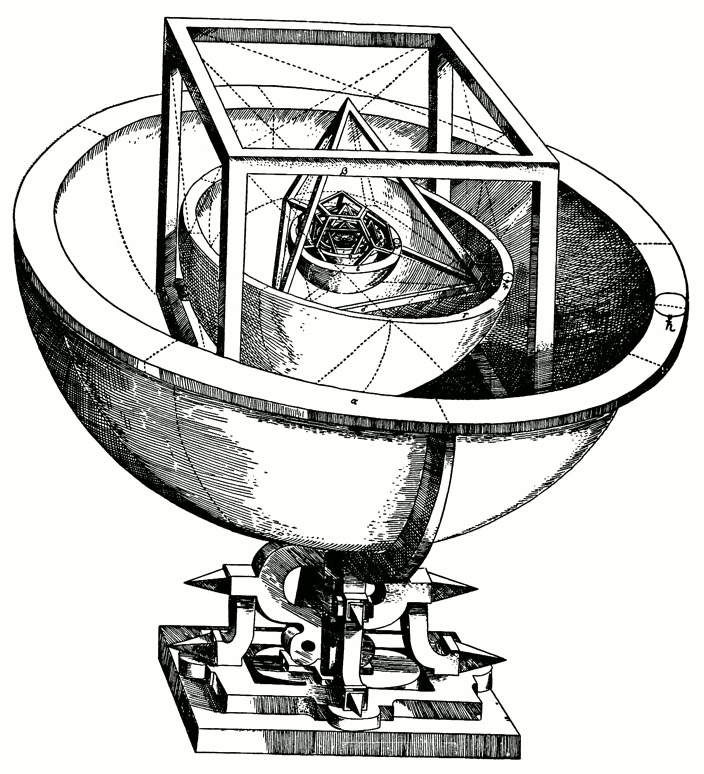
Kepler es conocido por desvelar la forma elíptica de las órbitas planetarias. Fue también el primero en hallar la relación entre el periodo orbital y la distancia al sol. Además, describió cómo la velocidad de cada planeta variaba a lo largo de su elipse. Lo que no resulta tan conocido es que Kepler, en su tratado “Harmonices mundi” además de describir estas leyes astronómicas, asignó notas musicales a cada planeta en función de su velocidad angular. Los planetas con una órbita más excéntrica (por tanto, los planetas cuya velocidad angular es más variable) abarcaban un mayor rango sonoro. Mientras que Venus, por ejemplo, adscrito casi a una circunferencia en su recorrido alrededor del sol, entona siempre la misma nota. Además, Kepler asignó voces a cada uno de ellos: desde Mercurio, la soprano, el planeta más cercano al sol y, por tanto, el de mayor frecuencia (el más veloz), hasta los bajos: Júpiter y Saturno (los más lentos y graves).

Podéis escuchar la música celestial kepleriana en este enlace y comprobaréis que de “celestial” no tiene mucho. Kepler mismo se dio cuenta de que, según su propia teoría, los planetas estarían en disonancia la mayor parte del tiempo, pero argumentó que en determinados momentos, algunos se alinearían produciendo consonancias parciales. Como esta armonía transitoria nunca alcanzaría a los 6 planetas simultáneamente, además, Kepler argumentó que el universo no tendría fin. Tengamos en cuenta que esta era una idea herética para su época, un tiempo en la que la Iglesia Católica hablaba de Apocalipsis y de una Creación finita. A pesar de ello, Kepler daba tanta importancia a la belleza en su teoría que, literalmente, creía que el mundo no podía acabar hasta que sonase bien.

Hoy sabemos que no hay música en las esferas. En el espacio hay vacío, no existe ningún medio por el que puedan viajar las ondas sonoras, ni consonantes ni disonantes. Sin embargo, aunque hayamos descartado la idea de una música celestial, la expectativa de belleza sigue muy presente. La misma belleza con la que Einstein decía poner a prueba sus teorías. La misma belleza cultivada por músicos y artistas. La misma que decía temer Andrei Linde, este año, al conocer los datos experimentales que parecían avalar sus teorías sobre la inflación cósmica.

Probablemente, al final del día, es esta la razón que a muchos nos anima a seguir estudiando o investigando, buscando orden en la enésima ecuación con caracteres griegos: la esperanza de que al final todo encaje, sea elegante y comprensible. Las ganas de poder decir ¡qué bonito!

Notas:

Este post ha sido realizado por Almudena M. Castro (@puratura) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.