 El químico Frederick Soddy (1877-1956) nació un 2 de septiembre.
El químico Frederick Soddy (1877-1956) nació un 2 de septiembre.
Fue Premio Nobel de Química en 1921 por sus contribuciones al conocimiento de la química de las sustancias radiactivas y sus investigaciones sobre el origen y la naturaleza de los isótopos.
Soddy no se dedicó únicamente a la química; las matemáticas, la economía e incluso la poesía fueron otros de sus intereses, entregándose a ellos con bastante acierto.
Uno de los problemas matemáticos que abordó fue el llamado teorema de los círculos de Descartes que establece la relación entre los radios de cuatro círculos tangentes entre sí.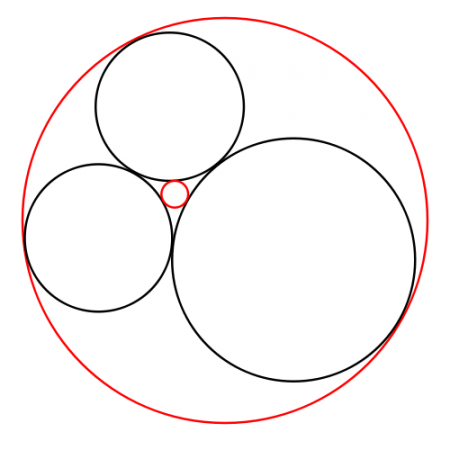
El teorema afirma que si tres círculos son tangentes exteriormente dos a dos (los tres negros de la figura), entonces existen otros dos círculos tangentes a esos tres, uno de ellos interiormente y el otro exteriormente (los dos rojos).
Además, si r1, r2 y r3 son los radios de los tres primeros círculos y r4 es el radio de cualquiera de los dos obtenidos, se obtiene la siguiente relación entre estos cuatro valores:
Soddy publicó su solución en la revista Nature el 20 de junio de 1936 (ver [4]) de una original manera, mediante el poema The Kiss Precise que se transcribe debajo (traducción extraída de [1]).
El beso preciso
Pueden besarse los labios, dos a dos,
sin mucho calcular, sin trigonometría;
mas ¡ay! no sucede igual en geometría,
pues si cuatro círculos tangentes quieren ser
y besar cada uno a los otros tres,
para lograrlo habrán de estar los cuatro
o tres dentro de uno, o alguno
por otros tres a coro rodeado.
De estar uno entre tres, el caso es evidente
pues son todos besados desde afuera.
Y el caso tres en uno no es quimera,
al ser éste uno por tres veces besado internamente.
Cuatro círculos llegaron a besarse,
cuanto menores tanto más curvados,
y es su curvatura tan sólo la inversa
de la distancia desde el centro.
Aunque este enigma a Euclides asombrara,
ninguna regla empírica es necesaria:
al ser las rectas de nula curvatura
y ser las curvas cóncavas tomadas negativas,
la suma de cuadrados de las cuatro curvaturas
es igual a un medio del cuadrado de su suma.
Espiar de las esferas
los enredos amorosos
pudiérale al inquisidor
requerir cálculos tediosos,
pues siendo las esferas más corridas,
a más de un par de pares
una quinta entra en la movida.
Empero, siendo signos y ceros como antes
para besar cada una a las otras cuatro,
el cuadrado de la suma de las cinco curvaturas
ha de ser triple de la suma de sus cuadrados.
El teorema de Soddy está escrito en términos de curvaturas (‘y es su curvatura tan sólo la inversa de la distancia desde el centro’, como explica en sus versos):
Esta relación proporciona dos posibles valores para la curvatura, es decir, hay dos posibles círculos que besan –interna o externamente– a los tres dados inicialmente.
En la última parte del poema, Soddy generaliza el teorema de los círculos de Descartes a dimensión tres. En este caso, dadas dos esferas tangentes entre sí e inscritas en otra gran esfera, se trata de determinar el número de ‘perlas’ que forman el collar de esferas –esferas de distintos tamaños tangentes a sus dos vecinas más próximas y a las tres esferas dadas–. También se busca encontrar la relación entre los radios de las esferas involucradas. El sexteto de Soddy es la solución, es decir, el collar consta de seis esferas, y además, en el poema, Soddy establece la relación entre sus curvaturas:
En el artículo [5], Soddy prueba que es posible encontrar el sexteto de esferas para cualquier elección de tres esferas en las condiciones indicadas inicialmente.
En 1937, el abogado aficionado a las matemáticas Thorold Gosset publicaba en Nature (ver [2]) su propio poema generalizando el resultado de Soddy a espacios n-dimensionales (traducción extraída de [1]):
No debemos empero confinar nuestros cuidados
a los simples círculos, esferas y planos,
sino elevarnos a n-espacios e hipercurvaturas
donde también las múltiples tangencias son seguras.
En n-espacios, los pares de tangentes
son hiperesferas, y es verdad,
–mas no evidente–,
cuando n + 2 de tales se osculean
cada una con n + 1 compañeras
que el cuadrado de la suma de todas las curvaturas
es n veces la suma de sus cuadrados.
Más información:
[1] Martin Gardner, Circo Matemático, 1979 (capítulo 3: Esferas e hiperesferas, edición online preparada por Patricio Barros)
[2] Thorold Gosset, The Kiss Precise, Nature 139 (1937) 62
[3] Marta Macho Stadler, El beso preciso del químico Frederick Soddy, ::ZTFNews, 2014
[4] Frederick Soddy, The Kiss Precise,Nature 137 (1936) 1021
[5] Frederick Soddy, The bowl of integers and the hexlet, Nature 139 (1937) 77-79
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
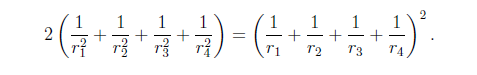
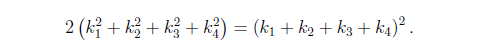
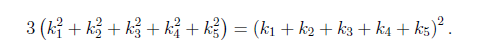

Lo Mejor de la Semana (30 de agosto – 5 de septiembre) | Hablando de Ciencia | Artículos
[…] La ‘química’ entre círculos (y esferas). El premio Nobel de Química de 1921, Frederick Soddy, también se dedicó a las matemáticas y a la poesía, y llegó a combinar ambas de forma muy original. […]