El detective Hercules Poiroti y el inspector Auguste Dupinii llegan a la isla O’Seven; desde hace un año no se sabe nada de los únicos habitantes del castillo allí levantado: James Bondiiiy su mayordomo Stevens.
Una de las torres del fortín está completamente destruida, entre los escombros encuentran los cadáveres de Bond y Stevens. En la cocina descubren un cuaderno con los nombres de las personas que habían residido temporalmente en la isla: las ocho mujeres Felicia W., Cynthia M., Georgia B., Diana M., Emily H., Ann L., Betty T. y Helen G.
Poirot las interroga; al haber pasado un año no recuerdan las fechas exactas de su estancia en la isla, aunque no han olvidado a las mujeres con las que allí coincidieron:
-
Felicia dice haber visto a Ann y Emily;
-
Cynthia comenta que se cruzó con Ann, Betty, Diana, Emily y Helen;
-
Georgia compartió la visita con Ann y Helen;
-
Diana vió a Cynthia y Emily;
-
Emily recuerda a Ann, Cynthia, Diana y Felicia;
-
Ann comenta haberse cruzado con Betty, Cynthia, Diana, Emily, Felicia y Georgia;
-
Betty coincidió con Ann, Cynthia y Helen; y
-
Helen recuerda haberse encontrado con Betty, Cynthia y Georgia.
Cada una de ellas sólo estuvo una vez en O’Seven, hecho corroborado por los pescadores de la zona, encargados de transportar personas y víveres a la isla.
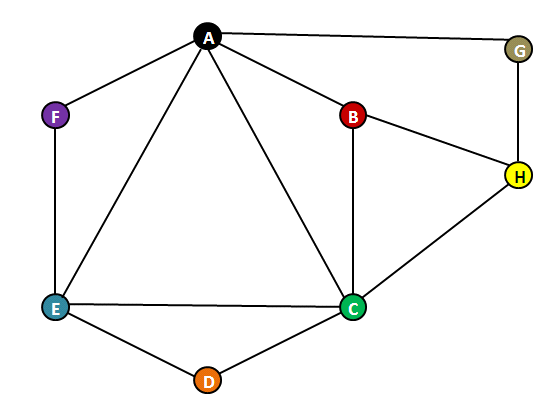
Tras los interrogatorios, Poirot concluye que el asesino es Stevens, muerto accidentalmente. En efecto, la confección de la bomba requería largos preparativos, parecía haber sido una acción individual y sólo el mayordomo poseía las llaves del ala del castillo en la que se había producido la explosión. Sin embargo, el inspector Dupin no coincide con Poirot, y afirma conocer la identidad de la culpable, basándose en sus conocimientos matemáticos. El inspector muestra a Poirot un grafo en el que cada vértice corresponde a una de las mujeres (los etiqueta con la inicial del nombre de cada mujer, A por Ann, B por Betty, etc.) y en el que dos vértices están unidos por una arista si las dos mujeres recuerdan haberse encontrado en la isla.
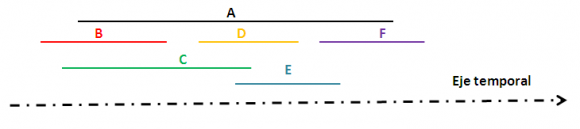
Suponiendo que ninguna de las mujeres miente, Dupin explica que su presencia en la isla se puede representar mediante intervalos dibujados sobre un eje temporal: si dos intervalos se superponen, esas dos mujeres se han encontrado. El grafo dibujado es el grafo de intervalos representando las estancias de las ocho mujeres: cada vértice corresponde a un intervalo de tiempo (el tiempo que permaneció en la isla la mujer etiquetada) y una arista une dos vértices si los correspondientes intervalos temporales se cruzan.
Dupin comenta a Poirot que este tipo de grafos fueron introducidos por el matemático György Hajós en 1957 y que, para averiguar la verdad, se ha basadoiv en dos de sus propiedades:
Propiedad 1: Todo grafo de intervalos está triangulado, es decir, cada camino cerrado (camino de aristas que empieza y termina en el mismo vértice) de longitud mayor o igual que cuatro contiene al menos una cuerda (arista que une dos vértices de ese camino, pero que no forma parte de él).
Propiedad 2: En un grafo de intervalos no puede haber un triangulo inscrito en un hexágono.
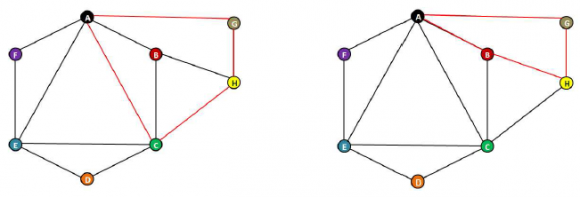
Y Dupin continúa razonando de este modo: en su grafo existen dos cuadriláteros que contradicen la propiedad 1: ACHG y ABHG.
Mirando, por ejemplo, el segundo, pensemos en los intervalos temporales que representan: si han coincidido A y B, B y H, H y G y A y G, necesariamente, B y G también han tenido que coincidir en la isla:
Es decir, el grafo debería tener una arista uniendo B y G, arista que no existe según las declaraciones.
Así, si los cuadriláteros ACHG y ABHG no son posibles, y se concluye que alguna de las mujeres ha falseado su declaración, es decir, alguna entre Ann, Cynthia, Helen o Georgia (para ACHG) miente y alguna entre Ann, Betty, Helen o Georgia (para ABHG) no ha dicho la verdad. Como sólo hay una culpable, la mentirosa debe encontrarse entre Ann, Helen o Georgia.
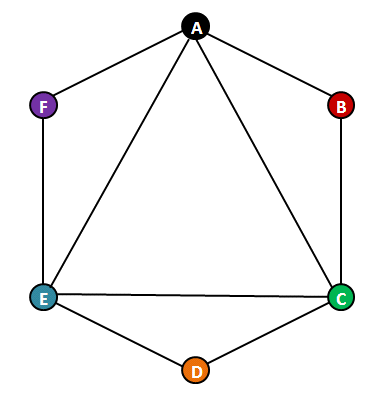
Dupin alude a continuación a la propiedad 2; en su grafo sólo hay un hexágono: ABCDEF, y posee un triángulo inscrito. ¿Por qué no es posible?
Analizando este subgrafo en términos de intervalos de tiempo, se ve que si Ann, Betty, Cynthia, Diana, Emily y Felicia han coincido (según ellas confiesan), necesariamente Ann y Diana también han tenido que coincidir en la isla.
Es decir, falta una arista entre A y D, y por lo tanto, una de estas mujeres ha mentido: Ann, Betty, Cynthia, Diana, Emily o Felicia.
Finalmente, teniendo en cuenta los dos listados de nombres extraídos al aplicar las dos propiedades de grafos de intervalos, Dupin deduce que Ann es, sin ninguna duda, la culpable.
En su declaración, Ann dice haber visto a Diana (pero Diana no habla de haber coincidido con ella, por eso Dupin no traza la arista entre los vértices A y D) y Ann miente al decir que no ha visto a Helen (aunque es cierto que Helen no ha visto a Ann): en ambos casos la asesina debía estar escondida preparando su perverso plan…
i Descendiente del célebre detective del mismo nombre, protagonista de las novelas de Agatha Christie.
ii Descendiente del célebre detective del mismo nombre, protagonista de tres novelas de Edgar Allan Poe. El inspector Dupin había estudiado matemáticas en Oxford.
iii Un vividor, descendiente del célebre espía del mismo nombre, protagonista de las novelas de Ian Fleming.
iv Dupin está realizando una tesis doctoral sobre grafos de intervalos, por eso sabe tanto sobre ellos.
Nota 1: Este texto es una adaptación de la reseña Qui a tué le duc de Densmore ?de Claude Berge aparecida en la sección de Literatura y Matemáticas (enero de 2015) de DivulgaMAT.
Nota 2: Esta entrada participa en la edición5.X: Sofia Kovalévskaya del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.


Incidente en la isla O’Seven | Mi Caj&oac…
[…] El detective Hercules Poiroti y el inspector Auguste Dupinii llegan a la isla O’Seven; desde hace un año no se sabe nada de los únicos habitantes del castillo allí levantado: James Bondiiiy su mayordomo Stevens. Una de las torres del fortín […]
Carnaval de Matemáticas: resumen de la Edición 5.X (Sofia Kovalévskaya) | :: ZTFNews.org
[…] 3: Incidente en la isla O’Seven de @MartaMachoS desde el blog Cuaderno de Cultura […]
Incidente en la isla O’Seven
[…] Incidente en la isla O’Seven […]
Edición 5.X del Carnaval de Matemáticas: ‘And the winner is…’ | :: ZTFNews.org
[…] 3: Incidente en la isla O’Seven de @MartaMachoS desde el blog Cuaderno de Cultura Científica, con 10 puntos […]