Imagino que muchas de las personas que estáis leyendo esta entrada de la sección Matemoción del Cuaderno de Cultura Científica, conoceréis alguna de las versiones de un rompecabezas de ingenio llamado Locura instantánea, aunque también ha recibido otros muchos nombres. Yo tengo la versión en madera que aparece en la imagen siguiente.

El rompecabezas consta de cuatro cubos, cada una de cuyas caras está coloreada con uno de los cuatro colores del juego (en la imagen, rojo, azul, verde y amarillo), siguiendo un patrón determinado. Hay diferentes patrones, la mayoría son esencialmente el que aparece en la imagen siguiente con los cuatro cubos desplegados. El objetivo del solitario es colocar los cuatro cubos, uno encima (o a continuación) del otro, formando una torre (o un prisma rectangular de tamaño 1 x 1 x 4) de manera que cada uno de los cuatro colores aparece una vez, y por lo tanto, solo una, en cada una de las cuatro caras de la torre.

Este es un interesante juego, aunque mi entrada de hoy no estará centrada en el mismo, sino en algo que descubrí relacionado con él.

Hace unas semanas me encontraba yo escribiendo sobre la conocida demostración por medio de grafos de la solución del Cubo 4, y se citaba como origen de la misma el artículo “The colored cubes problem” (Eureka, 1947) de F. de Carteblanche. Al buscar información sobre este matemático, resultó lo siguiente. En Google aparecían un montón de referencias a la expresión, que deriva del francés, “carte blanche”, y que significa “carta blanca” (utilizada como “dar carta blanca a alguien”), pero nada sobre él. Rápidamente al centrarnos en las entradas matemáticas –escribiendo la expresión “math” en google-, apareció el artículo On the Tantalizer and Instant insanity (Historia Mathematica, 1977) de Frank Harary, en el que se explicaba que F. de Canterblanche era el marido de la matemática Blanche Descartes, pero que en realidad ambos eran seudónimos de un grupo de cuatro estudiantes de Cambridge, que los habían utilizado para publicar “poemas y notas matemáticas para entretener”.

Sin lugar a dudas el seudónimo más famoso dentro de las matemáticas es el de Nicolás Bourbaki, del que podéis leer en la entrada de Marta Macho, Nicolás Bourbaki, el matemático que nunca existió. Sin embargo, aunque existen más casos, estos no suelen ser tan conocidos.

¿Quién, o qué, es Blanche Descartes? En el artículo The story of Blanche Descartes se cuenta como tres jóvenes estudiantes de Matemáticas del Trinity College de Cambridge, en su primer año, Cedric Smith, Arthur Stone y Leonard Brooks, y un estudiante de Químicas pero un apasionado de las matemáticas, William Tutte, se conocieron y se hicieron amigos, compartiendo su pasión por los problemas matemáticos.

Los “cuatro del Trinity”, como en ocasiones se les llamaba, empezaron a compartir problemas matemáticos e intentar resolverlos. Uno de los primeros en los que empezaron a trabajar fue la “cuadratura de un cuadrado”. Arthur les había comentado a sus amigos que existía la conjetura de que era imposible dividir un cuadrado en cuadrados de diferentes tamaños, y empezaron a trabajar en ella.

Se conocía que un rectángulo sí podía ser cuadrado con baldosas cuadradas de diferentes tamaños. El primer ejemplo fue de Zbigniew Morón en 1925, con diez baldosas cuadradas. En los primeros intentos de los cuatro del Trinity por resolver el problema, encontraron varios rectángulos divididos en cuadrados, pero no un cuadrado. Tras tres años peleándose con el problema consiguieron dividir finalmente un cuadrado en 69 cuadrados más pequeños, todos ellos diferentes. Además, lo aplicaron a los circuitos eléctricos. Sus resultados sobre la disección de rectángulos en cuadrados los recogerían en el artículo The dissection of rectangles into squares (Duke Math. J., 1940), firmado con sus propios nombres.

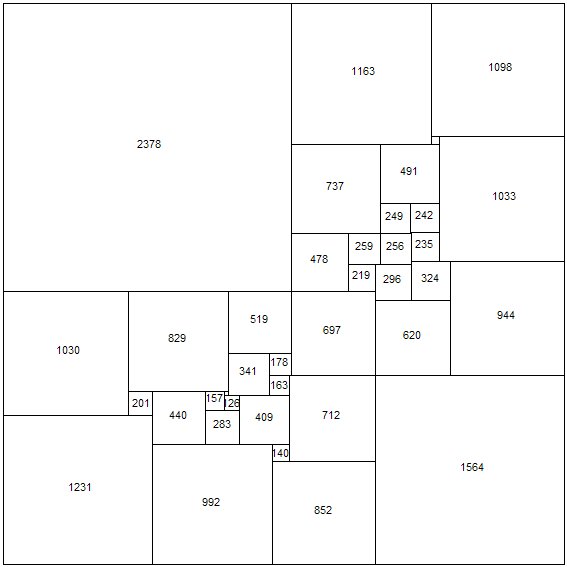
Posteriormente, descubrirían que se les había adelantado el matemático alemán Roland Sprague (1894-1967), quien en 1939 publicó (en alemán) un ejemplo de cuadratura de un cuadrado con 55 baldosas cuadradas distintas, en la revista Math. Z.

Así mismo, descubrieron lo que se conoce como la Disección de Blanche, que consistía en dividir un cuadrado en rectángulos de igual área, pero diferentes dimensiones.

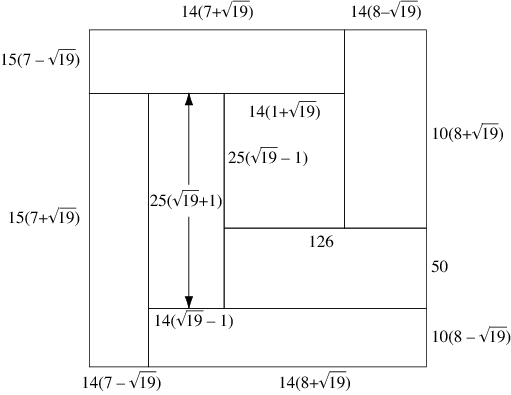
Pero, ¿de dónde surge el nombre de Blanche Descartes con el que escribirían unos treinta trabajos, incluidos artículos de matemáticas serias? Uno de los cuatro del Trinity, Cedric, conoció directamente de uno de los implicados el caso de un grupo de matemáticos que había publicado un artículo humorístico sobre formas matemáticas de atrapar un león en el desierto, y que lo habían firmado con un seudónimo Hector Pétard. Los dos primeros métodos son:

Método 1 (de Hilbert, o axiomático): Coloquemos una jaula cerrada en el desierto. Y utilicemos el siguiente sistema axiomático:

AXIOMA 1: El conjunto de los leones es no vacío.

AXIOMA 2: Si existe un león en el desierto, el león existe en una jaula.

TEOREMA 1: Existe un león en la jaula.

Método 2 (por inversión): Colocamos una jaula esférica cerrada en el desierto, vacía de leones y entremos. Realizamos una inversión con respecto a la jaula. Esta función manda al león dentro de la jaula, y a nosotros, fuera.

El caso del matemático Hector Pétard les animó a elegir un seudónimo para el grupo de los cuatro del Trinity.

Tomando las primeras letras de sus nombres (Bill, Leonard, Arthur y Cedric) obtuvieron BLAC. Una de las ideas fue utilizar el seudónimo “El reverendo Cornelius Black”, utilizando la similitud de BLAC con la palabra black (el color negro), pero Brooks no estaba de acuerdo. Decidieron cambiar del color negro (black) al blanco (BLAnChe), de la expresión “carte blanche”, y el apellido elegido para la matemática fue Descartes, en honor al matemático y filósofo francés René Descartes (1596-1650). El nombre estaba fijado, Blanche Descartes. Y además, Blanche tenía un marido, Filet de Carteblanche. Bajo estos seudónimos publicaron sobre una treintena de trabajos, desde poemas y humor matemático, hasta artículos matemáticos en campos como el coloreado de grafos o las teselaciones, y también sobre juegos y problemas matemáticos.

¿Quiénes eran las cuatro personas que se escondían detrás del nombre de Blanche Descartes, y en menor medida, de su marido Carteblanche?

Leonard Brooks (1916-1993). Se convertiría en inspector de hacienda, pero su interés por las matemáticas continuó vivo. Demostró un teorema que lleva su nombre, Teorema de Brooks, que establece una relación entre el grafo de un grafo y su número cromático.

Arthur Stone (1916-2000). Trabajó fundamentalmente en Topología. Realizó su tesis doctoral en Princeton bajo la supervisión del gran topólogo estadounidense Solomon Lefschetz (1884-1972). Durante su estancia en Estados Unidos, durante los años de la Segunda Guerra MUndial, trabajó también con el matemático húngaro Paul Erdös (1913-1996), y demostraron el conocido como Teorema de Erdös-Stone de Teoría de Grafos. Así mismo, de esa época (1939) es su descubrimiento del primer flexágono, un trihexaflexágono. Y el teorema de metrización de Stone se llama así debido a este matemático. Las universidades en las que estuvo de profesor fueron Cambridge, Manchester, Rochester y Northeastern en Boston.

Cedric Smith (1917-2002). Sus campos de trabajo fueron la estadística y la genética. Durante la Segunda Guerra Mundial, como cuáquero y objetor de conciencia trabajaría en un hospital de Cambridge. Tras la guerra entraría a trabajar en el Laboratorio Galton, la unidad de genética humana del Colegio Universitario de Londres, donde desarrollaría algunos métodos matemáticos utilizados para realizar el mapa genético humano. La S del Teorema BEST (BEST Theorem en inglés) de la Teoría de Grafos se debe a él.

Bill Tutte (1917-2002). A pesar de sus inicios estudiando Químicas, Tutte acabaría siendo un reconocido matemático y criptógrafo. Durante la segunda guerra mundial formaría parte del grupo de científicos que trabajaría en Bletchley Park para descifrar los códigos alemanes, como también estuvo Alan Turing (1912-1954). Bill Tutte, junto con el militar de inteligencia John Tiltman, consiguieron descifrar la “cifra Lorenz”, que era la que utilizaban los alemanes en sus comunicaciones entre Hitler y sus generales, lo que les permitió leer los mensajes del Führer, y acortar la guerra.

Después de la Segunda Guerra Mundial se trasladaría a Canada, primero a Toronto, invitado por el matemático inglés afincado en Canada H. S. M. Coxeter (1907-2003), y después en Waterloo (Ontario). Trabajaría fundamentalmente en Teoría de Grafos. Escribió unos 170 artículos y varios libros, entre ellos, Connectivity in graphs (1966), Introduction to the theory of matroids (1971), Graph Theory (1984), y Graph Theory as I Have Known It (1998).

El último artículo que publicarían los cuatro juntos, con sus nombres, fue Determinants and current flows in electric networks (Discrete Math. 100, 1992).

Algunas de las publicaciones de Blanche Descartes fueron:

– A Three color problem, Eureka 9, pp. 21, 1947. [en el mismo número que su marido publicó el artículo sobre el rompecabezas]

– The Twelve Coin Problem, Eureka 13, pp. 7, 1950.

– Why are Series Musical?, Eureka 16, pp. 18-20, 1953.

– Hymne to Hymen (poem), Eureka 17, pp. 5-7, 1954.

– [con su hermana Rose Descartes], La coloration des cartes, Eureka 31, pp. 29-31, 1968.

– Division of a Square into Rectangles, Eureka 34, pp. 31-35, 1971.

– Curious cubes, Eureka 55, pp. 49, 2001-02.

Eureka es la revista de los Arquimedianos, la sociedad matemática de la Universidad de Cambridge, fundada en 1935.

– Network-colourings, The Mathematical Gazette 32, n. 299, pp. 67-69, 1948.

– [con Peter Ungar] Advanced Problems and Solutions: 4526, American Mathematical Monthly 61, n.5, pp. 352-353, 1954.

– Review of Bondy & Murty’s Graph theory with applications, Bulletin of the American Mathematical Society 83, n. 3, pp. 313–315, 1977.

Y de su marido F. de Carteblanche, además del ya citado:

– The princess and the roses, J. Recreac. Math. 3, pp. 238-239, 1970.

– The roses and the princess, J. Recreac. Math. 7, pp. 295-298, 1974.

Bibliografía

1.- F. de Carteblanche, The colored cubes problem, Eureka 9, pp. 9-11, 1947.

2.- Frank Harary, On the Tantalizer and Instant insanity, Historia Mathematica 4, n.2, pp.205-206, 1977.

3.- Marta Macho, Nicolás Bourbaki, el matemático que nunca existió, Cuaderno de Cultura Científica, 2014

4.- Cedric A. B. Smith, Steve Abbott, The story of Blanche Descartes, The Mathematical Gazette 87 (508), pp. 23-33, 2003.

5.- R. L. Brooks, C. A. B. Smith, A. H. Stone, W. T. Tutte, The dissection of rectangles into squares (Duke Math. J., 1940)

6.- La ciencia de la Mula Francis, Humor para matemáticos: 34 maneras de atrapar un león

7.- www.squaring.net, Brooks, Smith, Stone, Tutte (Part I y Part II).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Este post forma parte del Carnaval de Matemáticas, que en esta quincuagésima tercera edición, también denominada 6.3: Teorema de Pitágoras, está organizado por Rafael Martínez González a través de su blog El mundo de Rafalillo.