En mi anterior entrada del Cuaderno de Cultura Científica La cuadratura del cuadrado: en busca del santo grial estuvimos hablando de un hermoso rompecabezas matemático, el problema de la cuadratura perfecta del cuadrado, que recuerdo a continuación:

Problema de la cuadratura perfecta del cuadrado (o rectángulo): Dividir un cuadrado (o rectángulo) en un número finito de cuadrados más pequeños, todos de distintos tamaños.

Este problema, que durante mucho tiempo se pensó que no tenía solución para cuadrados, lo que se conoció como la conjetura de Luzin, fue finalmente resuelto en positivo, alrededor del año 1939, por dos grupos de matemáticos. Por una parte, el matemático alemán Roland P. Sprague (1894-1967) construyó un cuadrado con una cuadratura perfecta, pero compuesta (recordemos que eso significa que contiene la cuadratura de algún sub-rectángulo), de orden 55. Mientras que los cuatro estudiantes del Trinity College de la Universidad de Cambridge (Reino Unido), Rowland L. Brooks (1916-1993), Cedric A. B. Smith (1917-2002), Arthur H. Stone (1916-2000) y William Th. Tutte (1917-2002), consiguieron construir el primer cuadrado perfecto simple (no compuesto), también de orden 55. Para ello, los cuatro de Trinity (puede leerse más sobre ellos en la entrada Blanche Descartes y la cuadratura del cuadrado) relacionaron el problema de las disecciones cuadradas de los rectángulos, en particular, de los cuadrados, con la teoría de las redes eléctricas de Kirchhoff, que es de lo que vamos a hablar en esta entrada.

Como explicamos en la anterior entrada, La cuadratura del cuadrado: en busca del santo grial, el primer acercamiento de los jóvenes estudiantes de Cambridge, Brooks, Smith, Stone y Tutte, fue experimental. Intentaron construir mediante una sencilla técnica algebraica algún ejemplo de disección de un cuadrado en cuadrados más pequeños de diferentes tamaños. Con esta técnica sí consiguieron construir algunos ejemplos de cuadraturas perfectas de rectángulos, pero no de cuadrados. Este método experimental dependía demasiado de la suerte y podrían no encontrar nunca el ansiado grial, una cuadratura perfecta del cuadrado. Era como encontrar una aguja en un pajar, sin saber además si había aguja. Por este motivo, abandonaron el camino experimental a favor de un enfoque más teórico, que además les permitiera conocer más sobre el problema.

Entonces, empezaron a asociar diferentes tipos de diagramas a las cuadraturas de los rectángulos. Hasta que llegaron a un diagrama propuesto por Cedric Smith, que sus compañeros no dudaron en llamar el “diagrama de Smith”, que asociaba cada cuadratura de un rectángulo con el grafo de una red eléctrica.

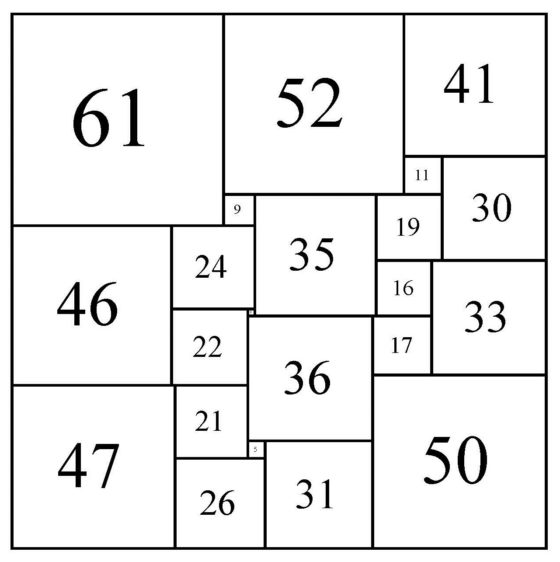
Para ilustrar la construcción de la red eléctrica asociada a una cuadratura, consideraremos el ejemplo de la división de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18, luego de orden 9, obtenida por el matemático polaco Zbigniew Moron en 1925, que aparece en la siguiente imagen. Cada segmento horizontal se representará como un vértice del grafo y dos vértices estarán unidos mediante una arista si existe un cuadrado que tiene su lado superior apoyado en el segmento horizontal correspondiente a uno de los vértices y su lado inferior apoyado en el segmento horizontal del otro vértice. Además, el grafo está dirigido, como se muestra mediante las fechas de las aristas, de arriba hacia abajo, que es el orden de la corriente eléctrica, del polo positivo (que consideramos el vértice del lado horizontal superior) al polo negativo (el vértice del lado horizontal inferior). Más aún, es un grafo etiquetado, ya que asociamos a cada arista el valor del lado del cuadrado correspondiente, que será el valor de la corriente eléctrica.

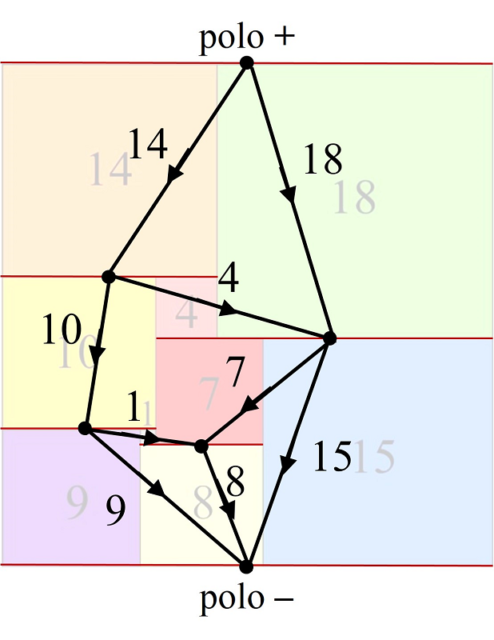
Lo curioso es que el diagrama de Smith cumple las leyes de Kirchhoff para las redes eléctricas, asumiendo que la resistencia de cada arista es igual a 1. La primera ley de Kirchhoff establece que en cada nodo (vértice) del circuito eléctrico, con excepción de los polos, la suma de las corrientes debe ser cero, es decir, la suma de las corrientes que entran en el nodo es igual a la suma de las corrientes que salen del mismo. Por ejemplo, si miramos a la red eléctrica anterior, en el primer vértice después del polo positivo, entra una corriente de 14 y salen dos de 10 y 4, o en el siguiente entran dos corrientes de 4 y 18, mientras que salen dos corrientes de 7 y 15. Esto es debido a que, en un segmento horizontal (vértice) cualquiera de la cuadratura del rectángulo, la suma de los lados de los cuadrados que se apoyan en el segmento desde arriba (la suma de las corrientes que entran) es igual a la suma de los lados de los cuadrados que se apoyan en el segmento desde abajo (la suma de las corrientes que salen), que en ambos casos es la longitud del segmento horizontal.

Teniendo en cuenta que, por la ley de Ohm de los circuitos eléctricos, la diferencia de potencial de cada arista del circuito es igual al producto de la resistencia, que en este caso hemos asumido que es 1, por la corriente, ambas –diferencia de potencia y corriente- son iguales. Por lo tanto, la segunda ley de Kirchhoff establece que la suma algebraica de las corrientes –diferencias de potencial- de cualquier circuito cerrado es cero. En el ejemplo de arriba, en el primer circuito cerrado tenemos que 14 + 4 – 18 = 0 o en el segundo 10 + 1 – 7 – 4 = 0. Esto es debido a que cada segmento vertical de la cuadratura del rectángulo se corresponde con un circuito cerrado, y la suma de las longitudes de los lados de los cuadrados a izquierda y derecha del segmento valen lo mismo, la longitud del segmento vertical.

La corriente que entra en el circuito eléctrico por el polo positivo, que es igual a la que sale por el polo negativo, es la longitud de los lados horizontales del rectángulo. En el ejemplo de arriba, 14 + 18 = 9 + 8 + 15 = 32. Por otra parte, la diferencia de potencial entre los dos polos es igual a la longitud de los lados verticales del rectángulo. De nuevo, en el ejemplo la diferencia de potencial la podemos calcular a través de cualquiera de los recorridos entre el polo positivo y el negativo, 14 + 10 + 9 = 14 + 4 + 7 + 8 = 18 + 15 = 33, entre otros. Por lo tanto, si la corriente que entra por el polo positivo, y sale por el negativo, es igual a la diferencia de potencial, estaríamos ante un circuito eléctrico que se corresponde con la cuadratura del cuadrado.

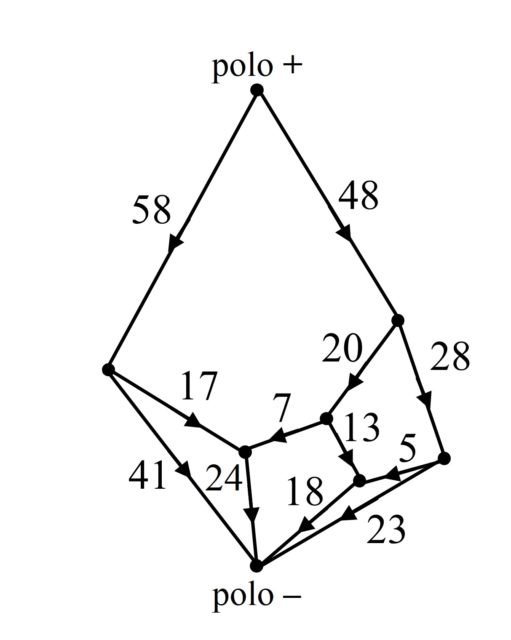
En conclusión, cada cuadratura de un rectángulo se corresponde con una red eléctrica, lo cual les permitió utilizar los conocimientos de la teoría de redes eléctricas para estudiar el problema de la cuadratura de los rectángulos, y del cuadrado. Por ejemplo, en la imagen anterior tenemos una red eléctrica, os dejo como divertimento el construir la cuadratura del rectángulo asociada (solución al final de la entrada).

En particular, esto simplificó el problema de construir y clasificar las cuadraturas perfectas simples de rectángulos. Por ejemplo, analizaron todos los circuitos eléctricos con hasta 11 aristas y construyeron las cuadraturas de rectángulos asociadas. Así probaron que no existen cuadraturas perfectas simples de rectángulos de orden menor que 9, que solo hay dos de orden 9 (mostradas en la anterior entrada La cuadratura del cuadrado: en busca del santo grial, una de ellas es la asociada al primer circuito eléctrico que hemos mostrado más arriba), seis de orden 10 y veintidós de orden 11. Y siguieron clasificando las cuadraturas de orden 12, que hay sesenta y siete, y después de orden 13. Este fue el inicio de una fructífera investigación sobre las cuadraturas perfectas de rectángulos. Pero como veremos, también del cuadrado.

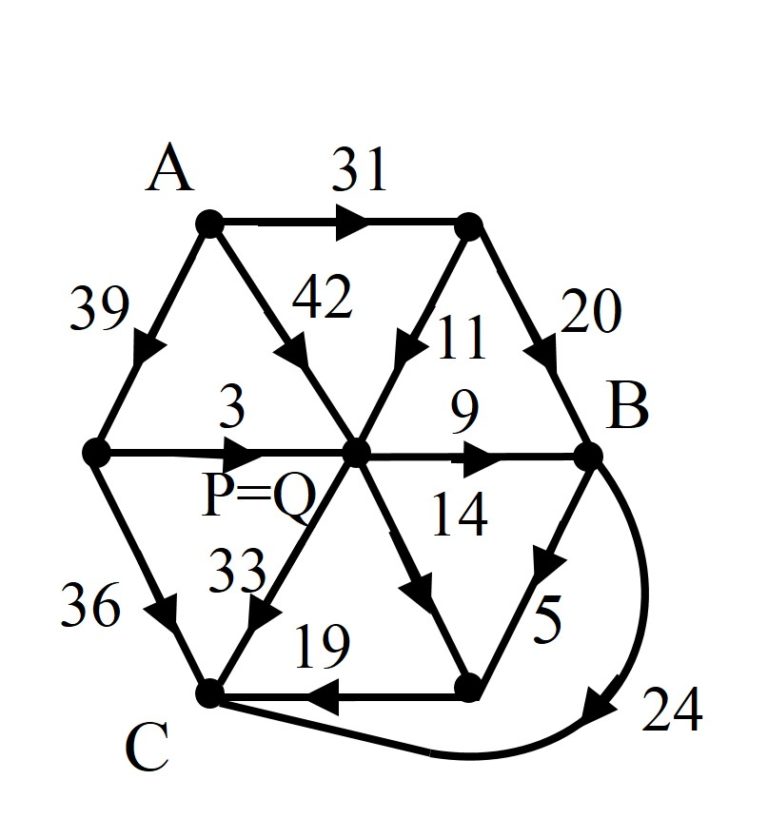
Uno de los estudios que realizaron fue el análisis de redes eléctricas con ciertas simetrías. Por ejemplo, consideraron el circuito eléctrico asociado a un cubo, vértices y aristas, que no proporcionaba cuadraturas perfectas de rectángulos, pero cuando se añadía una de las diagonales de una de las caras del cubo, se obtenía el diagrama de Smith de la siguiente imagen y la correspondiente cuadratura perfecta simple del rectángulo, que se muestra después.

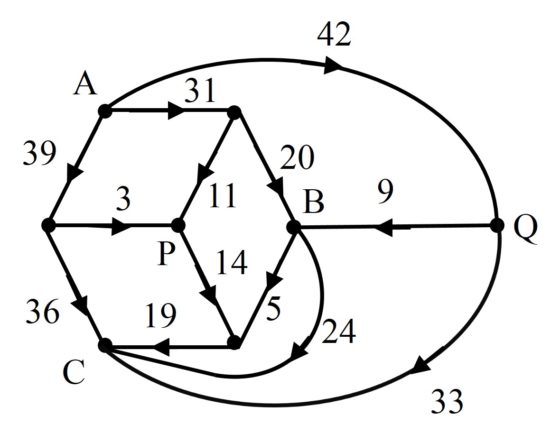
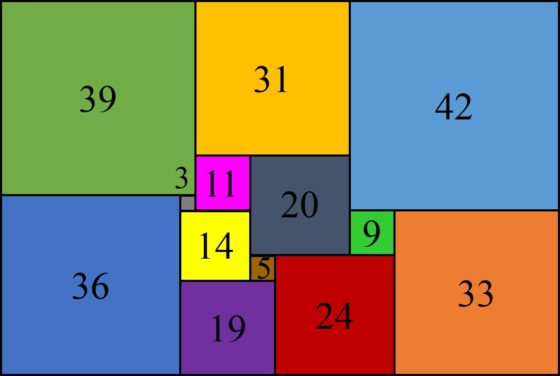
Una bonita historia relacionada con esta cuadratura del rectángulo es la siguiente. Leonhard Brooks estaba tan satisfecho con este ejemplo que decidió construirse un rompecabezas geométrico cuyas piezas eran los cuadrados de la cuadratura del rectángulo anterior, es decir, de lados 3, 5, 9, 11, 14, 19, 20, 24, 31, 33, 36, 39 y 42, con el que jugar a realizar el rectángulo original. Entonces su madre cogió el rompecabezas para jugar con él y consiguió formar el rectángulo con ellas, pero resultó que no era la misma solución anterior, las piezas estaban colocadas de forma diferente. Con la ayuda de la madre de Brooks, habían encontrado dos disecciones perfectas simples del rectángulo 112 x 75 realizadas con los mismos cuadrados.

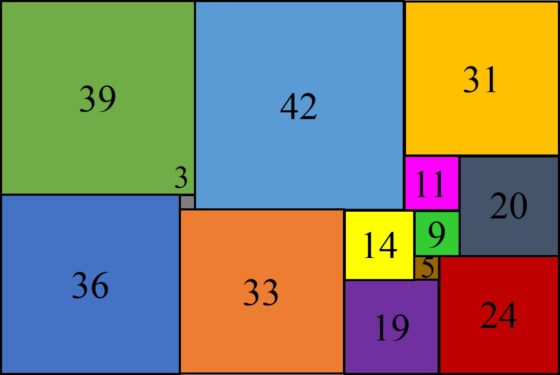
La red eléctrica asociada a esta nueva descomposición perfecta y simple del rectángulo 112 x 75 se puede obtener a partir del primer circuito eléctrico (que está representado arriba) identificando los vértices P y Q, lo cual es posible ya que tienen la misma diferencia de potencial, en concreto, 42.

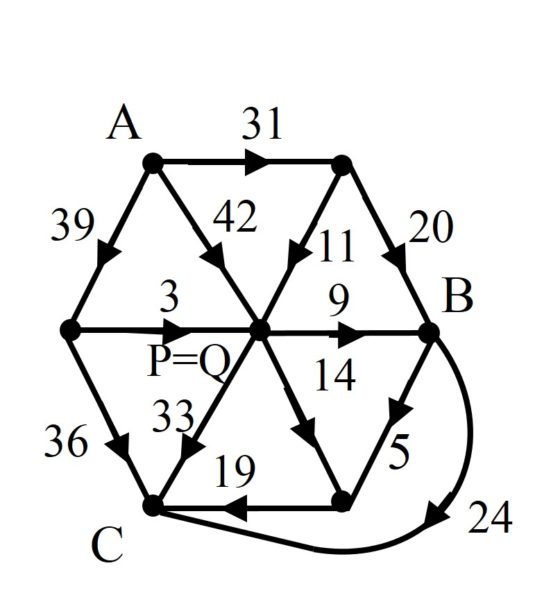
Analizaron el motivo por el cual se producía este fenómeno y tenía que ver con la simetría de algunas redes eléctricas, aunque no entraremos en los detalles técnicos en esta entrada, por este motivo empezaron a analizar circuitos eléctricos en los cuales cogían la red eléctrica anterior, que habían obtenido a partir del cubo, y sustituyeron la parte simétrica central (el hexágono plano que contiene a los vértices A, B, C y centro P) por otras estructuras simétricas. Así consiguieron obtener más ejemplos de dobles cuadraturas perfectas simples de un mismo rectángulo con los mismos cuadrados.

Esta técnica, después de seguir investigando y obtener otros ejemplos, les llevó a encontrar su primer ejemplo de cuadratura perfecta de un cuadrado. La pieza central simétrica tenía la siguiente forma.

La cuadratura perfecta, que era compuesta, que obtuvieron era de orden 39, es decir, formada por 39 cuadrados de diferentes tamaños, que componían un cuadrado de lado 4.639. Utilizando el código de Bouwkamp que explicamos en la anterior entrada, esta era la cuadratura [2.378, 1.163, 1.098], [65, 1.033], [737, 491], [249, 242], [7, 235], [478, 259], [256], [324, 944], [219, 296], [1.030, 829, 519, 697], [620], [341, 178], [163, 712, 1.564], [201, 440, 157, 31], [126, 409], [283], [1231], [992, 140], [852]. Como cada corchete del código de Bouwkamp nos dice qué cuadrados, su lado, están debajo de cada segmento horizontal, de arriba abajo, podemos ver qué cuadratura prefecta del cuadrado, de lado 4.639, habían construido.

Poco después, encontrarían el primer ejemplo de cuadratura perfecta simple de un cuadrado de orden 55, utilizando las mismas técnicas.

Como hemos podido ver, relacionar las cuadraturas perfectas de los rectángulos con redes eléctricas se demostró una técnica muy fructífera en la resolución del problema de la cuadratura del cuadrado, y del rectángulo, y en el estudio general de estas cuestiones.

Y, por cierto, la solución a la cuestión planteada arriba sobre cuál es la cuadratura perfecta asociada a la red eléctrica que habíamos mostrado, es la siguiente.

Bibliografía

1.- Wolfram MathWorld: Perfect Square Dissection.

2.- Stuart Anderson, Tiling by squares.

3.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987. Contiene el capítulo de W. Th. Tutte Squaring the square.

4.- Wikipedia: Kirchhoff’s circuit laws

5.- Arkadiusz Maciuk, Antoni Smoluk, Tiling by squares, Kirchhoff’s Laws and a Flow Problem in the Economy, Didactics of Mathematics, n. 14 (18), 2017.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica