Las mentiras de la propiedad conmutativa
A todos los que hemos ido al colegio en España, nuestro profe de matemáticas nos enseñó que, cuando sumamos y multiplicamos, “el orden de los factores no altera el producto”. Y a nadie se lo ocurrió ponerle en duda. Nos lo aprendimos y con ello vivimos, al menos los que no estudiamos ciencias.
Los que sí se decantaron por las ciencias, descubrieron años después que el maestro no decía toda la verdad. Y es que la propiedad conmutativa es cierta solamente para las sumas y multiplicaciones ‘ordinarias’ lo que hace que sea relevante, por ejemplo en la lógica proposicional y en algunas operaciones de teoría de conjuntos, entre otras.
De esa forma, 2+3=5 lo mismo que 3+2=5 y en el caso de la multiplicación, 2×3=6 igual que 3×2=6 pero fuera del colegio, la realidad es otra porque no sólo es importante el resultado final sino cómo se llega a él.
Y con eso se encontró hace unos meses un estudiante al que su profesora le marcó una respuesta como errónea e internet se encargó que diese la vuelta al mundo:

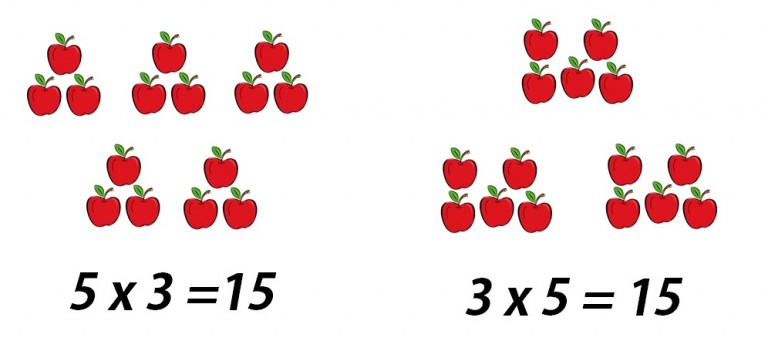
Lo cierto es que el debate se resuelve fácilmente si se atiende a la siguiente explicación: no es lo mismo representar 15 elementos en grupos de 3 que en grupos de 5 y tal y como está planteada la operación en el ejercicio, al alumno se le pide que represente 5 veces el 3 (no tres veces el cinco) o lo que es lo mismo 3+3+3+3+3.
Poniendo un ejemplo real, no se verían igual cinco bolsas con tres manzanas cada una que tres bolsas con cinco manzanas cada una. Aunque en los dos casos tendríamos un total de 15 manzanas, de una forma tendríamos tres bolsas y de la otra cinco, es decir, el resultado no es el mismo.
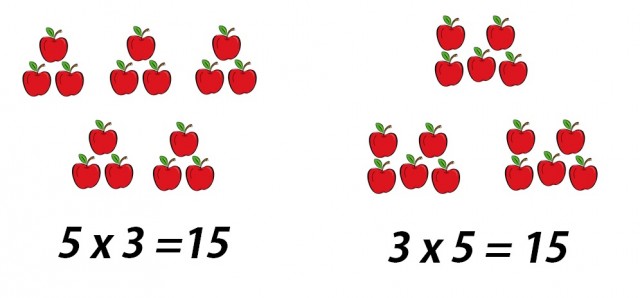
La clave, en definitiva, está en la palabra veces y no en la expresión ‘por’ que utilizamos en España. De esta forma, cinco veces tres da como resultado quince pero se entiende claramente la representación icónica. En el caso del cinco por tres, queda más dudoso.
Ahora bien, fuera del ámbito científico, en el día a día, la propiedad conmutativa se cumple en unas muy pocas ocasiones, la mayor parte del tiempo el orden de los factores sí altera el producto: no es lo mismo, estudiar y hacer un examen que hacer un examen y luego estudiar ¿a qué no?, tampoco se obtiene el mismo resultado si encendemos el calentador y nos damos una ducha que si nos damos una dicha y luego encendemos el calentador.
Y yendo un paso más allá: si salimos de casa una mañana, pasamos a recoger a nuestra mejor amiga, vamos juntas al gimnasio (después de cinco meses sin pisarlo) y le entrenadora nos preparar una sesión demoledora; de nada servirá repetir las series en orden inverso, salir del gimnasio, dejar a tu amiga en su casa y llegar a la tuya, que las agujetas del día siguiente las vas a tener. La propiedad conmutativa ni permite volver al pasado, ni arreglar lo que se rompe.
Sobre la autora: Maria José Moreno (@mariajo_moreno) es periodista
Alejandro Leon Maldonado
Es un craso error dar contra ejemplos de la propiedad conmutativa fuera del dominio de la matemática, que es donde tiene sentido. Refiero a los triviales ejemplos del estudio para el examen y de la visita al gimnasio con una amiga. Saludos.
Alejandro León
Investigador en Ciencia del Comportamiento
Universidad Veracruzana, México
Marco Antonio Raskolnikov
La propiedad conmutativa, jamás se dijo que aplica a todas las cosas de la vida, solo a la suma y la multiplicación. Creo que la autora se sale del tema
Javo
Totalmente de acuerdo, en el examen del chico no se está comprobando la conmutatividad que demuestra que el orden no altera el RESULTADO. Se está pidiendo la máxima representatividad de un producto usando la adición de sus elementos.
Komzt
Ud. comprobó de varias manera que la propiedad conmutativa existe en la matemática, no en otros contextos.
Elias
Las matemáticas se usan para entender la naturaleza, de hecho ahí nacen, entonces es una propiedad que en la física cuando quieras teorizar sobre algun fenomeno no sera muy utilizada, a eso va esa parte de la nota. Claramente es algo obvio pero hace entender el uso de las matemáticas.
Carlos e suarez
Que comentario tan ridiculo!!!!estamos hablando de matematicas!! Factores!!
Carlo Montagne
Para todos, la lectura matemática es única y de orden semántico codificado lógico, por tal motivo escribir 5×3 es lo mismo a decir 5 veces 3. Entonces el análisis justificador del examen de aquel desafortunado niño es erróneo (5+5+5), siendo la respuesta correcta 3+3+3+3+3.
Carlo Montagne
Es un hecho prospectivo que la conmutación es una ilusión justificada únicamente en el resultado y no en el proceso.
Director de Investigación
Instituto Tecnológico y Cooperación
LAC INTEC
MaGaO
¿Ein?
La propiedad conmutativa no es una ilusión, es una característica de ciertos procesos.
danirl barajas
En el ejemplo de las manzanas .. En efecto es el mismo resultado.. lo q cambia es el procedimiento de como llegar a ese resultado… Pero el resultado. En efecto es el mismo sin importar el procedimiento.. En mi opinion esta mal escrito ese articulo..
Alberto
No, no. El artículo confunde las cosas. El AXIOMA de CONMUTATIVIDAD dice: Sean a y b números reales. Entonces ab=ba para todo a y b en los reales. Jamás dice que a ó b representen manzanas. Cuando se modela algo matemáticamente, se debe ver que el modelo esté correcto. Al momento de hacer 3(5)=15 se está obteniendo el total de manzanas. De no ser así, no hay razón para efectuar el producto. Luego 5(3)=15 y por eso se sigue valiendo el axioma. El problema está en hacer igualdad entre montones, esos no son números. Sólo la cantidad(número) que representan, pueden ser iguales, no los conjuntos. Otro detalle es que confunde lógica proposicional con lógica temporal. En lógica proposicional, dadas p y q proposiciones, siempre (p^q) es lógicamente equivalente a (q^p), i.e., (p^q)=(q^p) donde ^ es la conjunción. En lógica temporal, eso no es cierto siempre y esos son los ejemplos que ponen en el artículo, son de lógica temporal, no proposicional. Tener cuidado, no confundir operaciones entre números, que operaciones con conjuntos.
W.Laínez
La propiedad conmutativa esta muy clara: el orden de los componentes no alteratá el resultado (solo en suma y multiplicación) y en el caso de las manzanas la ley se cumple el resultado es el mismo … Que los componentes utilizados estan ordenados de diferente forma es otro tema además la P. Conmutativa es específica no cambiará el resultado no dice que no cambiará el agrupamiemto de los componentes y todo esto aplicado a la lógica matemática …Universidad Autónoma De Santa Ana , El Salvador …
Enrique Romeo
Totalmente fuera de lugar sus conclusiones.
gabriela
Me parecen pésimos sus «ejemplos» de una falsa conmutatividad, porque sólo aplica a la suma y a la multiplicación.
La razón de por qué el profesor puso como malas las respuestas del alumno, es porque no interpretó lo que estaba escrito, y eso era seguramente el tema tratado en la clase, porque se ve lo mismo en la pregunta 4 x 6 , en que el alumno dibuja seis veces cuatro.
Salvador
A la autora María José Moreno: La propiedad conmutativa aplicada a las operaciones aritméticas de adición y multiplicación, no aplican necesariamente en circunstancias cotidianas fuera del contexto matemático, como bien apuntan Alejandro León, Marco Antonio Raskolnikov y Gabriela. Consideró que no aportas gran cosa en el entendimiento de porqué se califica como mal la respuesta y si contribuyes a confundir la gimnasia con la magnesia en tus ejemplos. A mi parecer, en el primer reactivo ¿no se aplicó la estrategia de sumas repetidas? En el segundo ¿si giras la hoja 90 grados no se ve escrito el otro arreglo de 4×6?¿acaso se debe adoctrinar a resolver los problemas de una única forma en lugar de educar para pensar de distintas maneras? Si estoy mal corrijanme. Aceptó críticas.
Daniel
No entiendo esta entrada…
César Tomé
Es muy simple. Tiene dos partes:
a) En la primera se trata la anécdota del examen y cómo es fácilmente entendible la corrección del profesor con solo cambiar el idioma en el que se piensa.
b) La segunda «fuera del ámbito científico», con ejemplos de la mala aplicación de la propiedad conmutativa a la vida cotidiana, es humorística.
Esta entrada no es ni pretende ser un tratado matemático. La sección «Frontera» del Cuaderno se llama así porque trata asuntos que están en el límite de la ciencia con la vida del común de los mortales.
No hay que buscarle tres pies al gato.
Momentum
A menos que sea posible viajar en el tiempo.. y ya estamos camino a lograrlo, o quizas ya lo logramos.. si tenes en cuenta el universo entero Cómo Una entidad única, como una sabana hecha de espacio tiempo, no hay una dirección específica en la que avanza, el universo simplemente existe, se puede ir en todas direcciones
Bryan Maroto
El error de la escritora radica en que confunde una propiedad derivada de una ley física (la entropía) con una propiedad lógica (conmutatividad) que tiene aplicaciones matemáticas y no físicas.
Josué
La propiedad conmutativa de la multiplicación tiene muchísimas aplicaciones donde sin ella no sería posible construir un conocimiento significativo de la ciencia de los números. El uso de los contraejemplos de la vida real demuestra una corriente que, a la vez de pretender trivilizar la matemática en su forma pragmática, hace ver el escaso conocimiento que se tiene de ella. Yo, en lo personal, no puedo ponerme a criticar algo que no conozco a profundidad ¡Es una lástima que los demás no lo vean así!
Hitos en la red #112 – Naukas
[…] de comentarios de aquellos que no se han parado a leer el artículo dos veces antes de comentar), Las mentiras de la propiedad conmutativa de Mariajo Moreno; a matemáticas con todos los perejiles, Euler y el último teorema de Fermat de […]
Pablo Rodríguez Sánchez
Nunca dejará de fascinarme la polémica que levantan los artículos que tocan temas matemáticos básicos. ¡Son aún más delicados que los de política!
Mariajo Moreno
Buenos días
Gracias a todos por sus comentarios, siento no haber podido responder antes por lo que agradezco que Cesar Tomé lo haya hecho por mi.
Saludos
Science and Space For Knowledge
Es bueno acercar el mundo matematico a la realidad cotidiana, pero por favor no con ejemplos que «salen de contexto» como los citados en el articulo.
Un buen ejemplo basico y de moda porque es «ambiental» y que de hecho daria razon a la respuesta del ninnio : Si el chico va al supermercado a comprar manzanas (15 que le han encargado en casa), para él es mas sencillo tomar tres bolsas y poner 5 manzanas en cada una; que tomar 5 bolsas y poner 3 manzanas en cada una !!! y de hecho proteger el planeta ! que es lo mas importante. Esto si seria un buen ejemplo, solo que da la razon al estudiante y no al profesor.
Los buenos educadores, y lo digo porque he tenido excelentes profesores en mi vida, son aquellos que descubren los talentos de cada estudiante y los explotan al maximo ! para crear pensadores, cientificos y personas capaces de enfrentar y solucionar problemas matematicos o de la vida cotidiana, gracias a la buena educacion recibida.
Si bien se trata de matematica, es tambien importante ensenar a los alumnos que siempre hay diferentes maneras de obtener un resultado correcto.
Cordialmente, Luz
Victor Monsalve
Buenas tardes.
Concuerdo con lo que mencionan algunos cometarios. Creo que no es apropiado comparar situaciones cotidianas con una propiedad que se aplica en el ámbito matemático.
Creo que, en este sentido más que poner atención al error planteado, hay que enfocarse en de qué manera se ha planteado (y se plantea) este concepto a los estudiantes. Pienso que es importante tener claridad del concepto, para no generar confusiones en los estudiantes, a futuro.
Éxito a todos!!!