Quiero ir de Bilbao a Pamplona en coche, así que abro Google Maps para recordar cuántos kilómetros debo recorrer…

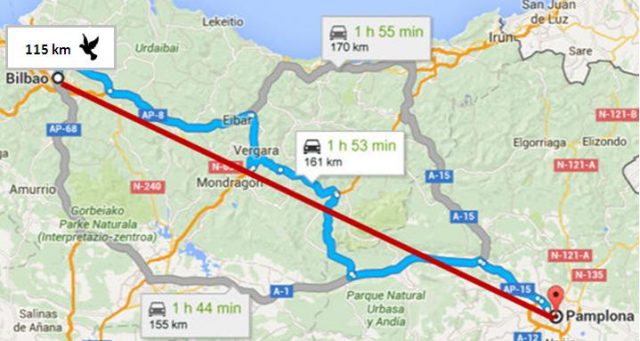
¡Vaya! El servidor ofrece tres rutas alternativas por carretera, una de 155 km, otra de 161 km y la última de 170 km. Además, ‘a vuelo de pájaro’ –en línea recta sobre el mapa–, la distancia es de 115 km. Entonces, ¿cuál es realmente la distancia entre Bilbao y Pamplona?

Las cuatro: en cada caso, lo que estamos haciendo es elegir el ‘camino más corto’ entre Bilbao y Pamplona, cuando exigimos ir por una carretera concreta.

En matemáticas, una distancia –o métrica– es una función que asigna a cada par de puntos a y b en un conjunto un número no negativo cumpliendo ciertas propiedades adicionales bastante razonables e intuitivas: la distancia entre a y b es nula si y sólo si los puntos son iguales, cumple la propiedad simétrica (la distancia entre a y b es la misma que entre b y a) y verifica la desigualdad triangular (si tenemos tres puntos, a, b y c, la distancia entre a y c es menor o igual que la suma de las distancias entre a y b y entre b y c).

¿Cuál es la distancia más corta entre dos puntos? Depende; hay muchas maneras de definir métricas sobre un conjunto (ver, por ejemplo [1]). En el caso presentado al principio, la elección de la carretera entre Bilbao y Pamplona puede reducir o aumentar el kilometraje; aunque siempre hemos oído que ‘la línea recta es la distancia más corta’, esta afirmación es matizable, dependiendo de la situación en la que nos encontremos. Veamos otro ejemplo para entender mejor esta afirmación.

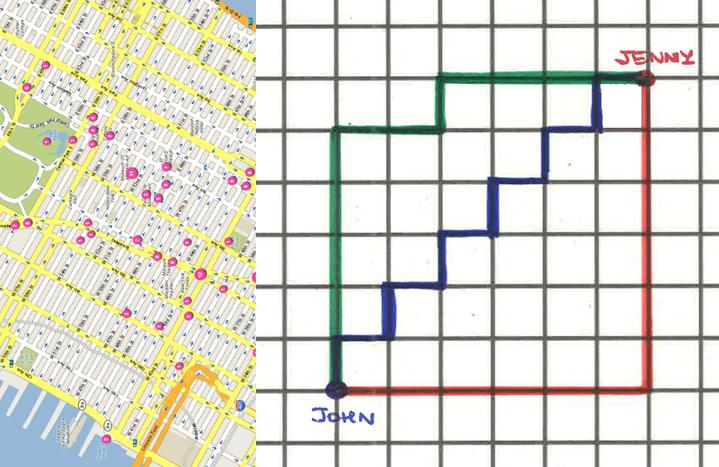
Imaginemos una ciudad como Manhattan, en la que las calles se cortan en ángulo recto formando una cuadrícula perfecta. John quiere a ir a visitar a Jenny que vive 6 calles al norte y 6 al este respecto a su casa; como no tiene dinero, John debe realizar el trayecto a pie. ¿Cuál es el camino más corto para llegar a casa de su amiga? Suponiendo que todas las cuadrículas miden lo mismo, los tres trayectos marcados en la imagen 2 son igual de cortos –y son, de hecho, los más cortos–. La longitud del trayecto marcado en rojo es lo que en matemáticas se llama la distancia de Manhattan entre los puntos que representan las casas de John y de Jenny.

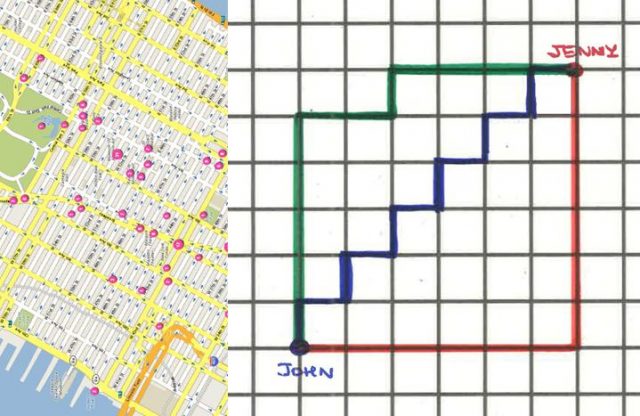
Si lo pensamos en coordenadas, y los dos puntos son a=(a₁,a₂) y b=(b₁,b₂), la distancia de Manhattan entre a=(a₁,a₂) y b=(b₁,b₂) es |a₁-b₁|+|a₂-b₂|.

En este caso, la distancia de Manhattan entre las casas de John y Jenny es de 12 unidades; es el camino más corto entre esos dos puntos, aunque ese recorrido mínimo puede realizarse por caminos alternativos –por ejemplo, el verde o el azul en la imagen 2–. Si medimos la distancia en línea recta –la distancia usual entre dos puntos– entre las casas de los dos amigos, el teorema de Pitágoras dice que es de 6 ~ 8,48… y este número es menor que 12. En efecto, lo es, pero John no puede realizar a pie ese recorrido ideal…

Referencias

[1] Juan Monterde, Espacios métricos y geometría Riemanniana, Un paseo por la geometría 2000/2001, 1-24, 2001.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.