El pasado 1 de junio, César Tomé me hizo una llamada en twitter en el enlace que había puesto del artículo Simple Set Game Proof Stuns Mathematicians, publicado en QUANTA Magazine. Un excelente artículo en el que se explicaba la demostración, cuya simplicidad –en relación a otros problemas matemáticos similares- había sorprendido a la comunidad matemática, de un problema de combinatoria relacionado con el juego de cartas SET. En la entrada de hoy, y en la siguiente, vamos a hablar de este juego y de algunas de las matemáticas relacionadas con el mismo.

El juego de cartas SET es uno de esos juegos llamados “de percepción visual” y que mi amigo Iñaki, de la Juguetería Pinocchio de Bilbao, me había recomendado en más de una ocasión, ya que teniendo en cuenta su experiencia vendiendo juegos (muchos de ellos de ingenio), consideraba que este era muy interesante y divertido, y que enganchaba a las personas en cuanto empezaban a jugar al mismo.

Pero vayamos con la descripción y las reglas del mismo. SET es un juego formado por una serie de cartas, cada una de las cuales consta de un diseño sobre fondo blanco. Este diseño está determinado por cuatro características:

1) la forma de los símbolos (óvalos, ondas o rombos);

2) los colores (rojo, verde o morado);

3) el número de símbolos (uno, dos o tres);

4) el fondo del símbolo (sólido, rayado o hueco).

Y puesto que las cartas combinan todas estas características del diseño de forma exhaustiva, existen exactamente 3⁴ = 81 cartas diferentes en el mazo del SET.

Como el objetivo del juego es conseguir formar un SET de entre las 12 cartas que deben de estar boca arriba sobre la mesa, expliquemos qué es exactamente un SET.

SET: tres cartas forman un SET si, respecto a cada una de las cuatro características (forma, color, número y fondo), evaluadas una a una, las tres cartas son iguales o las tres son diferentes.

Por ejemplo, las tres cartas de la imagen anterior forman un SET, puesto que las tres tienen diferente forma, diferente color, diferente número y diferente fondo.

De igual forma, los dos grupos de tres cartas siguientes son ejemplos de SETs. En el primero, las tres cartas tienen diferentes formas y colores, mientras que tienen el mismo número de símbolos, tres, y el mismo fondo, sólido; y en el segundo grupo, las tres cartas tienen la misma forma, ondas, y el mismo color, morado, pero distinto número y fondo.

Por el contrario, los dos siguientes no forman un SET. En el primero, aunque las tres cartas tienen el mismo número y forma, y todas tienen distinto color, sin embargo, el fondo es igual en dos de ellas, sólido, y diferente en la tercera, rayado. Y algo similar ocurre en el siguiente grupo, donde la condición para formar un SET se rompe en relación a la forma.

Dadas dos cartas cualesquiera, existe exactamente una carta que junto a las dos anteriores forma un SET. Esto se debe a que existen todas las combinaciones posibles de las cuatro características, luego dadas dos cartas cualesquiera, lo que ocurre con cada una de las cuatro características para ellas dos determina como será la característica de la tercera (por ejemplo, si esas dos cartas tienen el mismo color, la tercera también lo tendrá, pero si esas dos cartas tienen dos fondos distintos, la tercera carta tendrá el fondo que falta), y por lo tanto, qué carta es.

Además, nos podemos plantear cuántos SETs distintos se pueden realizar con las 81 cartas que conforman el juego. Como cada dos cartas determinan un SET, parecería que la respuesta es el número de formas de elegir dos cartas de entre las 81, pero como así estamos contando cada SET concreto tres veces, hay que dividir entre 3, luego existen…

SETs distintos.

Completemos ahora las reglas del juego SET, al que pueden jugar un solo jugador, en modo solitario, o varios jugadores, y que en las instrucciones que la empresa Devir incluye con el juego, se recomienda este a partir de los 6 años.

Una de las personas que juega debe hacer el papel de repartidora de cartas en el juego. Empezará colocando 12 cartas boca arriba en la mesa a la vista de todos los jugadores, formando un rectángulo 4 x 3. En este juego no existen turnos, tras colocarse las 12 cartas todos los jugadores buscan un SET y el primero en localizarlo debe gritar “SET”, momento en el que se interrumpe el juego. Se comprueba que efectivamente es un SET, en cuyo caso dicho jugador se guarda las tres cartas, se colocan otras tres cartas del mazo en su lugar, completando las 12 sobre la mesa, y se continúa el juego. Si el SET no fuese correcto, el jugador devolverá las tres cartas a su sitio, y perderá tres de sus cartas ganadas anteriormente.

Si en algún momento de la partida todos los jugadores coinciden en que es imposible realizar un SET, se añaden 3 cartas más, teniendo 15 sobre la mesa, y en el momento que se retiren tres cartas por un nuevo SET no se reemplazarán para que vuelva a haber 12 sobre la mesa. Si con 15 cartas no se pudiese tampoco formar un SET se volverían a añadir tres cartas más, así hasta que sea posible realizar uno. El juego continúa hasta que se acaban las cartas del mazo y gana el jugador que ha conseguido más cartas.

Pero lo mejor para entender la dinámica de este juego es simplemente jugar. En la siguiente imagen se muestra un grupo de 12 cartas sobre la mesa, con las que se pueden formar 6 SETs distintos.

Existen varias páginas web para jugar al SET solitario online. Una es la página de crucigramas del New York Times y otra es setgame.mooo.com.

El juego de cartas SET fue diseñado por la genetista Marsha J. Falco en 1974 y comercializado en 1991 a través de la empresa SET Enterprises. Como se explica en la página web de la empresa SET Enterprises, Marsha J. Falco estaba tratando de entender si la epilepsia en los perros pastores alemanes era hereditaria. Para estudiar los genes y cromosomas de las células de los perros, la genetista creó unas cartas en las que incluía la información de cada perro. Como ciertos bloques de información eran los mismos en cada carta utilizó símbolos para representar bloques de información, en lugar de escribir explícitamente toda esa información. Utilizó símbolos con diferentes características para representar diferentes combinaciones de genes. Mientras estaba explicando las combinaciones a los veterinarios con los que trabajaba, se dio cuenta de lo divertido de las combinaciones de los diferentes símbolos, y nació así el juego de cartas SET.

Pero volviendo a las reglas del juego, hemos comentado que si en algún momento de la partida no se puede conformar ningún SET con las 12 cartas que hay sobre la mesa, se añadirán 3 cartas más y así hasta que se pueda formar un SET. Nos podemos plantear por tanto dos cuestiones:

Cuestión 1: ¿Cómo de probable es que no se pueda formar un SET con las 12 cartas que hay sobre la mesa?

Teniendo en cuenta que hay combinaciones distintas de 12 cartas que pueden ponerse sobre la mesa, habría que ver cuántas de ellas no dan lugar a ningún SET.

Cuestión 2: ¿Cuál es el número mínimo de cartas que debe de haber sobre la mesa para poder asegurar que siempre es posible formar un SET?, o equivalentemente, ¿cuál es el número máximo de cartas que puede haber sobre la mesa de forma que no se pueda realizar un SET?

Responder a estas cuestiones, y otras similares, en la era de los ordenadores, es relativamente sencillo. En la página web Mathematics Stack Exchange se explica que el experto en programación Donald Knuth, autor del libro The Art of Computer Programming, escribió algunos programas informáticos en 2001 (que se pueden encontrar en su página web) para calcular las cantidades relacionadas con estas cuestiones. Y en general la cuestión siguiente. Si consideramos que haya m cartas sobre la mesa (12 en el caso del juego y la cuestión 2), cuántas de las combinaciones de m cartas que se pueden dar con las 81 cartas del juego no producen ningún SET, o de una forma probabilística…

Cuestión 3: ¿Cuál es la probabilidad de que con m cartas sobre la mesa no exista (o respectivamente, exista) un SET?

En la página web Mathematics Stack Exchange se han calculado de nuevo estos datos, el número de las combinaciones de m cartas que no producen ningún SET y la probabilidad de que esto ocurra, respondiendo así a la cuestión 3, y las anteriores. A continuación, mostramos la tabla de probabilidades de que SÍ exista un SET con m cartas sobre la mesa (para m tomando valores desde 1 hasta 21):

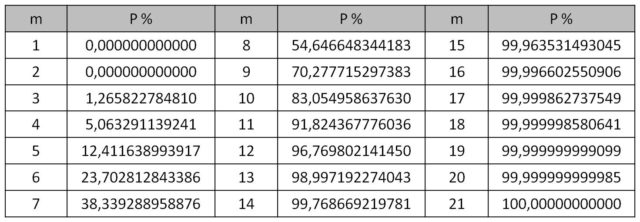
A partir de la tabla anterior, podemos sacar algunas conclusiones.

– Conclusión 1:La probabilidad de que sacando tres cartas al azar del mazo de 81 cartas se obtenga un SET (m = 3) se calcula fácilmente (no hace falta un ordenador), puesto que es el número de SETs posibles (1.080, como hemos calculado anteriormente) dividido por el número total de grupos de tres cartas . Pero también, como dadas dos cartas cualesquiera existe exactamente una, de entre las 79 restantes, con la que formar un SET, esa probabilidad es efectivamente 1/79.

– Conclusión 2: La probabilidad de que exista un SET dadas 12 cartas cualesquiera sobre la mesa (Cuestión 1, m = 12) es del 96,77%, luego es poco probable que no se encuentre un SET (el 3,23%) y que haya que añadir 3 cartas más.

– Conclusión 3: La probabilidad de hacer un SET si consideramos 15 cartas sobre la mesa es, como se ve en la tabla, del 99,96%, y en consecuencia, la probabilidad de que no se pueda conseguir es del 0,04% (1 de cada 2.700). Sin embargo, en el juego no tenemos 15 cartas aleatorias, sino que partimos de 12 cartas en las que sabemos que no es posible encontrar un SET, y les añadimos 3 más, entonces la probabilidad de no poder hacer un SET con esas 15 cartas es más alta, del 1,14% (1 de cada 88).

– Conclusión 4: El número máximo de cartas que puede haber sobre la mesa de forma que no se pueda realizar un SET (Cuestión 2) es 20, a partir de esa cantidad siempre se puede realizar un SET.

Todo esto respecto a si existe, o no, un SET cuando tenemos 12 cartas sobre la mesa, o incluso otro número de cartas, pero otra cuestión interesante que nos podemos plantear es cuál es la media de SETs que pueden realizarse en un grupo de 12 cartas. Si lo pensamos un poco, el número de SETs que se pueden obtener, de media, en un conjunto de 12 cartas es

Pero volviendo a la cuestión 2 (¿cuál es el número máximo de cartas que puede haber sobre la mesa de forma que no se pueda realizar un SET?), es curioso que la respuesta, es decir, que el número es 20, fue obtenida realmente por el matemático italiano Giuseppe Pellegrino en 1971, tres años antes de que se inventara el juego SET. Esto se debe a que cuando se interpreta el juego SET y la cuestión 2 anterior utilizando un modelo geométrico, de rectas sobre un espacio de dimensión 4, lo cual es el objetivo de mi siguiente entrada de la sección Matemoción del Cuaderno de Cultura Científica, se descubre que la respuesta ya la había dado Pellegrino en 1971.

Para terminar por hoy, volvamos al problema matemático que se acaba de resolver por parte de la comunidad matemática, y que aparece en el artículo de la revista QUANTA Magazine anteriormente citado, que no es más que es una generalización de la cuestión 2 anterior. Expliquémoslo.

Desde las matemáticas se plantearon el considerar más características en los diseños de las cartas del juego SET, además de las cuatro dadas. Por ejemplo, una nueva característica, si realmente quisiéramos construir tal juego y que no fuese solo un ejercicio intelectual, podría ser que los bordes de los dibujos fueran lisos, con rayas o con semicircunferencias.

En consecuencia, desde las matemáticas se pensó en un juego de cartas SET generalizado, en el cual los diseños de las cartas vinieran determinados por n características distintas, y que cada característica, como en el juego original, tuviese 3 opciones (donde el número de características podía ir desde la simplicidad de una única característica, n = 1, pasando por el juego original de n = 4 características, o cualquier otra cantidad n de características). En consecuencia, el número de cartas que formarían el juego SET generalizado sería de 3ⁿ.

En estas condiciones, se plantearon el problema combinatorio que generalizaba la cuestión 2 anterior, y cuya resolución ha tenido ocupada a parte de la comunidad matemática estos años.

Problema: ¿Cuál es el mayor número de cartas que se pueden poner sobre la mesa, en el juego SET generalizado de n características, de forma que no se pueda formar un SET?

En mi siguiente entrada de la sección Matemoción veremos cómo trasladar el juego SET a un modelo geométrico, y los primeros pasos en la resolución del problema anterior.

Bibliografía

1.- Erica Klarreich, Simple Set Game Proof Stuns Mathematicians, QUANTA magazine, 31/05/2016

2.- Página web del juego SET en la empresa que lo ha comercializado en España, DEVIR

3.- Página web de la empresa SET Enterprises

4.- Página web Mathematics Stack Exchange

5.- Página web de Donald Knuth

6.- Benjamin Lent Davis y Diane MacLagan, The Card Game Set, The Mathematical Intelligencer 25, n. 3, p. 33-40, 2003.

7.- Giuseppe Pellegrino, Sul massimo ordine delle calotte in S_4,3, Matematiche (Catania), 25, p. 149-157 (1971), 1970.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica