En mi anterior entrada del Cuaderno de Cultura Científica, titulada Matemáticas en el juego de cartas SET (1), me hacía eco de la noticia de la resolución de un problema matemático relacionado con el juego de cartas SET, y aprovechaba para explicar el juego y algunos aspectos combinatorios y probabilísticos del mismo.

En esta segunda entrada, vamos a introducirnos en el modelo geométrico que se ha utilizado para estudiar el problema, así como en algunas de las técnicas geométricas y combinatorias utilizadas para demostrar resultados iniciales del mismo.

Recordemos que el juego está formado por 81 cartas, cada una de las cuales consta de un diseño determinado por cuatro características: 1) la forma de los símbolos (óvalos, ondas o rombos); 2) los colores (rojo, verde o morado); 3) el número de símbolos (uno, dos o tres); 4) el fondo del símbolo (sólido, rayado o hueco).

El objetivo del juego, ya se juegue en modo solitario o entre varias personas, es formar un SET con las 12 cartas colocadas previamente boca arriba encima de la mesa de juego. Además, tres cartas forman un SET si, respecto a cada una de las cuatro características (forma, color, número y fondo), evaluadas una a una, las tres cartas son iguales o las tres son diferentes. En la imagen anterior vemos dos ejemplos de tríos de cartas formando un SET, las tres cartas de la caja, que forman un SET porque tienen las tres formas distintas, los tres colores distintos, el mismo número de símbolos, dos, y el mismo fondo, sólido, mientras que las otras tres cartas forman un SET porque tienen diferentes las cuatro características.

Cada vez que se completa un SET el jugador que lo consigue retira las tres cartas y las sustituye por otras tres del mazo de cartas sin jugar aún. Si no se pudiese formar ningún SET entre las 12 cartas, se añadirían 3 cartas más. Aunque es bastante improbable (véase la anterior entrada) podría no poder formarse tampoco un SET con esas 15 cartas. La cuestión que atrajo la atención de la comunidad matemática fue conocer cuál es el mayor número de cartas con las que no se puede realizar un SET. Como se comentó en la anterior entrada, la respuesta es 20.

Siguiendo una de las técnicas habituales de trabajo dentro de las matemáticas, se consideró la siguiente generalización del problema. Pensemos en un juego de cartas SET generalizado, en el cual los diseños de las cartas vinieran determinados por n características distintas (en el original, n = 4, forma, color, número y fondo), y que cada característica, como en el juego original, tuviese 3 opciones (por lo tanto, el número de cartas del juego generalizado es ), el problema combinatorio generalizado que se abrió ante los matemáticos fue el siguiente.

Problema: ¿Cuál es el mayor número de cartas que se pueden poner sobre la mesa, en el juego SET generalizado de n características, de forma que no se pueda formar un SET?

El objetivo de esta entrada es describir el modelo geométrico que se utilizó desde las matemáticas para describir el juego SET generalizado y el problema combinatorio abierto, así como las técnicas que empezaron a utilizarse en la resolución del mismo.

Para simplificar, vamos a describir primero el modelo geométrico para el juego SET original de 4 características. Para empezar, y teniendo en cuenta que hay solo 3 valores para cada una de las características, se consideran los “enteros módulo 3”, es decir, se reduce el conjunto de todos los números enteros y su aritmética al conjunto finito {0, 1, 2}, a partir del número 2, los demás enteros se identifican de forma cíclica con los del conjunto {0, 1, 2}, así 3 = 0, 4 = 1, 5 = 2, 6 = 3, etcétera, de forma similar a las horas de un reloj que serían como los enteros módulo 12 (las 13 horas es la 1, las 14, son las 2, etcétera). Los enteros módulo 3, que se denotan , tienen la estructura algebraica de cuerpo, con las operaciones suma y multiplicación naturales restringidas al mismo (, , , , , , , para cualquier ).

En estas condiciones, se identifican las cartas del juego SET con los puntos del espacio geométrico de dimensión 4 , formado por todas las 4-tuplas de números de , es decir, , para . Cada una de las cuatro entradas de la 4-tupla refleja una de las cuatro características descritas arriba (forma, color, número y fondo), y se asigna el número 1, 2 o 0 (recordemos que 3 = 0) en función de que valor tome de los tres posibles.

Por ejemplo, la primera carta del SET de la imagen siguiente se correspondería con el punto (2, 1, 0, 1) puesto que la forma es la onda (2), el color rojo (1), el número 3 (0) y el fondo sólido (1). Mientras que las otras dos con los puntos (0, 2, 2, 1) y (1, 0, 1, 1).

Una vez establecido el espacio geométrico básico que describe el conjunto de las cartas del juego, veamos cuál es el significado geométrico de la propiedad de formar un SET. Tres cartas forman un SET si, respecto a cada una de las cuatro características, evaluadas una a una, las tres cartas son iguales o las tres son diferentes, luego dados tres puntos de , las cartas que representan forman un SET si al fijarnos en las coordenadas de los puntos, una a una, las tres son distintas (luego, 1, 2, 0) o las tres son iguales. Por lo tanto, si tenemos en cuenta que las coordenadas pertenecen a , podemos concluir lo siguiente.

Dados tres puntos en , forman un SET si, y sólo si, .

Así ocurre, por ejemplo, con los tres puntos del SET de la imagen anterior.

Y teniendo en cuenta que en el espacio geométrico (espacio vectorial) , la propiedad es equivalente a que los puntos A, B y C están en la misma recta, puesto que , entonces tenemos la siguiente condición geométrica del SET.

Propiedad geométrica SET: Tres puntos latex Z^4_3$ representan cartas que forman un SET si, y sólo si, los puntos A, B y C están sobre una misma recta en el espacio geométrico .

Esta construcción es también válida para el juego SET generalizado de n características. Cada carta del SET generalizado se identifica con un punto del espacio geométrico de dimensión n, , formado por las n-tuplas de números de , y tres puntos forman un SET si están en la misma recta.

En estas condiciones, considerado el modelo geométrico, se define un n-cap como un subconjunto de que no contiene ninguna recta completa (tres puntos), que es el concepto geométrico que nos describe un conjunto de cartas que no admiten un SET. Por lo tanto, el problema planteado anterior se transforma en el modelo geométrico en el siguiente.

Problema geométrico: ¿Cuál es el tamaño (es decir, número de puntos) más grande que puede tener un n-cap en ?

A un n-cap de tamaño máximo se le llama n-cap máximal, y podemos denotar su tamaño, el número de puntos del mismo, como a_n.

En la anterior entrada sobre el juego de cartas SET comentamos que el número máximo de cartas que puede haber sobre la mesa de forma que no se pueda realizar un SET es 20, es decir, el tamaño de un 4-cap maximal, de un subconjunto de puntos en que no contiene rectas. Más aún, en dicha entrada habíamos mostrado un ejemplo de 20 cartas sobre las que no se podía realizar un SET, es decir, consideradas estas como puntos del espacio geométrico , dan lugar a un 4-cap maximal.

La respuesta al problema fue obtenida por el matemático italiano Giuseppe Pellegrino en 1971, tres años antes de que se inventara el juego SET, debido a que Pellegrino realmente contestó a la cuestión matemática anterior sobre la existencia de 4-cap maximales.

Con la ayuda de los ordenadores, y muchas matemáticas, se fueron calculando poco a poco algunos de los tamaños de unos pocos n-caps maximales, aunque sólo para dimensiones bajas. De hecho, para dimensión 5 se demostró en el año 2002 [5] y para dimensión 6 en 2008 [6].

Además de estos resultados, sólo se habían conseguido obtener algunas cotas al tamaño de los n-caps maximales. Por ejemplo, que los tamaños de estos eran más pequeños que 1/n veces el tamaño del mazo de cartas del juego, que es [8]. Hace unas semanas, en el artículo Simple Set Game Proof Stuns Mathematicians, publicado en QUANTA Magazine, se anunciaba la resolución del problema geométrico anterior, asociado al juego de SET generalizado, que a pesar de la dificultad inicial del problema, su demostración ha resultado ser más sencilla (dentro del contexto de la investigación matemática actual) de lo esperado.

En la parte final de esta entrada, vamos a demostrar que a₂ = 4, es decir, 4 es el tamaño de un 2-cap maximal, o lo que es lo mismo, en un juego de SET generalizado de solamente dos características el número máximo de cartas sobre la mesa (de las 9 cartas que tiene el mazo en este caso) sobre las que no se puede hacer un SET es 4. El juego SET de dos características es extremadamente sencillo y el problema asociado trivial, sin embargo, su análisis nos va a permitir revisar y entender mejor el modelo geométrico anteriormente descrito, y además, realizaremos una sencilla demostración combinatoria para ilustrar algunas de las técnicas utilizadas en este problema.

Para el juego SET generalizado de sólo dos características vamos a considerar las dos características primeras del juego original, forma y color.

El espacio geométrico asociado al juego SET de dos características es el plano , es decir, el plano formado por todas las 2-tupas , con . Si pensamos en el plano euclidiano clásico, formado por todas los pares , con números reales cualesquiera, este es el plano “usual”, formado por los infinitos puntos dados por esas dos coordenadas. Sin embargo, nuestro plano está formado únicamente por 9 puntos distribuidos “en el plano usual” formando una especie de cuadrado (véase la siguiente imagen) y además es cíclico, es decir, al llegar al extremo derecho se continúa por el izquierdo y al llegar a la parte superior se continúa por abajo, ya que los números son enteros módulo 3, de .

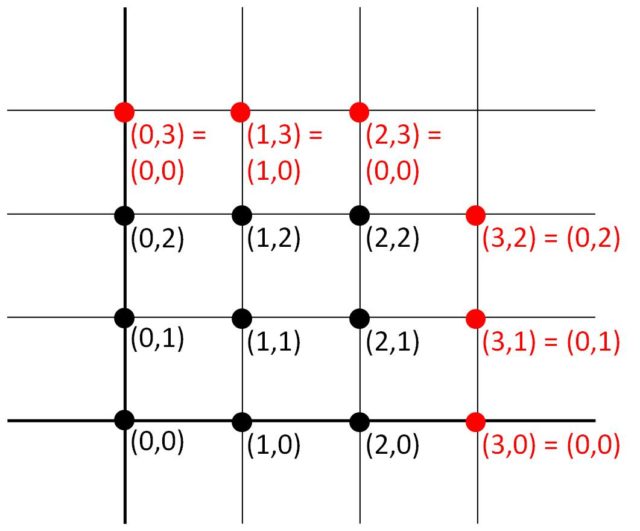
Observemos que los diferentes puntos (en negro) del plano de la imagen de arriba, se corresponden (siguiendo el orden de las imágenes) con las cartas del SET de la imagen anterior. El punto (0,0) es la carta con el rombo morado, el punto (1,0) el óvalo morado, etcétera.

Además, como hemos comentado anteriormente, cada grupo de tres cartas realizando un SET se corresponde con tres puntos que forman una recta completa de este plano. En la imagen siguiente tenemos dos ejemplos, la recta marrón (2,0)-(2,1)-(2,2) y la recta azul (0,1)-(1,2)-(2,0). Efectivamente, la suma de las coordenadas de los puntos es siempre cero, en la primera recta 2 + 2 + 2 = 6 = 0 y 0 + 1 + 2 = 3 = 0 (no olvidemos que las coordenadas son números de ), y lo mismo para la otra.

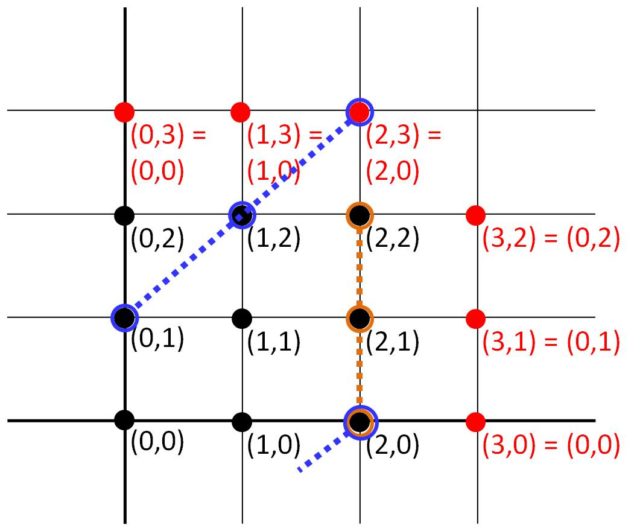, que se corresponden con dos grupos de cartas que forman SET" width="400" height="332" srcset="https://culturacientifica.com/app/uploads/2016/07/imagen-9-640x531.jpg 640w, https://culturacientifica.com/app/uploads/2016/07/imagen-9-193x160.jpg 193w, https://culturacientifica.com/app/uploads/2016/07/imagen-9-768x637.jpg 768w, https://culturacientifica.com/app/uploads/2016/07/imagen-9.jpg 1061w" sizes="(max-width: 400px) 100vw, 400px"> Dos rectas del plano discreto de 9 puntos , que se corresponden con dos grupos de cartas que forman SET

Ahora, nos planteamos el problema geométrico de buscar cuál es el tamaño de cualquier 2-cap maximal, es decir, el número de puntos de un subconjunto, de tamaño máximo, del plano de 9 puntos que no contiene ninguna recta completa (tres puntos). En este caso, es fácil construir un 2-cap con cuatro puntos, como el que se muestra en la imagen, y no es difícil ver que no se puede obtener uno de 5 puntos, luego el anterior es maximal.

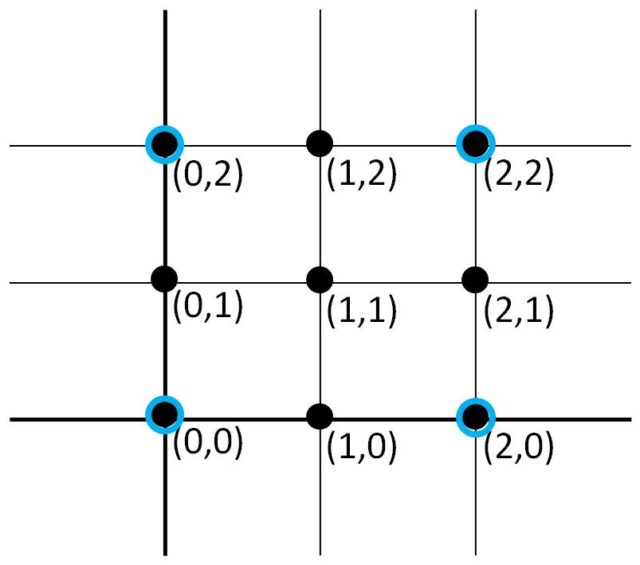
Más adelante realizaremos una demostración matemática, con técnicas de la Combinatoria, de este hecho, a₂ = 4, pero antes veamos algunos otros ejemplos de caps maximales en dimensiones bajas.

Si tenemos en cuenta que el espacio tridimensional , asociado al juego SET de tres características, es el espacio tridimensional de los puntos que se expresan como ternas , con , entonces estos 27 puntos representan un cubo tridimensional. Este lo podemos pensar como tres copias de nuestro plano de 9 puntos anterior al que le añadimos la tercera coordenada de los puntos, la cual indica la altura, nivel 0, 1 o 2.

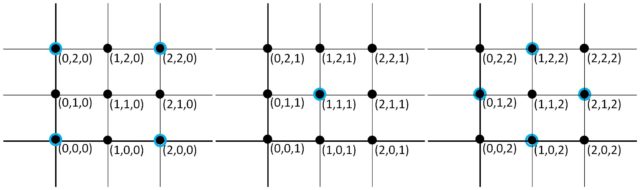
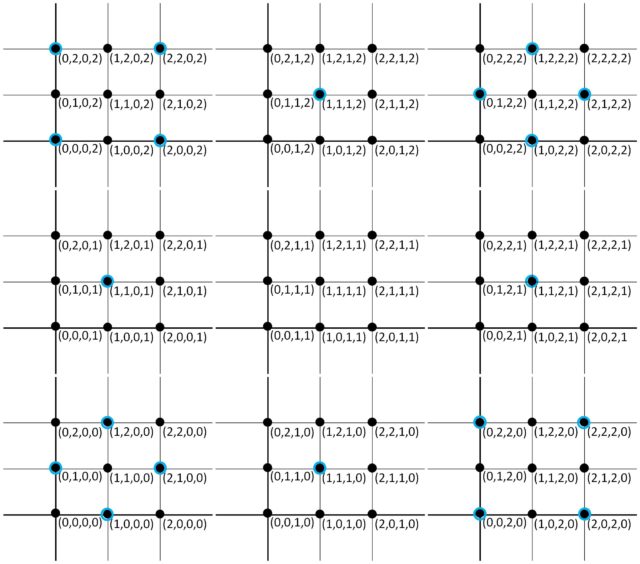
De forma análoga a lo anterior, los 81 puntos del espacio de dimensión cuatro formarían un hipercubo, que lo vamos a representar utilizando tres niveles para la nueva altura.

Para finalizar, como ya hemos anunciado, la demostración combinatoria de que un 2-cap maximal tiene 4 puntos.

Puesto que hemos mostrado un ejemplo de 2-cap con 4 puntos, basta con probar que no es posible un 2-cap con 5 puntos.

Supongamos que existiera un 2-cap con 5 puntos, que denotaremos A, B, C, D, E. Teniendo en cuenta que el plano de 9 puntos se puede descomponer como unión disjunta de tres rectas horizontales y el 2-cap no puede contener una recta, cada una de las tres rectas horizontales contiene como mucho dos de los puntos del 2-cap. Luego hay dos rectas horizontales con dos puntos y una con un único punto (como en el ejemplo de la imagen siguiente).

Sea A dicho punto (como en la imagen) y llamemos s a esa recta horizontal que contiene a A. Existen exactamente cuatro rectas del plano que contienen a A, la recta s y tres más, r₁, r₂ y r₃.

Como s no contiene a los puntos B, C, D y E, tenemos 4 puntos que están en tres rectas (r₁, r₂ y r₃), luego por el principio del palomar (véase la entrada Principio del palomar, una potente herramienta), existen dos puntos, de entre B, C, D, E, que están en una misma recta, pero como también está A en ella, entraríamos en contradicción con el hecho de que el conjunto A, B, C, D, E es un 2-cap y no contiene rectas completas (tres puntos). En conclusión, no existe un 2-cap con 5 puntos.

Un argumento similar permite demostrar que un 3-cap maximal tiene 9 puntos [3]. Sin embargo, esta técnica no sirve para demostrar que a₂ = 20, aunque se puede utilizar otra técnica habitual de Combinatoria, el conteo doble para demostrarlo [3].

Estas ideas que hemos trabajado en esta entrada son tan solo un primer acercamiento al estudio del problema geométrico relacionado con el juego SET generalizado, pero espero que nos hayan servido para que podamos hacernos una idea del tipo de matemáticas que están detrás del mismo.

Bibliografía

1.- Página web del juego SET en la empresa que lo ha comercializado en España, DEVIR

2.- Página web de la empresa SET Enterprises

3.- Benjamin Lent Davis y Diane MacLagan, The Card Game Set, The Mathematical Intelligencer 25, n. 3, p. 33-40, 2003.

4.- Giuseppe Pellegrino, Sul massimo ordine delle calotte in S_4,3, Matematiche (Catania) 25, p. 149-157 (1971), 1970.

5.- Y. Edel, S. Ferret, I. Landjev, L. Storme, The classification of the largest caps in AG(5,3), Journal of Combinatorial Theory A 99, p. 95-110, 2002.

6.- Aaron Potechin, Maximal caps in AG(6, 3), Designs, Codes and Cryptography 46, n. 3, 2008.

7.- Erica Klarreich, Simple Set Game Proof Stuns Mathematicians, QUANTA magazine, 31/05/2016

8.- M. Bateman, N. H. Katz, New bounds on cap sets, J. Math. Soc. 25, n.2, p. 585-613, 2012.

9.- Raúl Ibáñez, Las matemáticas de los juegos, RBA, 2014.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica