Cuando aprendemos a multiplicar durante la enseñanza primaria, primero tenemos que aprender las tablas de multiplicar, del 2 al 9 (las tablas del 0 y el 1 son triviales), para poderlas utilizar en el algoritmo estándar de multiplicación que nos enseñan cuando ya nos hemos aprendido las tablas. Y este ejercicio de memorización requiere de un gran esfuerzo por parte de los niños y niñas, lo que dificulta el aprendizaje y uso del método usual de multiplicación.

Aunque, como comentábamos en mi anterior entrada del Cuaderno de Cultura Científica, titulada ¿Sueñan los babilonios con multiplicaciones eléctricas?, peor lo tenían los babilonios que necesitaban utilizar las tablas de multiplicar del 2 al 59, debido a que el sistema de numeración babilónico era un sistema posicional sexagesimal, es decir, con base 60.

Sin embargo, la humanidad también inventó algunos métodos de multiplicación más sencillos, para los cuales únicamente se necesitaba saber multiplicar, y dividir, por 2.

El primero de esos métodos es el conocido como método de multiplicación egipcio, que tiene una antigüedad de más de 4.000 años.

Conocemos este sistema de multiplicación desarrollado por los egipcios gracias al Papiro matemático de Rhind, que es el documento matemático más importante conservado del Antiguo Egipto. Otros textos matemáticos egipcios son los papiros de Moscú, Lahún y Berlín.

El Papiro de Rhind, también conocido como Papiro de Ahmes, fue descubierto por el abogado y egiptólogo escocés Alexander Henry Rhind (1833-1863) en 1858, en Luxor (Egipto). El papiro fue copiado alrededor de 1650 a.c. por el escriba Ahmes, como él mismo indica al principio de la copia, de un texto anterior, de la época del faraón Amenemhat III (1860-1814 a.c.), que se perdió. El papiro tiene 33 cm de alto y está formado por varias partes, que en conjunto, adquieren una longitud de 5 m. Está redactado en escritura hierática y contiene más de 80 problemas, la mayoría de tipo práctico, con cuestiones aritméticas (multiplicación y división de números enteros y fracciones, fracciones unitarias o ecuaciones lineales), geométricas (áreas y volúmenes) y otras, entre las cuales están las progresiones aritméticas y geométricas, o las proporciones.

Antes de explicar en qué consiste el método de multiplicar egipcio, vamos a recordar el sistema de numeración que utilizaban los egipcios desde aproximadamente el 3.000 a.c, para poder describir el algoritmo de multiplicación teniendo en mente el sistema de numeración en el que fue creado.

Hacia el año 3.000 a.c., casi al mismo tiempo que los sumerios, los egipcios se inventaron un sistema de escritura, incluidos los números, jeroglífica, es decir, basada en sencillos dibujos o pictogramas. El sistema de numeración egipcio era decimal, esto es, en base 10, pero al contrario que el nuestro que es posicional, era un sistema aditivo, lo cual quiere decir que el 9 se representaba como nueve veces 1 o el 60 como seis veces 10. Como los egipcios representaban números más grandes que un millón, tenían pictogramas para 1, 10, 100, 1.000, 10.000, 100.000 y 1.000.000, que son las que aparecen en la imagen siguiente. El 1 se representaba con un trazo vertical, el 10 con una herradura, una “U” invertida, el 100 con una cuerda enrollada, una especie de espiral, el 1.000 con una flor de loto, incluido su tallo, 10.000 con un dedo levantado y torcido, 100.000 con un renacuajo y 1.000.000 con un hombre arrodillado y con los brazos levantados, que al parecer representaba al dios Heh, dios del infinito y la eternidad, sujetando el cielo.

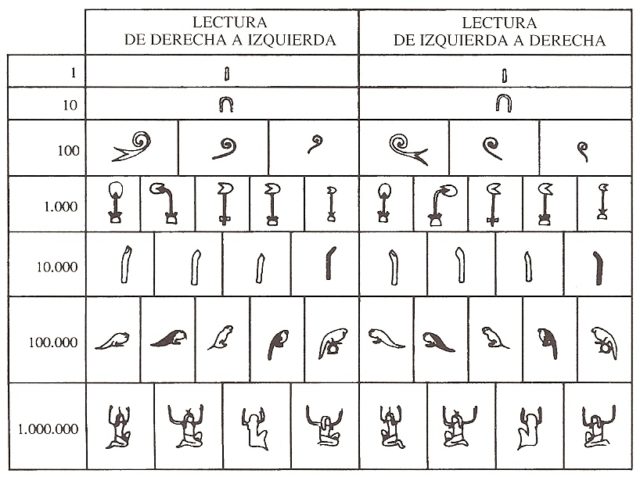
En el libro La cresta del pavo real se comenta que, aunque rara vez se utilizase, tenían un dibujo para los diez millones, 10.000.000, que era un sol, seguramente en referencia al dios egipcio Ra.

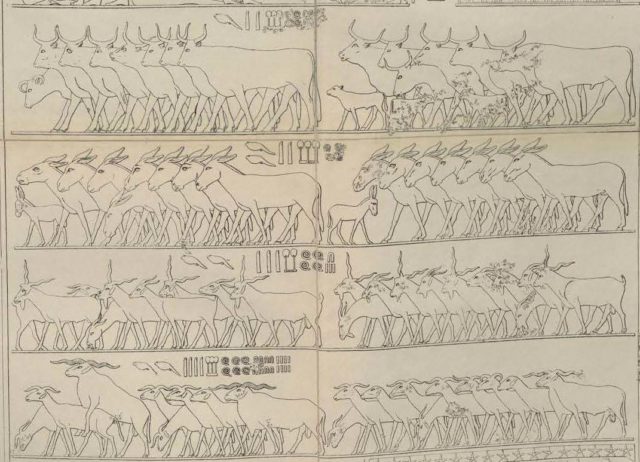
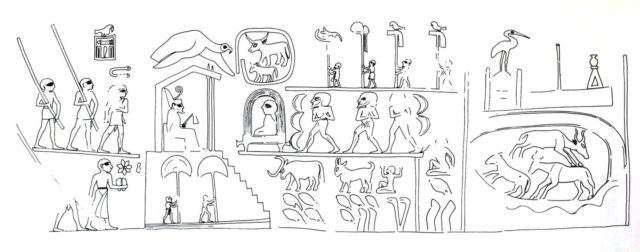
Para entender cómo escribían los egipcios los números de una forma acumulativa a partir de las cifras fundamentales anteriores vamos a utilizar un ejemplo real. En una de las inscripciones funerarias (véanse las siguientes imágenes) que el egiptólogo alemán Ludwig Borchardt (1863-1938) encontró en la pirámide de Sahure, segundo faraón de la quinta dinastía, hacia el 2.480 a.c., en la necrópolis de Abusis en Egipto, se realiza un recuento de más de 123.440 toros (los últimos pictogramas no se entienden bien, podrían ser más decenas o unidades), 223.400 burros, 32.413 cabras y 243.688 ovejas (?). Por ejemplo, esta última cantidad son dos renacuajos (200.000), cuatro dedos (40.000), tres flores de loto (3.000), seis cuerdas enrolladas (600), ocho herraduras (80) y ocho líneas verticales (8), luego 243.688.

Aunque el sistema de escritura (incluidos los números) jeroglífica daría paso a la escritura hierática (signos cursivos que permitían a los escribas realizar una escritura más rápida que teniendo que escribir los jeroglíficos), que es la escritura en la que está escrito el Papiro matemático de Rhind. Sin embargo, en esta entrada hablaremos solo del sistema de escritura jeroglífica en la explicación del método de multiplicar de los egipcios.

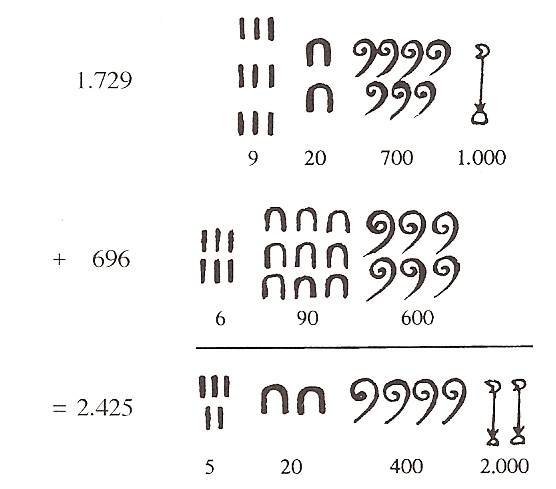
Puesto que el sistema de numeración egipcio era aditivo, es decir, funcionaba por acumulación de sus cifras, la suma era un proceso sencillo que consistía precisamente en acumular las cifras y reagrupar, es decir, cuando se tenían diez líneas verticales (1) se sustituían por una herradura (10) y lo mismo con el resto. Veamos un ejemplo, la suma de 1.729 y 696.

Pero vayamos ya con la multiplicación. Este sencillo método para multiplicar inventado por los egipcios, que se basa únicamente en las multiplicaciones por el número 2 (duplicaciones), se puede observar, por ejemplo, en el problema 32 del Papiro de Ahmes, donde se realiza la multiplicación 12 x 12, o en el problema 79, donde se multiplica 2801 x 7.

La mejor manera de explicar este método es a través de un ejemplo sencillo. Vamos a multiplicar 17 por 13. En la siguiente imagen está la multiplicación con la notación jeroglífica egipcia, a la izquierda, y con la notación moderna, a la derecha.

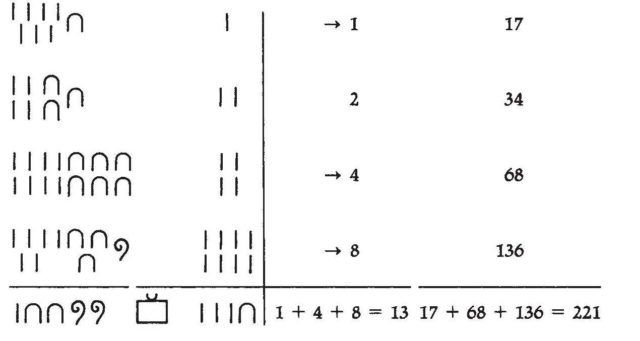
Para empezar, en este algoritmo para la multiplicación se van a escribir dos columnas de números, en la primera colocamos arriba el número 1 y en la otra uno de los números a multiplicar, en este ejemplo el 17. En la segunda fila multiplicamos por 2 los números de arriba, los de la primera fila, es decir, en la primera columna aparece el 2 y en la segunda 34, dos veces 17. En la tercera fila volvemos a multiplicar la anterior por 2, y obtenemos 4 y 68. Y en la cuarta, 8 y136. Es decir, en cada fila multiplicamos por 2 los números de la anterior.

En la primera columna, la que empieza por 1, se obtienen las potencias de dos, 1, 2, 4, 8, y podríamos seguir 16, 32, 64, 128, etc. si tuviésemos números más grandes, mientras que en la otra columna, la que tiene arriba el número que vamos a multiplicar (17), tenemos el resultado de multiplicar 17 por los números de la primera columna, 17, 34 = 17 x 2, 68 = 17 x 4 y 136 = 17 x 8.

Como queremos multiplicar el 17 por el número 13, y este se puede escribir como suma de algunos de números de la primera columna, 13 = 8 + 4 +1, entonces la multiplicación 17 x 13 será igual a la suma de los números de la columna derecha que se corresponden con 8, 4 y 1, es decir, 136 + 68 + 17 = 221. Esto no es más que una consecuencia de la propiedad distributiva.

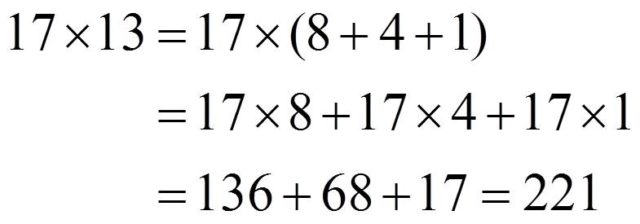
Como podemos observar, este método se basa en dos cuestiones que ya conocían los egipcios, que todo número se puede expresar como suma de distintas potencias de 2 (1 = 2⁰, 2 = 2¹, 4 = 2², 8 = 2³, 16 = 2⁴, 32 = 2⁵, 64 = 2⁶, 128 = 2⁷, etc) y la propiedad distributiva de la suma y el producto, (a + b) x c = a x c + b x c.

Veamos otro ejemplo. Imaginemos, como podría sugerir el historiador de las matemáticas George Ifrah la siguiente situación. Un “inspector de contribuciones” debía de contar cuántos sacos de cereal se habían recogido en una determinada zona de Egipto, si cada uno de los 419 campesinos de la zona debía de pagar un impuesto de 23 sacos de cereal.

Para calcular el número total de sacos de cereales que se han recaudado por los impuestos, el inspector realizaría la multiplicación 419 x 23 de la siguiente manera (en la imagen de abajo realizamos directamente la multiplicación con las cifras modernas). Escribiría dos columnas de números, la de la izquierda en la imagen con el 1 arriba y la de la derecha con el número multiplicador 23, y en cada fila se multiplicarían los números de la anterior por 2. En la columna de la izquierda aparecerían todas las potencias de 2 (en este caso, hasta 256) y en la columna de la derecha el resultado de multiplicar el 23 por los números de la izquierda, las potencias de 2, así 2 x 23 = 46, 4 x 23 =92, 8 x 23 = 184, 16 x 23 = 368, etc. Aunque no olvidemos que estos números los habría ido obteniendo simplemente por duplicación, al multiplicar los números anteriores por 2, 23 x 2 = 46, 46 x 2 = 92, 92 x 2 = 184, etc.

El siguiente paso sería marcar (con un guión) los números de la columna de la izquierda (que son las potencias de 2) que se necesitan para obtener el multiplicando, el número 419. En este ejemplo, 256, 128, 32, 2 y 1, puesto que 419 = 256 + 128 + 32 + 2 + 1.

Y finalmente, se sumarían los números de la columna de la derecha que se correspondían con las marcas, es decir, 5.888, 2.944, 736, 46 y 23, obteniéndose por lo tanto, que 419 x 23 = 5.888 + 2.944 + 736 + 46 + 23 = 9.637.

Con este método de multiplicar los egipcios estaban utilizando el germen del concepto de número binario, que no se introduciría formalmente hasta 1679, de la mano del matemático alemán Gottfried Leibniz (1646-1716). Si en la columna de la izquierda, con las potencias de 2, de la multiplicación egipcia, consideramos un 0 cuando no hay marca y un 1 cuando tenemos una marca, se obtiene la expresión binaria del número multiplicador, en los ejemplos anteriores, 13 y 23.

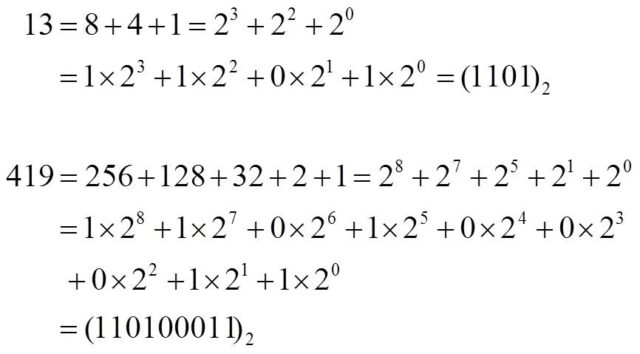
Además, los egipcios desarrollaron un método de división que no era más que el recíproco del algoritmo multiplicativo (que también aparece en el Papiro matemático de Rhind). Si se quiere realizar la división de 247 entre 13, se trata de utilizar el método anterior de las dos columnas para calcular “cuántas veces está 13 en 247”.

De nuevo, se escriben dos columnas de números por el método de multiplicar por 2 los números que están en la fila anterior, una columna con el 1 arriba y la otra con el divisor, 13 en este ejemplo, arriba. La diferencia está en que ahora, para saber “cuántas veces tenemos el 13 dentro de 247”, hay que escribir el dividendo, 247, como suma de los números de la columna de la derecha. En este caso, 247 = 208 + 26 + 13, pero ahora nos fijamos en los números correspondientes de la otra columna, la de la izquierda, 16, 2 y 1, ya que 208 = 13 x 16, 26 = 13 x 2 y 13 = 13 x 1, de donde se obtiene que la división de 247 entre 13 es 16 + 2 + 1 = 19.

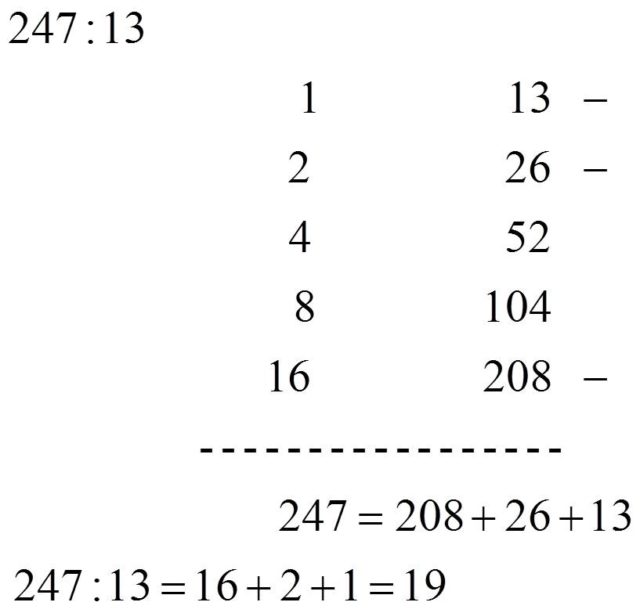
Este método de división egipcio era válido también para divisiones no exactas, aunque para ello había que manejar fracciones, y los egipcios eran unos expertos en las mismas. Veamos un sencillo ejemplo para que entendamos un poco cómo funcionaba la división no entera.

En el libro La cresta del pavo real se menciona que el método de multiplicación egipcio fue utilizado, con algunas variaciones, por los griegos y continuó utilizándose hasta la Edad Media en Europa.

El segundo método que vamos a mostrar en esta entrada, para el cual únicamente se necesitaba saber multiplicar, y dividir, por 2 (duplicación y mediación), es una variación del método egipcio, conocida como método de multiplicación de los campesinos rusos. El nombre se debe a que, según algunos textos, todavía es utilizado en algunas zonas rurales de Rusia. En el libro Excursions in Number Theory se narra cómo es utilizado en Etiopía, aunque allí se realiza con agujeros en el suelo y guijarros, y de hecho, este método también suele recibir el nombre de multiplicación etíope. Y he leído alguna referencia a que también podría seguir utilizándose en zonas rurales de Oriente Próximo.

Este método es muy sencillo también. De nuevo, veamos cómo funciona mediante un ejemplo. Primero, uno bastante sencillo.

Multipliquemos 643 por 32. Como en el método anterior, se van a escribir dos columnas de números, cada una de las cuales tiene arriba a uno de los números que queremos multiplicar, 643 y 32. Debajo de estos números escribiremos, en la columna de la izquierda la multiplicación del anterior número por 2, 643 x 2 = 1.286, y en la columna de la derecha la división del anterior número por 2, 32 : 2 = 16. Es evidente, que si multiplicamos al primer número, 643, por 2 y dividimos al segundo número, 32, por 2, el producto de los dos nuevos números es el mismo. Es decir, 643 x 32 = 1.286 x 16.

En la siguiente fila, la tercera, volveremos a multiplicar por 2 en la columna izquierda, 1.286 x 2 = 2.572, y a dividir por 2 en la derecha, 16 : 2 = 8. Y el producto sigue inalterado, es decir, 643 x 32 = 1.286 x 16 = 2.572 x 8. Continuamos esta doble operación, multiplicación y división por 2 (duplicación y mediación), hasta que en la columna de la derecha llegamos a 1, y nos fijamos en el número que le acompaña a la derecha, 20.576, que será el resultado de multiplicar 643 por 32.

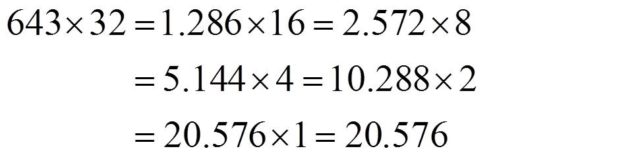
Aunque, evidentemente, este método tiene el problema de que si el número de la derecha es impar, en alguno de los pasos, no se va a poder dividir por 2. El método de multiplicación de los campesinos rusos, también llamado etíope, precisamente explica cómo realizar la multiplicación en el caso general.

De nuevo, utilicemos una multiplicación concreta para ver cómo funciona el método en general. Multipliquemos 517 por 43.

Puesto que el 43 no es par, lo que se hace es restar uno a ese número, 43 – 1 = 42, colocamos un 1 entre paréntesis al lado (como se muestra en la imagen de arriba), para saber que ahí ha quedado una unidad sin multiplicar al 517 y dividimos 42 entre 2, escribiendo el resultado, 21, abajo en esa columna de la derecha (como en la imagen). Y en la izquierda habremos multiplicado por 2, obteniendo 1.034.

Tengamos en cuenta que al restar 1 lo que estamos haciendo es quitándole a la multiplicación que estamos realizando la cantidad de 517, luego al final habrá que añadirla.

A continuación, tenemos el 21, que de nuevo es impar, por lo que le restamos 1, indicándolo con un 1 entre paréntesis (como en la imagen), y dividiendo 20 por 2, es decir, 10. Al mismo tiempo en la columna de la derecha se habrá vuelto a multiplicar por 2 y escribimos el resultado, 2.068. El 10 es par, por lo que lo dividimos entre 2, obteniendo 5, y su pareja de la izquierda la multiplicamos por 2, 2.068 x 2 = 4.136. Y así continuamos hasta alcanzar el 1 en la columna de la derecha.

En consecuencia, el producto de 517 por 43 será igual a 16.544, que es el número a la izquierda del 1, más las cantidades que hemos quitado al ir restando 1 en la columna de la derecha, una vez 517, una vez 1.034 y una vez 4.136. En total,

Veamos otro ejemplo del método de multiplicar de los campesinos rusos, que nos permita comprobar que hemos entendido este sencillo algoritmo, para el cual solamente es necesario saber multiplicar y dividir por 2, además, por supuesto, de saber sumar.

Para cerrar el artículo, un par de imágenes de números jeroglíficos egipcios.

Bibliografía

1.- Georges Ifrah, Historia universal de las cifras, Espasa, 2002.

2.- Lucas N. H. Bunt, Philip S, Jones, Jack D. Bedient, The Historical Roots of Elementary Mathematics, Dover Publications, 1988.

3.- George Gheverghese Joseph, La cresta del pavo real, las matemáticas y sus raíces no europeas, Pirámide, 1996.

4.- The Rhind Mathematical Papyrus (British Museum 10057, 10058), Mathematical Association of America, 1927.

5.- Ludwig Borchardt, Das Grabdenkmal des Königs S’ahu-Re, Hinrichs, Leipzig, 1919.

6.- C. Stanley Ogilvy, John T. Anderson, Excursions in Number Theory, Dover Publications, 1988.

7.- David M. Burton, The history of mathematics, an introduction, McGraw Hill, 2011.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica