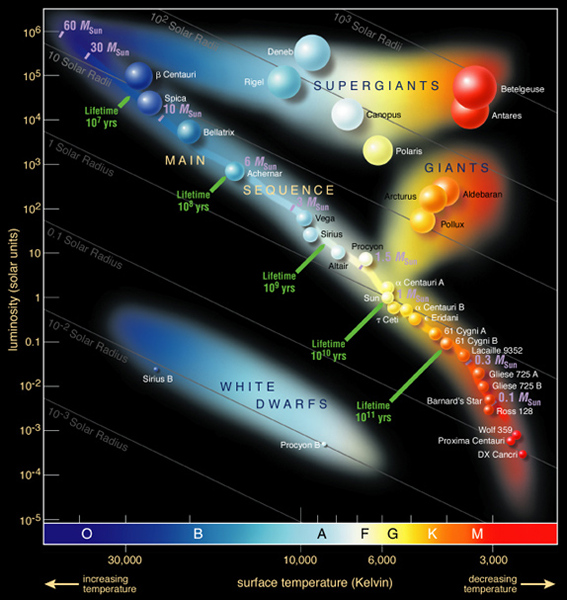
El diagrama HR es una de las herramientas más potentes y más empleadas en el estudio de la física estelar. A pesar de su simplicidad contiene cantidad de información relevante acerca de las estrellas.

El objetivo de esta contribución al Cuaderno de Cultura Científica es el de explicar cómo se construye este diagrama y cómo se ha de leer. Esto permitirá a cualquiera intuir la potencia de esta herramienta y a marcarse un tanto en una discusión con familiares y amigos. Así que lee y divulga.

Este diagrama fue definido por Ejnar Hertzprung en 1911 y de forma independiente por Henry Norris Russel en 1913. Gracias a sus trabajos disponemos de esta hermosa y útil herramienta para el estudio de las estrellas.

La luz, oui c’est moi

Para empezar por el principio diremos que la luz es una onda electromagnética. Gracias a los trabajos de Maxwell entendimos que la luz no es más que campos eléctricos y magnéticos variables en el tiempo en forma ondulatoria que se propagan incluso por el vacío.

Como toda buena onda, una onda electromagnéticia se caracteriza por varios parámetros. Los que nos interesan aquí son la longitud de onda, la frecuencia y su velocidad de propagación. La velocidad de propagación de una onda electromagnética en el vacío es justamente la velocidad de la luz, redondeando unos 300000km/s. La frecuencia es el número de oscilaciones que realizan el campo eléctrico o magnético en un punto del espacio por el que está pasando una onda electromagnética. La longitud de onda, por su parte, es la distancia entre dos picos de la onda tal y como se ve en la figura 2.

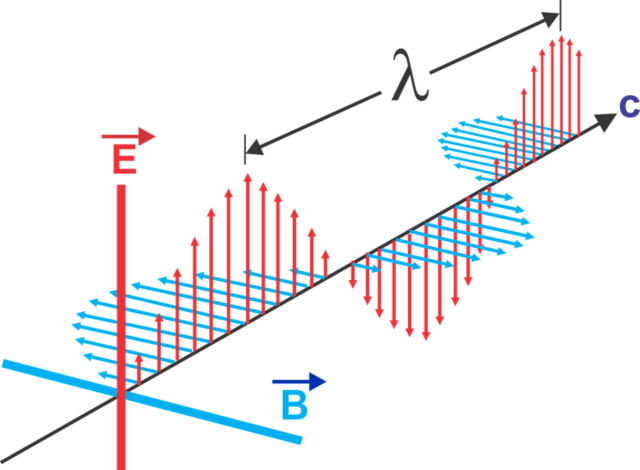
Estos tres parámetros no son independientes entre sí. Si denotamos la velocidad de las ondas electromagnéticas en el vacío por c, la frecuencia por f y la longitud de onda por λ, se ha de cumplir:

c=f·λ

Dado que la velocidad de la luz en el vacío es una constante, según dictamina la relatividad, conocida la frecuencia o la longitud de onda podemos determinar el valor de la otra.

Esta característica nos permite hacer una clasificación de las ondas electromagnéticas en términos del valor de su longitud de onda. Esta clasificación se denomina el espectro electromagnético:

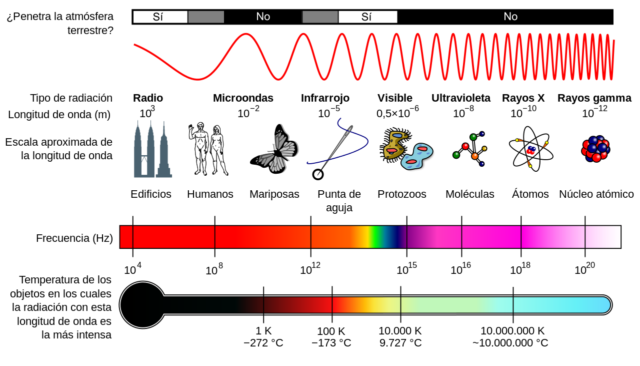
Así cuando nos hablan de ondas de radio, mircoondas, infrarrojo, luz visible, ultravioleta, rayos X o rayos gamma, en realidad nos están hablando de los rangos de longitudes de onda de la radiación electromagnética que estemos considerando.

Todas esas ondas electromagnéticas serán referidas simplemente como luz. Usualmente luz hace referencia a la parte del espectro electromagnético que somos capaces de percibir, la luz visible, pero en este caso usaremos indistintamente radiación electromagnética o luz en un sentido amplio.

Color y temperatura

Todos tenemos una constancia más o menos cotidiana del cambio de color que se produce en los materiales cuando estos se calientan. Todos hemos visto ponerse un metal al rojo vivo al aumentar su temperatura, por ejemplo en la resistencia de una estufa eléctrica. Este hecho es una consecuencia directa de las leyes del eletromagnetismo y la termodinámica operando a escalas cuánticas. Cuando calentamos un material estamos inyectando energía en el sistema. Esta energía hace que los átomos que conforman el material se exciten de múltiples y variadas maneras y comiencen a intentar reducir su energía emitiendo radiación electromagnética. Por lo tanto, por el simple hecho de tener una determinada temperatura un cuerpo está emitiendo radiación electromagnética.

Ocurre que el material emite en todas las longitudes de onda. Lo interesante es que podemos medir la cantidad de energía emitida en cada longitud de onda. En la figura 4 tenemos justamente la gráfica que nos da la cantidad de energía, que vamos a llamar luminosidad, emitida por cada longitud de onda para un cuerpo ideal, un cuerpo negro, que está a 4000K. Recordemos que el Kelvin, K, es una unidad absoluta de temperatura, es decir, el 0K es el cero absoluto de la temperatura y la termodinámica nos dice que no podemos llegar a esa temperatura por ningún proceso físico. 0K equivale a -273.15ºC.

Pero veamos la figura 4:

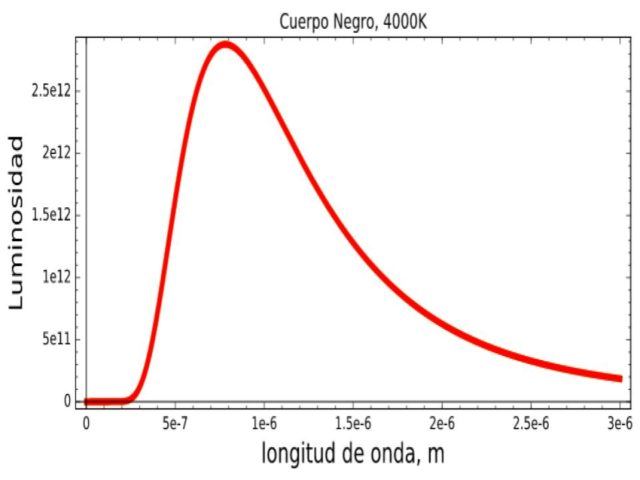
Lo primero que ha de quedar claro aquí es cómo leer esta gráfica. Lo que indica cada punto de la curva roja es la cantidad de energía, luminosidad o brillo, que tiene el cuerpo a 4000K en cada longitud de onda. Eso es lo que se refleja en la figura 5.

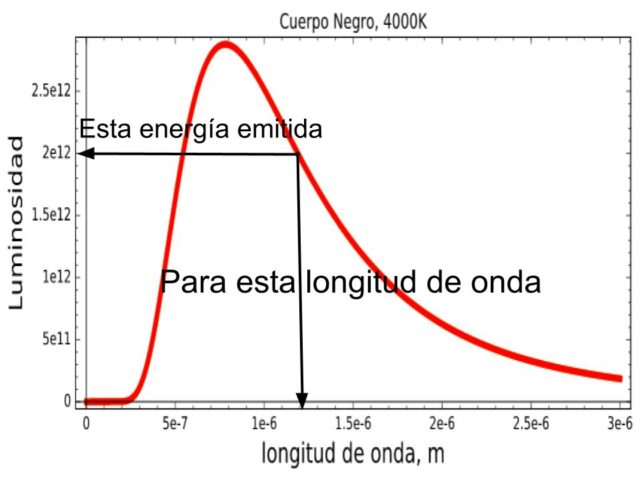
Lo que está claro de la figura 4 es que hay una longitud de onda, λmax, para la que hay un pico en la emisión del cuerpo, es decir, donde hay un máximo en la curva. Luego vemos que para longitudes de onda más cortas la emisión decrece muy rápidamente y para longitudes de onda más largas también decrece aunque de un modo más suave.

Una propiedad interesante de esta gráfica es que la longitud de onda para la que tenemos el máximo de luminosidad, brillo o energía emitida, la λmax, está relacionada de forma simple con la temperatura del cuerpo:

λmax= b/T,

donde T es la temperatura del cuerpo en Kelvins y b es una constante que toma por valor 0.0029 m·K (metros por Kelvin). Eso quiere decir que si conocemos la temperatura de un cuerpo podremos decir en qué longitud de onda emitirá preferentemente.

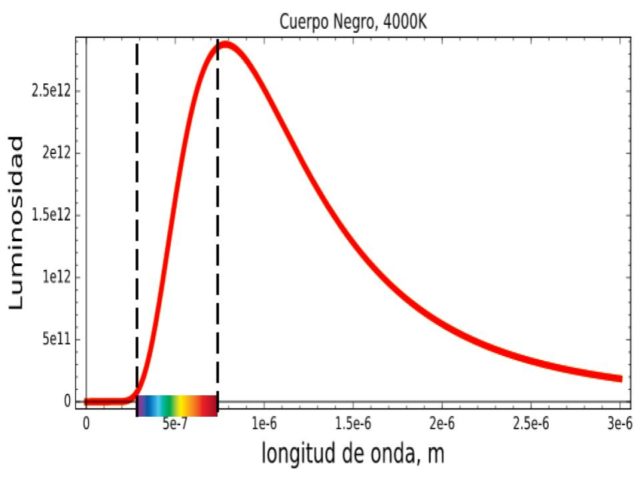
Si recordamos que las longitudes de onda nos permitían clasificar las ondas electromagnéticas resulta que sabremos en qué región del espectro electromagnético emite un determinado cuerpo. Para el caso de la figura 4 podemos introducir la parte visible del espectro electromagnético y observar que ese cuerpo nos parecerá que empieza a ponerse rojizo tal y como se indica en la figura 6.

Pero otro hecho interesante es que si aumentamos la temperatura de este cuerpo hasta los 5000K veremos que la longitud de onda para la que se alcanza el máximo de emisión se desplaza a longitudes de onda más cortas. Esto se representa en la figura 7:

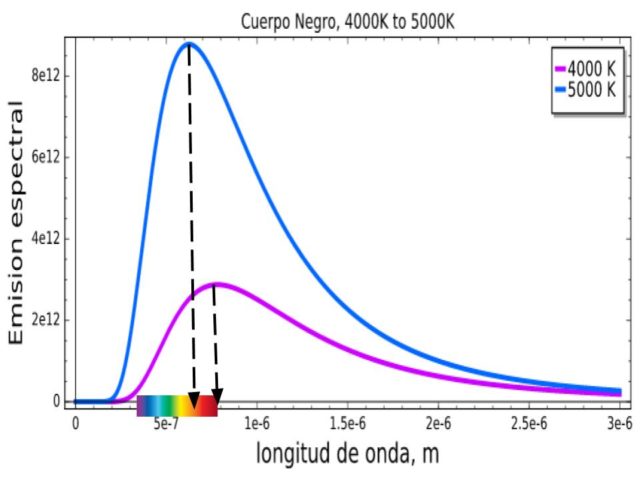
Observen que si aumentamos la temperatura el cuerpo emite más en general. Es lógico, le estamos comunicando más energía por lo que tiene más energía que emitir. Pero vemos como el pico se desplaza a una longitud de onda más corta. En el caso representado en la figura el cuerpo está emitiendo ya en una longitud de onda correspondiente al amarillo/naranja. Así que ese cuerpo, en total oscuridad, lo veríamos brilla con un color amarillento-anaranjado. Por lo que hemos encontrado una bonita relación entre la temperatura de un cuerpo y el colo con el que brilla.

Así que, si conocemos el color con el que brilla un cuerpo podremos determinar su temperatura sin problemas. No se te habrá escapado la relación que tiene esto con la determinación de la temperatura de estrellas. Si ahora te dan un puñado de estrellas seguro que eres capaz de ordenarlas en temperaturas crecientes o decrecientes, figura 8.

Luminosidad

No hemos acabado de sacarle el jugo a esta gráfica de emisión de energía electromagnética por cada longitud de onda. Aún depara una sorpresa más y esta lleva por nombre: Ley de Stefan-Boltzmann.

Esta ley es asombrosa porque de una forma muy simple es capaz de decirnos cuánto emite un cuerpo por unidad de área al estar a una determinada temperatura. Para ello vamos a definir los siguientes elementos:

1.- F = Energía radiada por cada metro cuadrado del cuerpo que estemos estudiando y por cada segundo. Se la suele denominar flujo de energía.

2.- T = Temperatura a la que está el cuerpo en Kelvins.

3.- ? = Constante de Stefan que tiene por valor 5.67·10^-8 W/(m²K⁴).

Resulta que la energía radiada por metro cuadrado y segundo, es decir, la potencia en watios (W) por unidad de área, se puede calcular con esta simple fórmula:

F=?T⁴

Por tanto, la potencia emitida por unidad de área se puede calcular a partir de tan solo la temperatura. Basta elevar la temperatura a la cuarta potencia y multiplicarla por la constante de Stefan. Eso nos da la energía por unidad de área.

A partir de aquí es fácil definir la luminosidad de un cuerpo ya que solo hay que multiplicar F por el área total del cuerpo. Dado que aquí nos interesan las estrellas y estas suelen ser esferas en primera aproximación, recordando que el área total de una esfera es 4πR², donde R es el radio de la estrella, la luminosidad L se define como:

L=4πR²·F=4πR²?T⁴

Si agrupamos todas las constantes nos queda:

L=(4π?)R²T⁴

Por lo que la luminosidad de una estrella depende de su radio (al cuadrado) y de su temperatura (a la cuarta). Lo que resulta una relación muy útil en astrofísica estelar.

Diagrama HR

Intentemos construir el diagrama HR por nuestros propios medios ya que hemos consumido un poco de tiempo entendiendo sus fundamentos aunque no nos hayamos dado cuenta.

A lo tonto hemos encontrado una relación entre luminosidad y temperatura. Así que lo lógico es poner un eje para la luminosidad y otro para la temperatura.

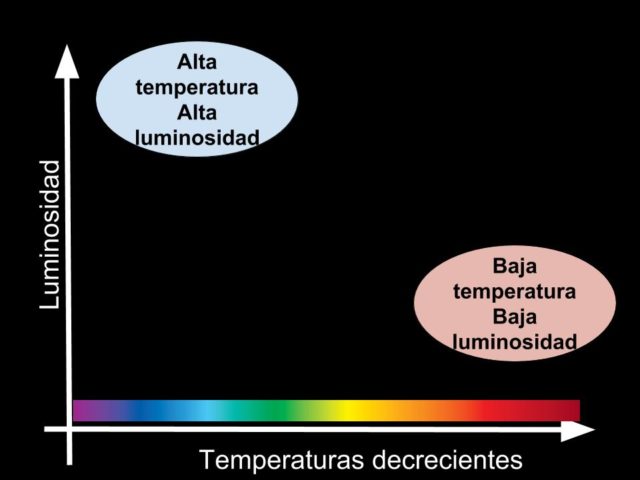
Lo primero que podemos decir a la vista de los ejes, observad que las temperaturas decrecen hacia la derecha en contra del sentido “natural”, es dónde están las zonas de estrellas luminosas de alta temperatura y estrellas poco luminosas de baja temperatura.

También nos podemos permitir utilizar la relación entre la temperatura de un cuerpo, una estrella en nuestro caso, y el color donde emite el máximo de energía.

Y por supuesto, dado que L y T se relacionan a través del radio R de la estrella como hemos visto, podemos dar la posición de los distintos radios posibles para las estrellas.

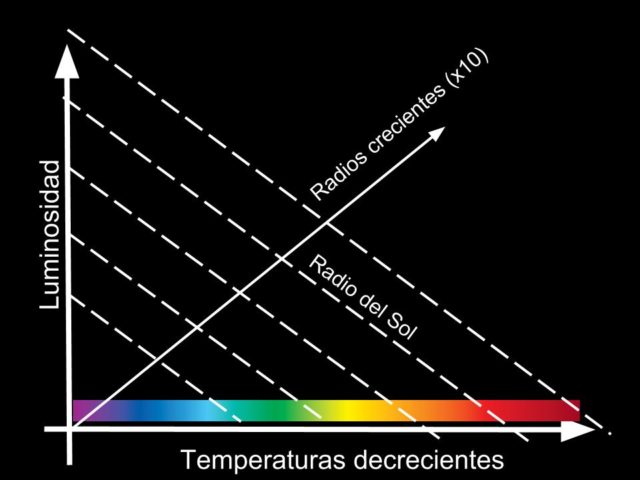
Esta relación nos dice que dos estrellas con la misma luminosidad pero temperaturas diferentes han de tener radios diferentes. Si la emisión de energía total es la misma, la luminosidad, pero una tiene una temperatura menor que la otra ha de ser porque tiene un radio mayor que la otra respectivamente. Por contra, si dos estrellas tienen la misma temperatura pero distinta luminosidad, la que tiene mayor luminosidad ha de tener mayor radio. Eso es lo lógico, porque si tiene la misma temperatura pero está emitiendo una cantidad mayor de energía total es porque la estrella ha de ser más grande. Esto que estamos diciendo en palabras no es más que moverse en horizontal o vertical por el diagrama. Prueba a pensarlo de ese modo y a ver qué concluyes.

Ahora respondamos a esta pregunta, ¿dónde situaríamos las distintas estrellas?

Pues eso se responde del siguiente modo:

1.- Las estrellas de baja temperatura y alta luminosidad estarán en la esquina superior derecha. Eso implica que serán estrellas de un radio grande. En esa zona es fácil que encontremos las gigantes rojas.

2.- Por la esquina inferior izquierda encontraremos estrellas pequeñas de alta temperatura y baja luminosidad. Por ejemplo, enanas blancas.

3.- Las estrellas de luminosidades, radios y temperaturas intermedias estarán por el centro del diagrama.

Lo asombroso es que cuando ponemos las estrellas en este diagrama parecen seguir un patrón definido:

Vemos que nuestras intuiciones, que hemos adquirido a través de estudiar la relación entre color, energía emitida y temperatura, se verifican. Pero observamos que las estrellas no se diseminan por el diagrama sino que siguen un camino, denominado secuencia principal, o se agrupan en algunas regiones, la de las enanas blancas o la de las gigantes y supergigantes.

Eso es lo que convierte a este diagrama, además de todo lo anterior, en una poderosa herramienta. Estas agrupaciones tan nítidas de las estrellas en el diagrama sugiere que las estrellas tienen un ciclo de vida estelar y que se van “desplazando” por el diagrama en las distintas fases de su evolución. Así, nuestro Sol que está en la parte intermedia, con el paso del tiempo irá consumiendo completamente su combustible nuclear y se irá expandiendo y enfriando, se convertirá en una gigante roja y por tanto subirá por la secuencia principal hasta entrar en la rama de gigante roja.

Gracias al diagrama, los astrofísicos estelares pueden estimar las masas de las estrellas y por tanto su tiempo de vida. Sin duda, este es un ejemplo de la poderosa e inquietante simplicidad de la naturaleza, aunque no siempre sea el caso.

Espero que ahora estos diagramas tengan más sentido y que esta entrada os permita profundizar en este hermoso apartado de la física estelar.

Nos seguimos leyendo…

Este post ha sido realizado por Enrique F. Borja (@Cuent_Cuanticos) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.