Mai quai Contii de Michèle Audin es –como la propia autora dice en su prefacio– un homenaje a la Comuna de Parísii en el que se mezcla ciencia, historia y literatura:
- ciencia porque los trece capítulos –sin contar el prefacio y el epílogo– corresponden a trece fechas de 1871, que coinciden con trece sesiones de l’Académie des sciencesiii que tenían lugar los lunes por la tarde,
- historia porque trata de un momento crucial en la historia del pueblo francés: los sesenta días de gobierno de la Comuna, detallándose lo que sucedió en el terreno revolucionario, político y cultural en París, y
- literatura porque –además de las muchas referencias literarias que pueden leerse– Michèle Audiniv escribe este texto bajo trabas oulipianas –usa pastiches, tautogramas, monovocalismos, lipogramas, etc.–, y presentando una restricción creada por ella misma, la traba de Pascal –explicada con detalle en el epílogo y en el índice– que le permite organizar los capítulos como explicaremos a continuación.
Cada capítulo corresponde a un lunes, una fecha de reunión de l’Académie des Sciences. La autora narra con detalle los temas que se trataron en aquellas reuniones, tanto de tipo científico, como político o cultural. Cada fecha –cada sesión, cada capítulo– va acompañada de una figura geométrica –una elipse– con varios puntos marcados sobre ella y segmentos relacionando algunos de esos puntos. Estos nexos entre puntos van cambiando de capítulo en capítulo, al incorporar nuevos personajes o situaciones; pero aún más: cada fecha corresponde a un paso de la demostración del teorema de Pascal tal y como lo prueba la propia autora en su libro [Michèle Audin, Géométrie, Edp-Sciences, 2006, segunda edición].
El teorema de Pascalvi es un enunciado de geometría proyectiva que dice –el enunciado y la prueba son los que Michèle Audin utiliza en el texto–:
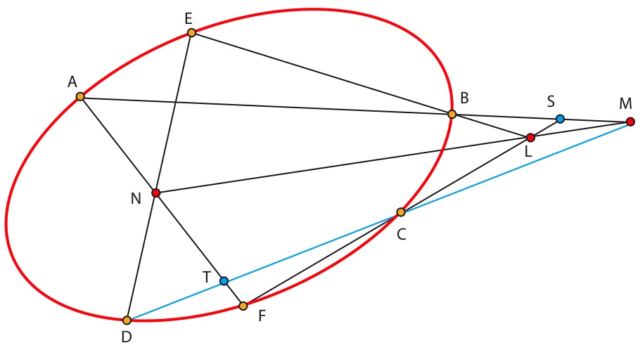
Sea C una cónica propia de imagen no vacía y sean A, B, C, D, E y F seis puntos sobre esta cónica. Sean N=(AF)∩(ED),M=(AB)∩(CD) y L=(CF)∩(EB). Entonces los puntos L, M y N están alineados.
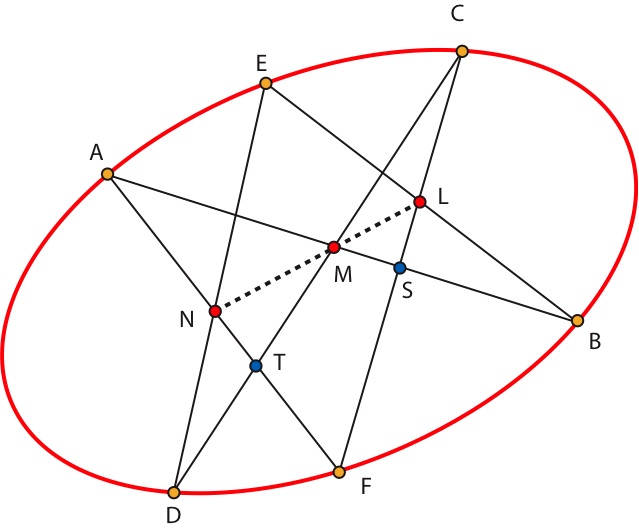
Demostraciónvii:
Sean S=(AB)∩(CF)yT=(CD)∩(AF). Se tiene queviii
[S,L,C,F]=[BS,BL,BC,BF]=[BA,BE,BC,BF]=[DA,DE,DC,DF]=[A,T,N,F].
Sea K=(LN)∩(AB). La perspectividad de centro K que envía CF sobre AF ,envía S sobre A, L sobre N y F sobre F. La imagen de C es entonces T. Así K ∈ CT, es decir CD. Por lo tanto K=M. CQD
Esta demostración va a ser la que estructure cada capítulo, es decir, el enunciado junto a su prueba, divididos en trece pasos, establecerán personajes y relaciones.
—oOo—
13 DE MARZO
SEA C UNA CÓNICA PROPIA DE IMAGEN NO VACÍA
(en este caso C es una elipse)
Michèle Audin comienza su historia el 13 de marzo de 1871, describiendo el Mai quai Conti –sede de l’Académie des sciences– de manera exhaustiva, sin olvidarse de hablar de elipses, semicírculos, hélices, etc. La autora se pregunta sobre lo que podría estar sucediendo, sobre qué conversaciones se estarían manteniendo –el ejército prusiano acechando, posiciones políticas, etc.–, sobre lo que hicieron los académicos antes de llegar a la reunión, que calles atravesaron para llegar a la Academia desde sus casas… A través de los documentos archivados en la Academia, se puede saber quienes asistieron a cada reunión, los temas que trataron, las discusiones mantenidas, el tiempo que estuvieron reunidos, y todo tipo de detalles recogidos en las actas… hablaron de ciencia, de la situación política, de la visita de personajes del ámbito científico o literario, etc.
Este capítulo se presenta con la figura de una elipse –de la que habla también al describir el edificio, comentando que las cónicas eran muy valoradas por los arquitectos de la época–, que se irá completando durante el relato –como ya hemos comentado– añadiendo puntos y segmentos uniéndolos a medida que la narración progrese y los personajes se vayan relacionando.
Se habla, por ejemplo, del matemático Camille Jordan y su artículo Sur la résolution des équations les unes par les autres, más extenso que la media habitual de notas, pero que se publicaría de cualquier modo en el volumen 72 de los Comptes rendus de la Academia.
—oOo—
20 DE MARZO
Y SEAN A, B, C, D, E Y F SEIS PUNTOS SOBRE ESTA CÓNICA.
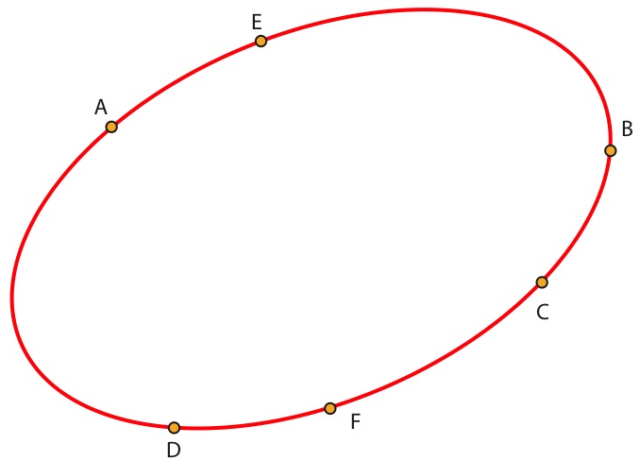
La autora presenta a seis de los personajes –su aspecto, sus posiciones políticas y sociales, sus vidas y algunas de sus aportaciones a la ciencia– que participaron en la reuniones durante el mes de marzo y coloca seis puntos en la elipse –que permanecerán durante toda la historia–: Charles Hermite (A), Joseph Bertrand (B), Michel Chasles (C), Charles Delaunay (D), Léonce Élie de Beaumont (E) y Hervé Faye (F). Describe de manera exhaustiva lo sucedido en la reunión, comentando en particular una visita de Victor Hugo a París para enterrar a su hijo brutalmente asesinado en las revueltas.
—oOo—
27 DE MARZO
SEAN N=(AF)∩(ED),
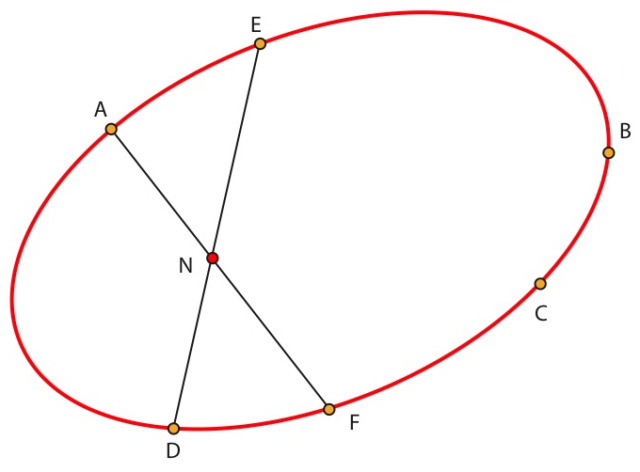
El astrónomo y geómetra Simon Newcomb (N) visita París para realizar observaciones y cálculos en l’Observatoire. Aunque no se sabe si encontró a Hermite (A) o Faye (F) –Hermite, el matemático principal y Faye, astrónomo– la autora comenta que probablemente ellos quisieron conocer al americano, y juega con la (A) de Hermite y la (F) de Faye a través de un divertido tautograma –este juego se repetirá en cada punto de intersección–:
Simon Newcomb, astronome américain, amateur d’algèbre, actif et aguerri, accueilli par l’Académie et accoutumé à ses alentours, affolé par l’ampleur de l’anarchie, accablé, familier de Faye, aux peu fictives facilités, fuyant frileusement la foison des fédérés faméliques, les farandoles de farouches fantassins fourbus, les fangeux et funestes faubourgs, fuyant la France.
colocando a Newcomb (N) en el punto medio del segmento que une (A) y (F).
Newcomb debía conocer a Delaunay (D) –gran especialista sobre la Luna y sus movimientos– y en vez de entregar a Léonce Élie de Beaumont (E) –el Secretario Perpetuo– el documento con sus medidas, lo llevó a la reunión del 3 de abril para terminar de redactar y completar su texto. La autora traza el segmento entre Delaunay (D) y Élie de Beaumont (E) –que como debía ser, pasa por (N)–, y dedica otro tautograma –esta vez en D y E– a Newcomb.
Hablando de la luna, se cita entre otros al astrónomo y matemático Urbain Le Verrier y al escritor Jules Verne. Y también aparecen destacados matemáticos –y alguna de sus aportaciones– como Joseph Liouville o Augustin Louis Cauchy.
—oOo—
3 DE ABRIL
M=(AB)∩(CD),
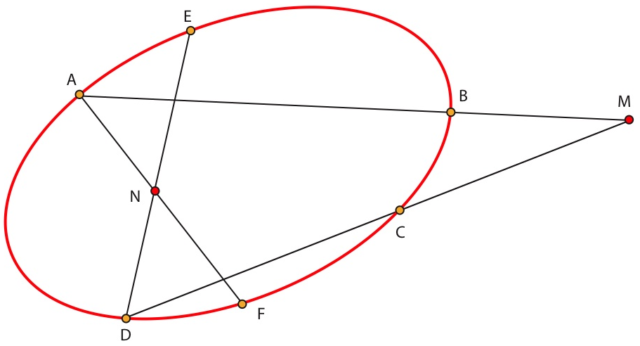
Un nuevo punto aparece –M, de‘moi’, la narradora– en la figura que rige el teorema de Pascal: Madame Hermite, la esposa de Charles Hermite (A) era hermana de Joseph Bertrand (B), aunque los dos científicos nunca llegaron a entenderse. Chasles –autor del Traité des coniques– y Delaunay estaban unidos por la Luna. Así. la (M) se genera a partir de la (A) y la (B), o a partir de la (C) y la (D).
La narradora –el yo, moi, que aparece–, confiesa mirar a Hermite (A) y Bertrand (B) y admirar a Chasles (C) y Delaunay (D), y lo expresa a través de un tautograma en A y en B… seguido de otro en C y D.
La autora realiza además un precioso homenaje al conocido Je me souviens de Georges Perec… con recuerdos sobre literatura, sobre derechos de las mujeres reconocidos por la Comuna, etc., transmitiendo lo vivido en París durante el mandato de la Comuna. Además, como ‘matemática y preocupada de elevar el nivel científico y cultural de sus lectores’, la narradora se permite aclarar algunos de los puntos matemáticos tratados en esta sesión de la Academia.
—oOo—
10 DE ABRIL
Y L=(CF)∩(EB).
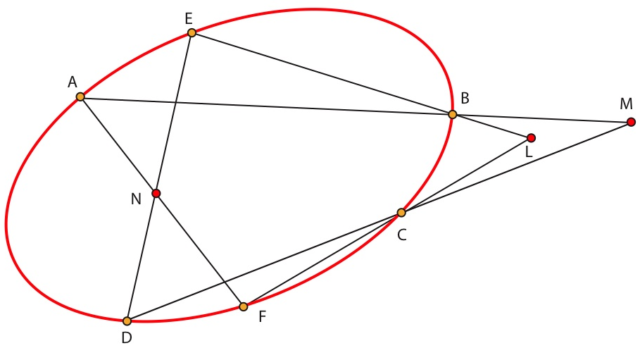
Aparece en la historia el periodista Prosper-Olivier Lissagaray (L), testigo de los acontecimientos y autor de Histoire de la Commune de 1871, publicado en 1896. Lissagaray no habría oído –probablemente– nunca hablar de Chasles (C) ni de Faye (F) –un tautograma en C y F le describe– pero habló en sus publicaciones de Bertrand (B) y de Élie de Beaumont (E) –otro tautograma en B y E sirve para trazar mejor a este personaje–.
Gustave Flourens es miembro de la Comuna y Lissagaray habla en particular de él y de su asesinato.
En la sesión de la Academia se habla de botánica, y Chasles continúa demostrando teoremas sobre cónicas.
—oOo—
17 DE ABRIL
ENTONCES LOS PUNTOS L, MY NESTÁN ALINEADOS.
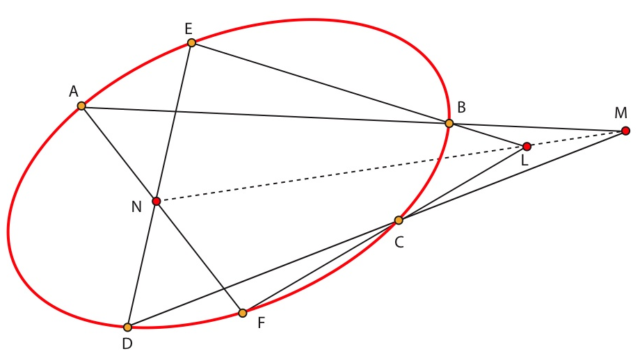
Con esta declaraciónix:
Qui suis-je, moi ? Qui suis-je, pour pouvoir raconter cette histoire ? Parler en même temps, presque d’une même phrase, de Prosper-Olivier Lissagaray et de Simon Newcomb ?
se traza una línea discontinua –que desaparecerá en el siguiente capítulo, ya que es el enunciado que se desea probar– entre la narradora (M), Lissagaray (L) y Newcomb (N). Un ‘tautograma’ mezclando la L con la N permite seguir la descripción del periodista y el científico.
Aparece –entre otras– una fotografía de Sofía Kovalevskaya, que habla de cómo está asistiendo a un momento histórico en París, de cómo ayuda a cuidar a los heridos y de su asistencia a las sesiones de la Academia.
—oOo—
24 DE ABRIL
SEAN S=(AB)∩(CF) Y T=(CD)∩(AF).
(comienza la demostración del teorema)
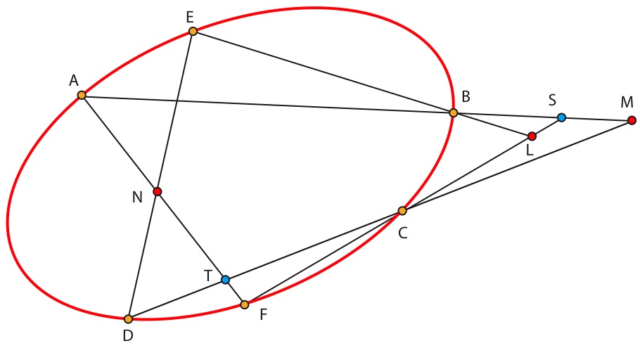
Desaparece la línea discontinua uniendo N, L y M –este es el comienzo de la demostración del teorema de Pascal, que dice precisamente que esa línea existe– y aparecen dos nuevos puntos: T y S.
(S) es el secretario secreto –que relata las sesiones de la Academia en elJournal Officiel de la Commune– no ha visto en esta sesión ni a Hermite (A) ni a Bertrand (B), pero si a Chasles (C) y no a Faye (F). Se trazan los segmentos entre A y B –que también pasa por M– y entre F y C –que también pasa por L–, que se cortan en S, y nuevos tautogramas en A y B y en F y C ayudan a describir al secretario.
Se habla en particular de cómo ‘gente loca’ envía demostraciones –por ejemplo del teorema de Fermat a la Academia–; así (T) representa tanto a este periodista que firma de manera anónima como a todos los que escriben a l’Académie des sciences con locas demostraciones y absurdos comentarios: T pasa por el segmento que une A y F –que pasa por N– y por el segmento que une D y C –que pasa por M–: los tautogramas en A, F, D y C ayudarán a describirlos.
… Y Chasles continúa con sus demostraciones sobre cónicas.
—oOo—
1 DE MAYO
SE TIENE QUE [S,L,C,F]=[BS,BL,BC,BF]
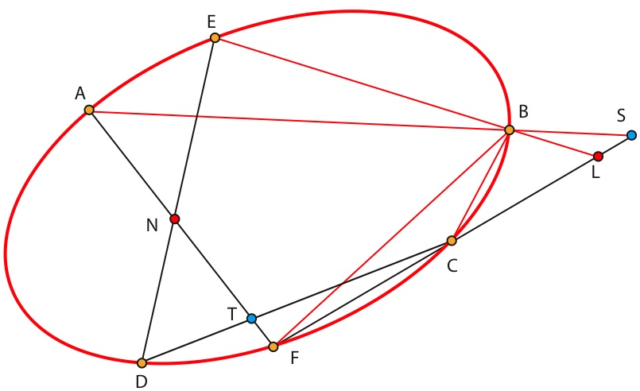
En la cónica desaparece M, la narradora; la de hoy es una jornada de caos, de dura batalla en la calle y de fusilamientos. Se relaciona a Bertrand (B) –que no ha acudido a la sesión de la Academia, y de diversas maneras– con el secretario secreto (S), con Lissagaray (L), con Chasles (C) y con Faye (F).
—oOo—
8 DE MAYO
=[BA,BE,BC,BF]=[DA,DE,DC,DF]
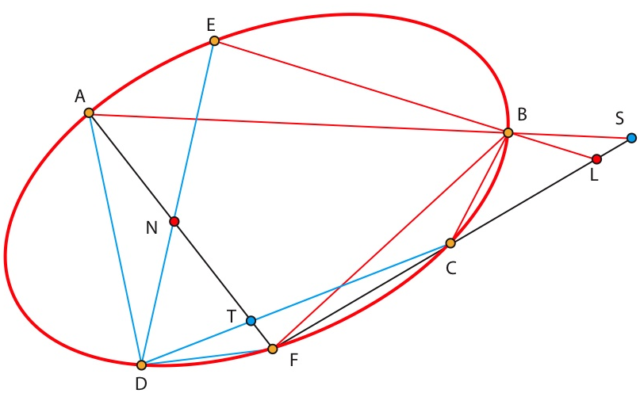
El 8 de mayo, Bertrand participa en la sesión de la Academia. No estaban ni Hermite (A) ni Faye (F), pero si Élie de Beaumont (E) y Chasles (C).
—oOo—
15 DE MAYO
=[A,T,N,F].
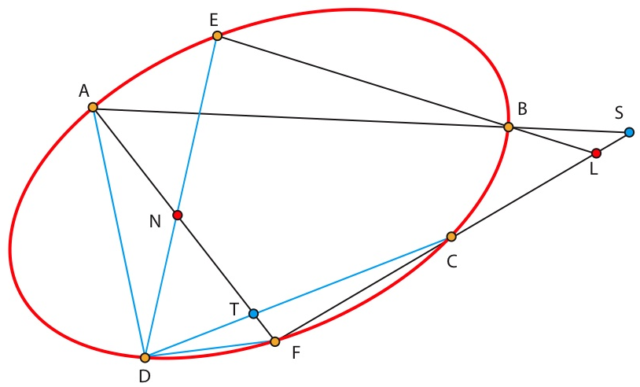
Es la última reunión de la Academia durante el gobierno de la Comuna, antes de la Semana Sangrienta (21 a 28 de mayo). Desaparecen las líneas entre (B) y (C) y entre (B) y (F), y las que el 8 de mayo estaban en rojo, cambian de color.
La narradora da el listado de los pocos asistentes a la reunión, entre ellos Antoine-Joseph Yvon Villarceau, conocido por una famosa construcción relacionada con el toro.
—oOo—
22 DE MAYO
SEA K=(LN)∩(AB).
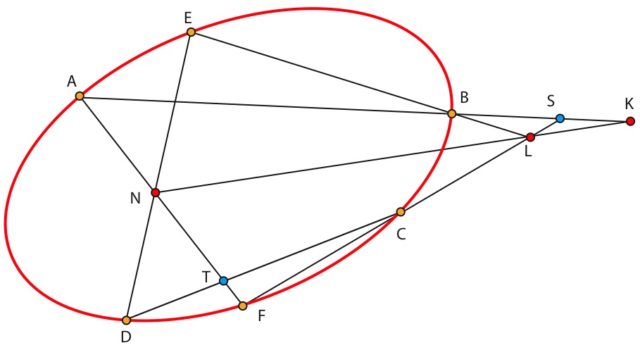
Aparece de nuevo a Sofía Kovalevskaya (K), que ya no está en París. Está relacionada con Newcomb (N) –ambos leen a Laplace– y con Lissagaray (L) –ella fue una de las mujeres de la Comuna–. Sofia fue también colega de Hermite (H) y de Bertrand (B), ya que tras su tesis, todo su trabajo y la demostración del teorema de Cauchy-Kovalevskaya, adquirió el estatus de matemática profesional.
—oOo—
29 DE MAYO
LA PERSPECTIVA DE CENTRO K QUE ENVÍA CF SOBRE AF ENVÍA S SOBRE A, L SOBRE N Y F SOBRE F. LA IMAGEN DE C ES ENTONCES T.
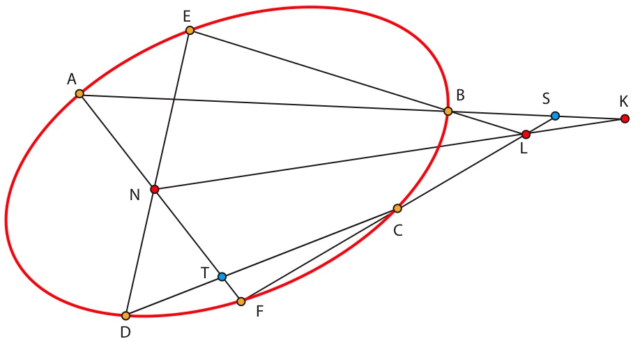
Como el lunes anterior, no hay reunión en la Academia. Todo ha terminado para la Comuna en París.
—oOo—
5 DE JUNIO
ASÍ K ∈ CT, ES DECIR CD. POR LO TANTO K=M.
Tiene lugar una reunión en la Academia, en la que se habla poco de ciencia y más de la masacre cometida en París. Y se ve que (K)=(M), es decir, la narradora ha sido Sofía Kovalevskaya… el teorema-homenaje está demostrado, homenaje a las mujeres de la Comuna,… como Sofía. CQD
AGRADECIMIENTO: Quería agradecer a Michèle Audin –además de esta maravilla de texto– el haberme permitido utilizar las imágenes que acompañan a Mai Quai Conti.
Notas:
i El título es un lipograma: no se emplea la letra ‘e’, como en La Disparition de Georges Perec.
ii La Comuna de París –La Commune de Paris– fue un movimiento insurreccional que gobernó esta ciudad entre el 18 de marzo y el 28 de mayo de 1871, instaurando un proyecto político popular autogestionario. Regentó París durante 60 días promulgando, una serie de decretos revolucionarios –como la autogestión de las fábricas abandonadas por sus dueños, la creación de guarderías para los hijos de las obreras, la laicidad del Estado, la remisión de los alquileres impagados o la abolición de los intereses de las deudas–, que en su mayoría respondían a la necesidad de paliar la pobreza generalizada que había causado la guerra. La Comuna fue reprimida con extrema dureza: tras un mes de combates, el asalto final al casco urbano provocó una dura lucha en la calle–la denominada Semana Sangrienta, Semaine sanglante– del 21 al 28 de mayo; el balance final fue de unos 30.000 muertos y el sometimiento de París a la ley marcial durante cinco años. La Comuna pedía:
El reconocimiento y la consolidación de la República como única forma de gobierno compatible con los derechos del pueblo y con el libre y constante desarrollo de la sociedad. La autonomía absoluta de la Comuna, que ha de ser válida para todas las localidades de Francia y que garantice a cada municipio la inviolabilidad de sus derechos, así como a todos los franceses el pleno ejercicio de sus facultades y capacidades como seres humanos, ciudadanos y trabajadores. La autonomía de la Comuna no tendrá más límites que el derecho de autonomía igual para todas las demás comunas adheridas al pacto, cuya alianza garantizará la Unidad francesa.
Declaración de la Comuna de París al Pueblo Francés, 19 de abril de 1871
iii La Academia de Ciencias de Francia –l’Académie des sciences– es la institución que: Anima y protege el espíritu de la investigación, y contribuye al progreso de las ciencias y de sus aplicaciones. Creada en 1666, durante el reinado de Luis XIV, contó inicialmente con científicos como René Descartes, Blaise Pascal y Pierre de Fermat.
v Os recomiendo que entréis a verlo en http://blogs.oulipo.net/ma/: el texto va acompañado de una extensa colección de documentos gráficos.
vi El teorema de Pascal –o Hexagrammum Mysticum Theorem– es un teorema de geometría proyectiva que generaliza el Teorema del hexágono de Pappus y es el dual proyectivo del Teorema de Brianchon. Fue descubierto por Blaise Pascal en 1639, cuando tenía tan solo dieciséis años.
vii Para las nociones de geometría proyectiva que aparecen, se puede consultar, por ejemplo, el libro Geometríade Carlos Ivorra Castillo, disponible gratuitamente en pdf.
viii Dados cuatro puntos distintos A, B, C y D sobre una recta, su razón doble o anarmónica [A,B,C,D] es el cociente de AC . DB entre AD . CB.
La razón doble o anarmónica de cuatro rectas concurrentes OA, OB, OC, OD es [OA,OB,OC,OD], el cociente de sen(AOC) . sen(DOB) entre sen(AOD) . sen(COB).
Se puede probar que: La razón doble de un haz de cuatro rectas es igual a la razón doble de cuatro puntos alineados en los cuales cualquier transversal que no pase por el vértice corta las cuatro líneas.
Además, si O y P son puntos sobre una cónica, [OA,OB,OC,OD]= [PA,PB,PC,PD].
ix ¿Quién soy yo? ¿Quién soy para poder contar esta historia? Hablar al mismo tiempo, casi con una misma frase, de Prosper-Olivier Lissagaray y de Simon Newcomb?
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.