El monte Jaizkibel se alza sobre las ciudades de Fuenterrabía, Irún, Pasajes, Rentería y Lezo (Guipúzcoa, País Vasco). Posee unos afloramientos rocosos –áreas en las que el terreno está formado por capas de rocas sin vegetación– en su parte más oriental, zona conocida como Formación Jaizkibel (edad Eoceno).
En la serie de artículos [1] a [3], el equipo de Carlos Galán del Laboratorio de Bioespeleología de la Sociedad de Ciencias Aranzadi estudia ciertas geoformas situadas sobre un conjunto de escarpes de arenisca en la Formación Jaizkibel. Esas geoformas incluyen –según se enumera en [3]– boxworks, cintas perforadas, bandas de Moebius, formas residuales de disolución, estructuras de corriente, nódulos, láminas e inclusiones ferruginosas, figuras de intercepción y anillos de Liesegang.
Aunque mis conocimientos de geología son nulos, cuando un compañero geólogo me comentó la inclusión de bandas de Moebius en la descripción de la Formación Jaizkibel, me animé a buscar estas superficies en los artículos de Carlos Galán y su equipo.
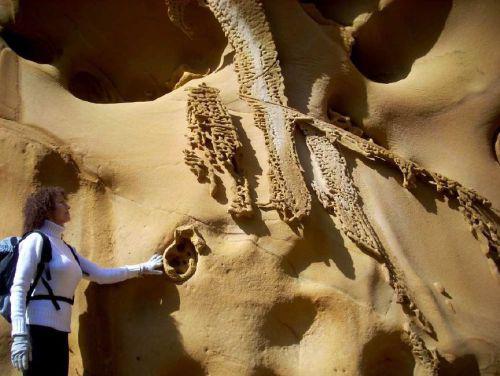
En [2], los autores describen las geoformas que denominan ‘bandas de Moebius’ del siguiente modo:
La formación de patrones en forma de cintas o bandas adquiere su más extravagante expresión en las geoformas que hemos denominado informalmente “bandas de Moebius”. Estas se encuentran en paredes de abrigos y cuevas en avanzado estado de arenización. Forman bandas delgadas que destacan de la roca en relieve positivo con un perfil en T: el trazo superior de la T forma una banda separada paralela a la superficie de la pared y el trazo vertical sirve de unión entre la banda y la pared de roca. La banda en sí está perforada por alveolos, sobre todo en sus bordes externos, que resultan recortados por muescas. Las bandas de este tipo pueden tener desarrollos sinuosos, de varios metros, siguiendo la curvatura de las paredes de las cavidades, por lo que en ocasiones recuerdan el desarrollo sin fin de la figura matemática llamada banda de Moebius. Aunque predominan las bandas verticales o que siguen la línea de mayor pendiente, las hay oblicuas y entrelazadas.

Tras la descripción de estas geoformas, los autores incluyen un párrafo en el que citan algunas características de la banda de Möbius: es una superficie no orientable, sólo posee una cara, tiene un único borde y es una superficie reglada. Explican también como puede construirse pegando dos lados opuestos de una cinta de papel tras un giro de 180 grados; incluso comentan qué sucede si se corta una banda de Möbius longitudinalmente:
Si se corta una cinta de Moebius a lo largo, a diferencia de una cinta normal, no se obtienen dos bandas, sino una banda más larga pero con dos vueltas. Si a ésta banda se la vuelve a cortar a lo largo, se obtienen otras dos bandas entrelazadas pero con vueltas. A medida que se va cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.
Recordemos que la anterior propiedad es solo cierta si se corta la banda de Möbius longitudinalmente por la altura mitad. En la anterior descripción, esa banda más larga obtenida con dos vueltas es (homeomorfa a) un cilindro –lo que llaman una “cinta normal”–, por ello, al volver a cortarlo por la mitad longitudinalmente, se obtienen dos cilindros, pero enlazados. Al repetir la operación se van duplicando los cilindros, que se entrelazan por parejas y entre ellos.
En este párrafo, los autores también comentan que la banda de Möbius ha servido de inspiración en el mundo del arte, nombrando la película argentina Moebius basada en el cuento Un metropolitano llamado Moebius del astrónomo y escritor Armin Joseph Deutsch.
La descripción de esta serie de propiedades de la banda de Möbius, es un modo de justificar la elección del nombre de estas geoformas, al finalizar esta parte del artículo con esta afirmación:
Aspectos y caracteres paradójicos análogos los presentan las geoformas halladas en Jaizkibel
La metáfora de la banda de Möbius –aunque estas formaciones no lo sean en realidad– es una deliciosa manera de hablar de estas geoformas que, sin lugar a dudas, son bellas, singulares y sorprendentes… como una banda de Möbius.
Más información
[1] Carlos Galán y Marian Nieto, Bandas de Moebius, Boxworks y otras raras Geoformas en arenisca de la Formación Jaizkibel, Sociedad de Ciencias Aranzadi, 2010
[2] Carlos Galán y Marian Nieto, Bandas de Moebius, Boxworks y otras raras Geoformas en arenisca de la Formación Jaizkibel, Boletín Sedeck (Sociedad Española de Espeleología y Ciencias del Karst) 8, 20-41, 2012
[3] Carlos Galán, José Manuel Rivas, Robert Ionescu y Marian Nieto, Disolución intergranular y evolución de cuevas y geoformas: los ejemplos más extravagantes del mundo en erenisca de edad eoceno (Formación Jaizkibel, País Vasco), Sociedad de Ciencias Aranzadi, 2013
[4] Marta Macho Stadler, Las bandas de Möbius de Jaizkibel, ZTFNews.org, 11 marzo 2014
Nota: Muchas gracias a Carlos Galán por permitir utilizar las imágenes incluidas en sus artículos.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
La Formación Jaizkibel y sus singulares geoformas “de Möbius” | Infogeología
[…] un párrafo en el que citan algunas características de la banda de Möbius: es una superficie no orientable, sólo posee una cara, tiene un único borde y es una superficie reglada. Explican también como […]