Número áureo, divina proporción, razón dorada… son términos inevitablemente vinculados a las proporciones en el mundo artístico. Todos ellos (representados por la letra φ (phi)) se asocian al número irracional (un número de infinitos decimales) que se expresa mediante la siguiente ecuación:

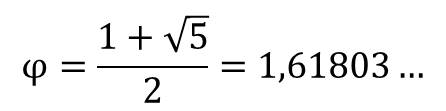
Pero tampoco es que este número nos diga mucho, así que vayamos con la interpretación geométrica, que resulta mucho más visual:

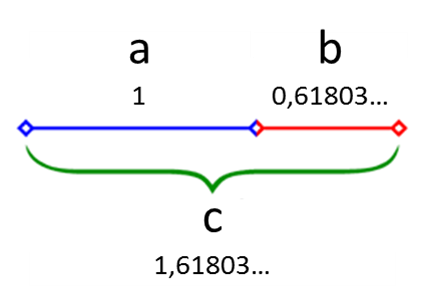
Se cumple la divina proporción cuando, al dividir un segmento (c) en dos partes (a y b), la relación entre el segmento original (c) y la parte más larga (a) es la misma que entre la parte más larga (a) y la más corta (b). Dicho de otro modo, cuando:

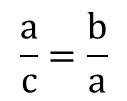
A estas proporciones se les atribuye un valor estético por lo que han sido aplicadas en obras artísticas de todo tipo: desde cuadros renacentistas hasta el diseño de logotipos* (Imagen 2).

Así que a nadie le sorprenderá que haya un software para trabajar con estas dimensiones o una página web exclusivamente dedicada al número áureo. Pero qué queréis que os diga, la cosa se nos ha ido un poco de las manos. Parece que ahora toda composición artística que se precie se adapta a la divina proporción o a la espiral áurea (la que se consigue mediante la combinación de rectángulos áureos). Hay una anécdota que refleja ese hecho a las mil maravillas. Nada más empezar 2016 un periodista comentó en twitter una peculiar fotografía que había dejado la celebración de la entrada en el nuevo año: “Suceden tantas cosas en esa imagen. Como en una hermosa pintura”. Enseguida el mensaje se hizo viral y comenzaron las parodias sobre la fotografía en cuestión. Entre ellas no podía faltar una referente a la espiral áurea.

Aunque, hablando de parodias sobre el número de oro, la que más me ha llamado la atención por lo bien que se adapta a la espiral áurea es la realizada sobre la cabeza del todopoderoso presidente de los Estados Unidos. Dejo en vuestras manos decidir si en este caso la composición es artísticamente deseable.

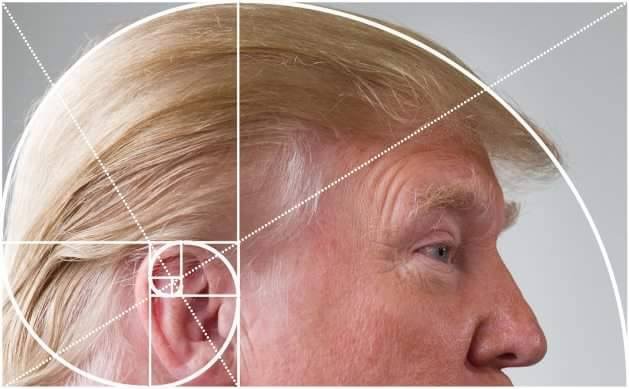
Pero este artículo no trata sobre el número áureo, del que ya se ha hablado mucho (aquí o aquí) desde que Euclides lo mencionase por primera vez en el s. III a.e.c. Aunque se supone que ya se empleó con anterioridad en la composición del Partenón (s. V a.e.c.) o, incluso, en las pirámides de Guiza (s. XXVI a.e.c.). Y precisamente hoy vamos a viajar a la tierra de las pirámides para conocer un sistema de proporciones más antiguo y mucho más “racional”. Lo haremos de la mano de un personaje que, pese a no haber trascendido al gran público, ocupa un puesto de honor en la historia del arte egipcio: el escriba real Hesiré.

Nos remontamos a la III dinastía del Egipto faraónico, allá por el 2650 a.e.c. cuando las famosas pirámides que acabamos de mencionar ni siquiera se habían empezado a construir. Muy cerca de donde unos años después se erigirían, en la necrópolis real de Saqqara, ya había sucedido un hito: se había establecido el canon egipcio. En mayor o menor medida todos estamos familiarizados con dicho canon. ¿Quién no ha visto alguna vez una imagen del estilo de la que os muestro a continuación?

La gran mayoría de las imágenes del Antiguo Egipto siguen unos principios compositivos idénticos. Por una parte, obedecen a lo que se conoce como principio de frontalidad: la cabeza y las extremidades se representan de perfil mientras que el torso aparece de frente. Si los pensáis, dicha posición es anatómicamente imposible a menos que fuesen expertos contorsionistas. Pero eso no era mayor problema, ya que se trata de una representación simbólica, muy alejada, por ejemplo, de las esculturas griegas que intentan reflejar la anatomía humana. Por otra parte, y la que más nos interesa en este artículo, todas estas figuras siguen un canon de proporciones basado en la aplicación matemática.

Estos principios compositivos perdurarían durante dos milenios en el arte egipcio sin apenas alteraciones. Casi nada. Pero, ¿cómo fue eso posible? Para entenderlo debemos abstraernos de nuestro concepto de arte. El arte egipcio estaba completamente supeditado a la experiencia religiosa y su misión era reflejar la inalterabilidad del orden divino. De hecho, ni siquiera existía el concepto de artista. Se trataba de un arte colectivo en el que cada artesano tenía una función (esculpir o pintar, por ejemplo). Tampoco existía el concepto de belleza que podemos tener hoy en día; ésta estaba asociada a la pericia en ejecutar las normas establecidas. De ahí que el canon se perpetuase de generación en generación con algunas excepciones como los convulsos periodos intermedios o el periodo Amarnense (durante el cual el faraón Akhenatón quiso establecer un sistema monoteísta; así que ya vemos que el arte seguía relacionado con el ámbito religioso). La creación del canon egipcio fue posiblemente un proceso paulatino que se asentó, como decíamos antes, en la III dinastía. Y ahí es donde entra en escena Hesiré o, mejor dicho, Hesiré y sus puños.

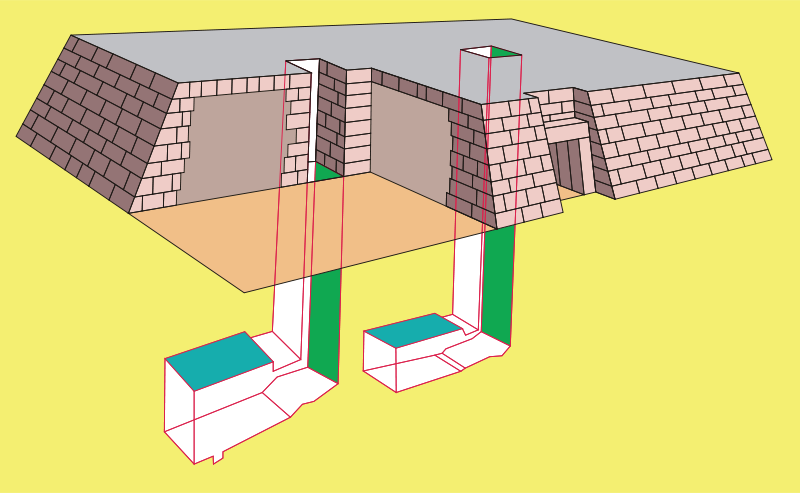
Allá por 1861 el arqueólogo Auguste Mariette estaba explorando la mastaba (tipo de enterramiento precursor de las pirámides) de dicho alto cargo del faraón en la necrópolis de Saqqara. Ante sus ojos apareció una fabulosa galería llena de pinturas y unos relieves que pasarían a la historia. Trabajados en madera de cedro de color rojizo, seis de ellos han sobrevivido hasta nuestros días en buenas condiciones pese a tratarse de un material perecedero. Alguna ventaja tenía que tener permanecer enterrado en el desierto.

Los relieves muestran al escriba real (uno de los tantos cargos que ostentaba) en diferentes etapas de su vida. En el que os muestro en la Imagen 7 aparece con una peluca corta antes una mesa de ofrendas mientras sujeta con la mano izquierda un bastón y sus útiles de escriba. En otros casos porta el Kherep (Imagen 8), un distintivo de poder que vuelve a resaltar la importancia del simbolismo en el arte egipcio. Pues bien, serán estos bajorrelieves los que nos ayuden a comprender el sistema de proporciones del arte egipcio.

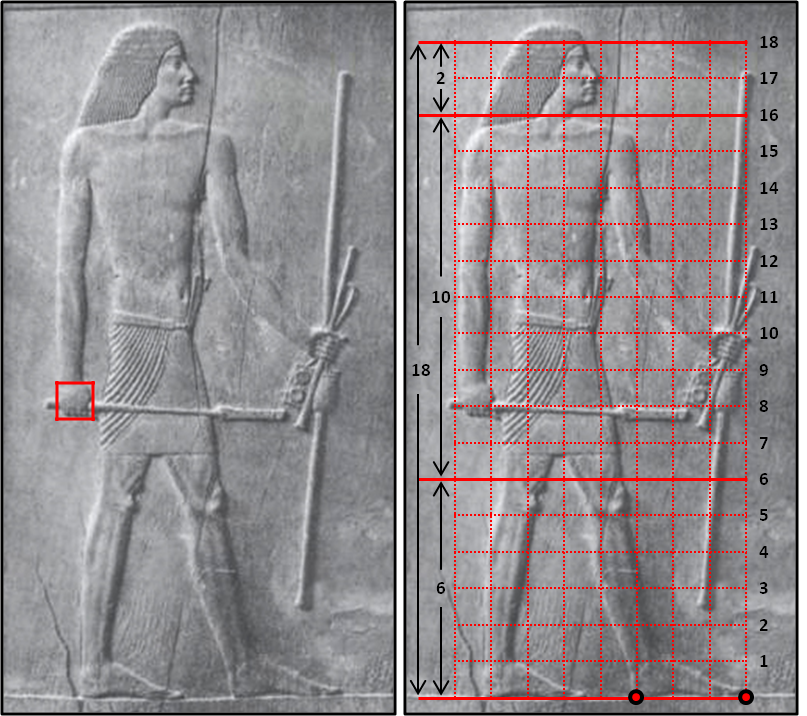
Los egipcios usaban un sistema de cuadriculas en el que cada parte del cuerpo ocupaba un número diferente de cuadrados. Antes os decía que los puños tendrían una gran importancia en esta historia y es que cada cuadrado era del tamaño de un puño^*. Partiendo de esa base, cada figura de pie tendría una altura de 18 cuadrados desde los pies hasta el nacimiento del pelo. Alguien podría pensar que lo lógico hubiese sido cubrir toda la altura de la figura, pero en el caso de que portase algún objeto en la cabeza las medidas resultarían más complicadas (¡lo tenían todo pensado estos egipcios!). Siguiendo con la misma referencia, las rodillas acabarían con el sexto cuadrado y el resto del cuerpo ocuparía 10 unidades, dejando las últimas dos para cubrir el cuello y la cabeza. En la Imagen 8 podéis ver cómo se cumplen esas propiedades en uno de los relieves. Si os fijáis, la cuadricula sirve para localizar y dar tamaño a diferentes partes del cuerpo: el ombligo está a la altura del undécimo cuadrado, los pies de Hesiré ocupan tres espacios, etc. Pues bien, este sistema permitía a los egipcios mantener un sistema de proporciones constantes en una composición por muchos personajes que apareciesen (a no ser que el simbolismo exigiese un cambio, como cuando el faraón se representaba de mayor tamaño para dejar constancia de su poder).

Tras ver la imagen anterior podemos comprender por qué las composiciones egipcias resultan tan “cuadriculadas”. Pero, ¿qué sucede cuando el personaje no está de pie? La verdad es que el sistema se aplica de una manera muy similar en las figuras sedantes, sólo que, obviamente, la altura es menor: 14 cuadrados. En todo caso, el único módulo que sufre cambios es el que va desde los hombros a las rodillas, que pasa a estar compuesto por seis cuadrados. Esto resulta lógico si tenemos en cuenta que es la parte del cuerpo que se dobla con el cambio de posición. Así, en la Imagen 9 podéis observar como el Hesiré que os mostraba ante la mesa de ofrendas cumple rigurosamente esta norma. Esto no supone ningún cambio en el resto de proporciones anatómicas, ya que el tamaño absoluto de la figura no varía, simplemente hay cuatro cuadrados que ocupan un espacio horizontal en lugar de vertical.

En este sistema, sencillo a la par que elegante, los egipcios encontraron el modo para perpetuar su canon artístico durante siglos, en un periodo que se prolongó entre las dinastías III (s. XXVII a.e.c) y la dinastía XXVI (s. VII a.e.c) donde las figuras se estilizaron y su altura superó los veinte cuadrados. Así, aunque Hesiré no haya logrado la fama de sus paisanos Nefertiti o Tutankamón, su nombre ocupa un puesto de honor en la historia del arte egipcio.

Notas:

(1): Como pudimos ver hace unos días en el curso M de Matemáticas que organizan cada verano Marta Macho y Raúl Ibáñez (fieles colaboradores del Cuaderno en la sección Matemoción), y a los que pido disculpas por el intrusismo de esta entrada.

(2): El sistema de puños propuesto por el egiptólogo Erik Iversen fue replanteado por Gay Robins y más recientemente por John Legon. Según este último autor la cuadricula en la que se basa el canon de proporciones surgiría de dividir el cuerpo en tres partes iguales (6 cuadrados) de las que luego se realizarían otras subdivisiones. En cualquier caso, dado que el objetivo de este artículo es dar a conocer que el arte egipcio empleaba un sistema de proporciones basado en una cuadricula, se ha decidido mantener el concepto de puño.

Para saber más:

Gay Robins “Proportion and Style in Ancient Egyptian Art” University of Texas Press (1993).

Joan Kee “To Scale” Wiley-Blackwell (2016).

Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.