
Normalmente cuando hablamos de la relación entre el Arte y las Matemáticas acudimos a ejemplos de obras de algunos de los grandes artistas de la Historia del Arte (Leonardo, Durero, Velázquez, Gaudí, Picasso, Mondrian, Dalí, Pollock, etc), con el objetivo de poner de manifiesto la importancia y el interés de dicha relación. Sin embargo, lo habitual es que conozcamos esas esculturas, pinturas y demás manifestaciones artísticas a través de fotografías en libros, en internet o a través de la televisión, pero no en persona, que es como realmente se aprecian.
Aunque si se quiere llamar la atención del público sobre el nexo entre Arte y Matemáticas, seguramente la opción más apropiada sea la anterior. Sin embargo, yo soy partidario de mirar también a nuestro entorno más cercano, de entrar en los museos, y galerías de arte, que están en nuestras ciudades y buscar en ellos ejemplos de dicha conexión. Obras de arte que podemos admirar directamente, y de artistas, en muchos casos, de nuestra región. Por este motivo, cuando mi amigo César Ochoa, del Museo de Bellas Artes de Bilbao, me invitó hace algunos años a dar un par de charlas sobre Arte y Matemáticas, los dos lo tuvimos claro, había que mirar al interior del museo y buscar allí esos ejemplos.

Lo primero que hicimos fue dar un paseo los dos juntos, Cesar y yo, por las obras que se estaban exponiendo en ese momento en el museo. Yo buscaba ejemplos de pinturas y esculturas relacionadas con los temas matemáticos que personalmente me eran más interesantes y afines, como por ejemplo, la abstracción, las figuras geométricas planas, los poliedros, las curvas y las superficies, las proyecciones geométricas, las ilusiones ópticas, las simetrías, los números o el infinito. Y encontramos ejemplos muy interesantes, aunque en esta entrada no vamos a entrar en ellos. Sin embargo, en un principio no me interesé mucho por la proporción áurea, y otras proporciones, puesto que es un tema que ha sido demasiado tratado, incluso en exceso.
Sin embargo, mientras paseábamos llegamos a la obra “Pescadores vascos” (1918) del pintor bilbaíno Alberto Arrúe Valle (1878-1944), cuya estructura en dos partes me hizo pensar en el formato DIN A de las hojas de papel, y empecé a pensar que quizás sería interesante incluir algunos ejemplos de proporciones en mis charlas.
Pero expliquemos cuál es la proporción de las hojas de papel DIN A. Para empezar, si tenemos dos segmentos de longitudes a y b, en particular, las dimensiones de un rectángulo, la proporción entre ellos es b/a (o también, a/b).
La proporción asociada a un rectángulo es un “concepto matemático” que recoge información sobre la forma de este. Dos rectángulos que tengan la misma proporción entre sus lados tendrán la misma forma, simplemente que uno será una ampliación o una reducción del otro.

En el caso de las hojas de papel de formato DIN A, hay dos propiedades que van a determinar sus dimensiones, y en particular, su proporción.
A. Están adaptadas a ampliaciones y reducciones. La proporción de los diferentes tamaños de las hojas de papel DIN A (desde el DIN A0 al DIN A10) es siempre la misma, lo que facilita la ampliación y la reducción a la hora de realizar fotocopias, puesto que todas tienen la misma forma. El uso simultáneo de formatos con distintas proporciones dificultaría las labores de fotocopiado e impresión, puesto que al ampliar o reducir quedarían zonas sin fotocopiar o aparecerían espacios “negros”.
B. Es fácil pasar de un tamaño a otro. Se pasa de un tamaño al siguiente uniendo dos copias del primero, o al anterior, partiéndolo por la mitad. Así, uniendo dos DIN A4 obtenemos un DIN A3, y juntando dos DIN A3 se forma un DIN A2, sin embargo, si partimos una hoja DIN A4 por la mitad se consiguen dos hojas DIN A5.
Estas dos propiedades determinan cual es la proporción que tienen las hojas de papel con formato DINA.
Si juntamos dos hojas de papel de dimensiones a (ancho) y b (alto), como aparece en la imagen, se obtiene un nuevo rectángulo de dimensiones b y 2a (propiedad B). Como ambas deben de tener la misma proporción (propiedad A), entonces
Por lo tanto, , luego el cuadrado de la proporción es 2,
. Es decir, la proporción del formato DIN A es
.
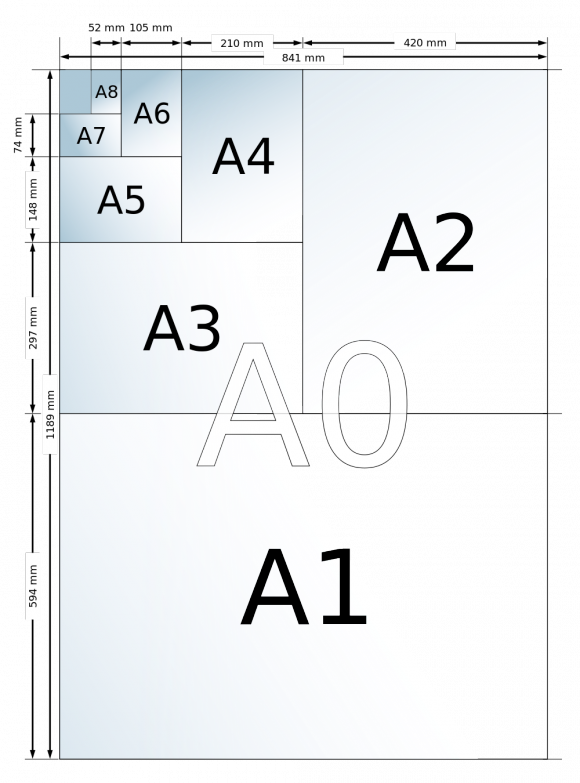
Las medidas exactas de cada uno de los tamaños vienen determinadas por el hecho de que el papel de tamaño DIN A0 mide exactamente 1 m2, o lo que es lo mismo 10.000 cm2. De donde, las medidas del tamaño DIN A0 son 84,1 cm y 118,9 cm. Por lo tanto, si consideramos el tamaño más común, el DIN A4, como su superficie es igual a 10.000/16=625 cm2, por la propiedad B, y como la proporción es raíz de dos, tenemos que sus medidas son 21,022 cm y 29,729 cm.
Problema: ¿Cuál es la ampliación que hay que hacer para transformar una imagen de una hoja DIN A4 a una de DIN A3?
En el cuadro “Pescadores vascos” puede observarse que está dividido en dos zonas, más o menos rectangulares, en las que están el “arrantzle” (pescador) y su mujer, claramente diferenciadas por el remo que sujeta el pescador en su mano. Al ver el cuadro me dio la impresión de que ambas zonas rectangulares podían tener la misma proporción que todo el cuadro. Y así fue. Si tomamos las medidas que aparecen en el Museo de Bellas Artes este cuadro tiene unas dimensiones aproximadamente de 135,5 cm de alto y 190,5 cm de ancho, cuya proporción es casi raíz de dos, 1,41. Y como puede apreciarse en la siguiente imagen el cuadro está dividido en dos rectángulos de proporciones también .

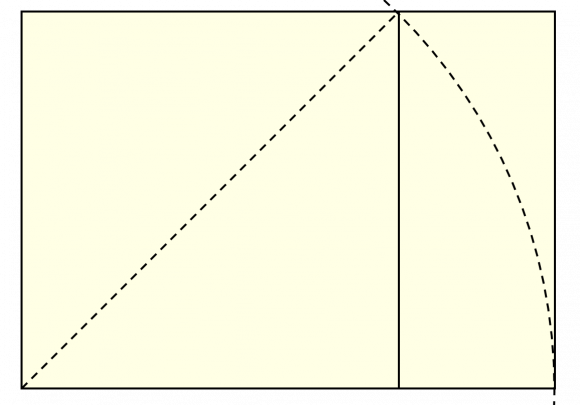
Hay varias formas de construir geométricamente un rectángulo con proporción . La más sencilla es partir de un cuadrado, podemos suponer que su lado es de longitud 1, por lo tanto su diagonal medirá (haciendo uso del Teorema de Pitágoras)
, y pintar un arco de circunferencia de radio la diagonal, con lo que se marca el lugar hasta donde habrá que extender uno de los lados del cuadrado para obtener el rectángulo deseado, como se ve en la imagen.
Curiosamente, esta división de un rectángulo raíz de dos en una zona cuadrada y el complemento rectangular pude observarlo en una de las deliciosas obras del pintor madrileño, nacido en Lisboa, Ricardo Balaca y Orejas Canseco (1844-1880), “Estudiantina” (1864).


No sé si Alberto Arrúe y Ricardo Balaca eran conscientes de que el “lienzo” sobre el que pintaron ambos cuadros tenía la proporción , lo que parece más claro es que en ambas obras los autores pudieron llegar a este rectángulo a través de sus propiedades geométricas. Además, personalmente creo que esta proporción nos ayuda a explicar la estructura de cada una de las obras.
Llegados a este punto me puse a jugar un poco y busqué algunas otras obras que pudieran tener proporción . Entre ellas encontré “Represión” (1975) del pintor vizcaíno Dionisio Blanco Ortega (1927-2003), cuyas proporciones eran cercanas a la raíz de dos. Pero lo que llamó mi atención de esta obra es que cuando puse encima la estructura del cuadrado más el arco de circunferencia, que hemos mostrado más arriba, tanto por la derecha como por la izquierda, el lienzo se dividía en una serie de zonas significativas. Los policías, de gris, y los detenidos, de colores, en los que se centraba la atención del pintor, y por tanto, de quien observa la obra, estaban situados en la zona central, bajo las dos diagonales de los cuadrados. Mientras que había más policías y manifestantes alejados de la escena central, que estaban pintados en las dos zonas exteriores de los arcos de circunferencia. Esas eran zonas rosas, y en una de las partes al menos, se seguía claramente el arco de circunferencia.

En el caso de esta pintura de Dionisio Blanco, el nexo de la misma con la proporción raíz de dos es puramente subjetiva, fruto del juego realizado con algunas de las obras del museo. No hay ninguna evidencia de que fuese utilizada conscientemente, pero es interesante observar cómo nos ayuda, al menos a mí, a entender la estructura el cuadro.
Entonces me planteé si podría haber alguna otra obra que estuviera relacionada con alguna otra proporción dinámica de la forma . Me planteé si habría algún tríptico, o alguna obra en tres partes, tal que la proporción del total fuese igual a la proporción de cada una de las tres partes. Y descubrí que ese era el caso de “Gólgota” (1964), del pintor madrileño Lucio Muñoz Martínez (1929-1998). Una obra que por lo tanto tiene la proporción
.

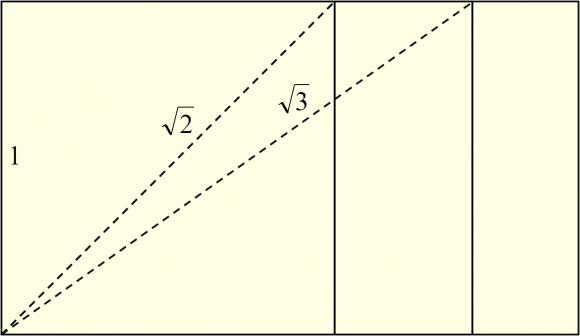
Por cierto, que la proporción raíz de tres aparece asociada a la Vésica Piscis, puesto que la relación entre su altura y anchura es precisamente este número. O de forma equivalente, el rectángulo que circunscribe a la Vésica Piscis tiene dicha proporción.
Una vez metido en el tema de las proporciones, no podía dejar de fijar mi atención en la proporción más famosa, la proporción áurea. Existe bastante literatura sobre la utilización de la divina proporción, y otras proporciones, en el arte, la arquitectura o el diseño (algunas referencias se muestran en la bibliografía). Respecto al tema que estamos tratando en esta entrada, el libro “Tramas, la geometría secreta de los pintores”, de Charles Bouleau, analiza la utilización de diferentes proporciones, en particular, la razón áurea, para el diseño de la estructura de los cuadrados, lo que el autor llama “la trama de la pintura”, debido al entramado de líneas rectas de la estructura.
Aunque parece ser que la proporción áurea fue estudiada por los pitagóricos, la primera definición aparece en el gran libro “Los Elementos” de Euclides (aprox. 325-265 a.c.). Y dice así: “Se dice que un segmento está dividido en media y extrema razón cuando la longitud del segmento total es a la parte mayor, como la de esta parte mayor es a la menor”.
Si suponemos que la parte mayor del segmento tiene longitud 1 y el segmento x, entonces la parte menor es x-1, de donde la condición para determinar el punto del segmento que lo divide en media y extrema razón es
y operando nos queda la ecuación de segundo grado . Cuya solución positiva, haciendo uso de la fórmula para resolver ecuaciones de segundo grado, es igual a
Esta sencilla razón es la que posteriormente acabaría llamándose número de oro, razón aurea o divina proporción, y que se suele denotar por la letra griega phi, .
Un rectángulo, en particular, el lienzo de un cuadro, se dice que es un rectángulo áureo si la proporción entre su ancho, p, y su alto, q, es precisamente la razón áurea,
.
Los rectángulos áureos tienen curiosas propiedades, como la que aparece en la siguiente imagen, aunque el estudio de las propiedades del número de oro no es el objetivo de este artículo del Cuadernode Cultura Científica.
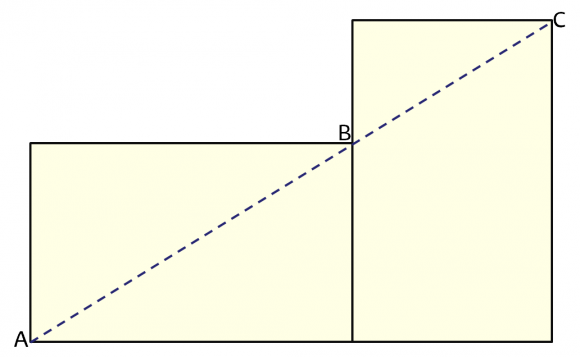
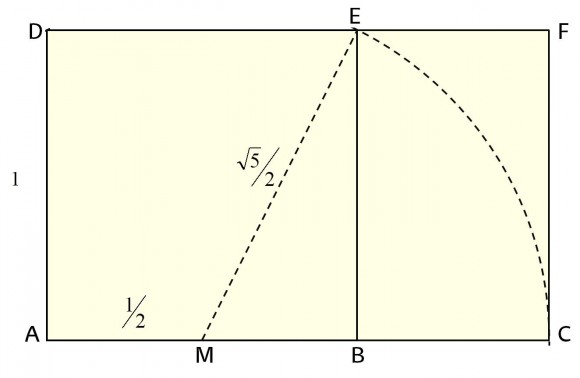
Al igual que en el caso del rectángulo con la proporción raíz de dos, ahora también existen sencillas construcciones geométricas del rectángulo áureo. Si partimos de un cuadrado, que podemos suponer que tiene los lados de longitud 1, y tomamos el punto medio de uno de sus lados, en la imagen el punto M que es el punto medio del segmento AB, entonces el segmento que une el punto medio M con uno de los vértices opuestos del cuadrado, F en la imagen, y que tiene longitud igual a $sqrt{5}/2 $,nos sirve de radio para trazar un arco de circunferencia que nos determinará el lado largo del rectángulo áureo. Se extiende el segmento AB hasta el punto C, que es la intersección del arco de circunferencia y la extensión del lado AB. Por lo tanto, tenemos un rectángulo de altura 1 y anchura igual a , luego de proporción áurea. Además, el rectángulo que hemos añadido también tiene proporción igual al número de oro, puesto que sus dimensiones son 1 y
, esta última igualdad se debe a que
es solución de la ecuación anterior,
.
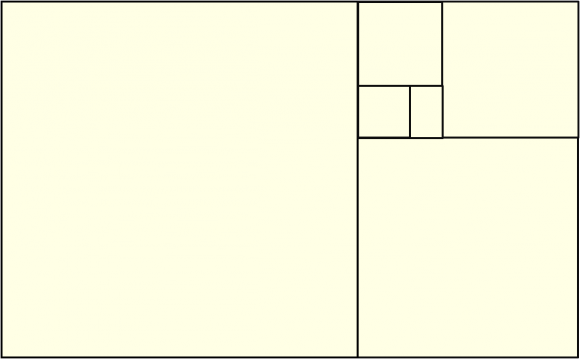
Al revés, cualquier rectángulo áureo puede descomponerse en un cuadrado y un rectángulo áureo más pequeño. Y si continuamos esta descomposición, con este nuevo rectángulo áureo, se construye un entramado de cuadrados y rectángulos áureos dentro del rectángulo inicial, como se muestra en la imagen.
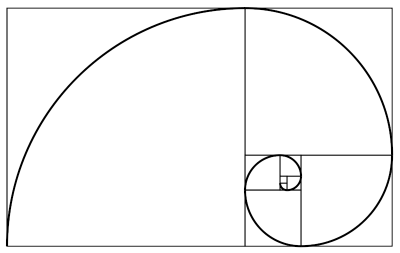
A partir de esta descomposición se construye la espiral de Durero como unión de arcos de circunferencias (véase la siguiente imagen).

Llegados a este punto busqué cuadros del Museo de Bellas Artes de Bilbao que pudieran tener, aproximadamente, la divina proporción, y además “investigué” si algunas de las cuestiones relacionadas con la proporción de oro podían ayudarme a entender la estructura de la obra. Por supuesto, esto era una perspectiva puramente subjetiva, que quizás no tuviese nada que ver con las intenciones del autor, o sí, pero que a mí me ayudaban a entender su estructura, en un primer acercamiento a la obra (y digo “un primer acercamiento”, puesto que el entramado estructural de la obra suele ser de una cierta complejidad y no se adivina a simple vista).
Así, descubrí el cuadro “Después de la misa en la iglesia de Arteaga”, de pintor bilbaíno Anselmo Guinea Ugalde (1855-1906). El cuadro está dividido en dos escenas, una principal –un hombre, ¿el sacristán?, con la cruz procesional- y otra secundaria –las mujeres rezando-. Al considerar la descomposición del lienzo áureo en un cuadrado, más un pequeño rectángulo áureo, vemos que la escena principal está en el cuadrado y la secundaria en el pequeño rectángulo. Además, la diagonal del cuadrado nos marca una de las líneas principales de la obra, que es la dirección de la cruz procesional que sujeta el hombre.

El mismo juego se puede hacer con su cuadro “Recuerdos de Capri” (Anselmo Guinea, 1884).
Otra obra que me gusta mencionar, y que aunque su lienzo tiene la proporción de oro es muy probable que su autora no la utilizara en el sentido que yo voy a comentar, es la pintura “El Arenal al fondo” de la pintora bilbaína Mari Puri Herrero (1942-). De nuevo la escena del cuadro se puede dividir en dos, la principal, enmarcada dentro del cuadrado, más luminosa, con el ventanal en el medio y las dos mujeres mirando por el mismo. Y la parte rectangular, que es la escena secundaria, más oscura y en ella están colocados los hombres.

Para finalizar, un cuadro de una de las pintoras españolas más interesadas en la divina proporción, y estudiosa de la misma, como es la Maruja Mallo (1902-1995). Quien ha podido estudiar las tramas de las estructuras de sus cuadros ha podido ver su complejidad y el uso continuado de en las mismas. Pueden verse algunas de esas tramas (trazados armónicos), por ejemplo, en el libro “Maruja Mallo” de Estrella de Diego, o en algunos de los catálogos de sus exposiciones.

Esta obra merecería un análisis muy detallado, puesto que solo con una mirada inicial ya se intuye un complejo entramado áureo (la cabeza, las manos, etc). En particular, la altura del lienzo está dividida en dos partes en proporción áurea, marcado por el hierro horizontal.
Bibliografía
1.- Museo de Bellas Artes de Bilbao
2.- Fernando Corbalán, La proporción áurea, el lenguaje matemático de la belleza, RBA, 2010.
3.- Charles Bouleau, Tramas, la geometría secreta de los pintores, Arte y Estética 47, Akal, 1996.
4.- Carmen Bonell, La divina proporción, las formas geométricas, UPC, 1999.
5.- Matila Ghyka, Estética de las proporciones en la Naturaleza y en las Artes, Poseidón, 1977.
6.- Mario Livio, La proporción áurea, la historia de phi, el número más sorprendente del mundo, Ariel, 2006.
7.- Kimberly Elam, Geometry of Design, Princeton Architectural Press, 2001.
8.- M. Encarnación Reyes, Arte y Naturaleza en clave geométrica, Un paseo por la geometría, 2005/06, UPV-EHU, 2006.
9. Estrella de Diego, Maruja Mallo, Fundación MAFRE, Instituto de Cultura, 2008.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica



Visitad los museos, también en clave matemática
[…] Visitad los museos, también en clave matemática […]
Visitad los museos, también en clave mat…
[…] propPescadores vascos (1918), Alberto Arrúe, óleo sobre lienzo, 135,5 x 190,5 cm Normalmente cuando hablamos de la relación entre el Arte y las Matemáticas acudimos a ejemplos de obras de algunos de los grandes artistas de la Historia del Arte […]
Visitad los museos, también en clave mat…
[…] Pescadores vascos (1918), Alberto Arrúe, óleo sobre lienzo, 135,5 x 190,5 cm Normalmente cuando hablamos de la relación entre el Arte y las Matemáticas acudimos a ejemplos de obras de algunos de los grandes artistas de la Historia del Arte… […]
Visitad los museos, también en clave mat…
[…] Pescadores vascos (1918), Alberto Arrúe, óleo sobre lienzo, 135,5 x 190,5 cm Normalmente cuando hablamos de la relación entre el Arte y las Matemáticas acudimos a ejemplos de obras de algunos de los grandes artistas de la Historia del Arte […]
El hechizo matemático del arte. Cultura con M de Matemáticas | ACTIVA TU NEURONA
[…] https://culturacientifica.com/2014/04/09/visitad-los-museos-tambien-en-clave-matematica/ https://culturacientifica.com/2014/01/15/el-salto-de-la-rana-y-familia/ […]
Señales más allá del tiempo | Frontera | Cuaderno de Cultura Científica
[…] han reflexionado ya sobre el arte y su relación con otras ciencias. Raúl Ibáñez, nos proponía, visitar los museos también en clave matemática, y recientemente en un curso de verano de la Universidad del País Vasco, organizado por Marta […]
Seinaleak etorkizunekoentzat | Dibulgazioa | Zientzia Kaiera
[…] egin dute artearen eta zientzien arteko muga betean ibilita. Raúl Ibáñezek, proposatu zigun matematikaren ikuspegitik ere bisitatzea museoak, eta orain dela gutxi, Euskal Herriko Unibertsitateko uda-ikastaro batean, publikoak edertasunari […]
Arte y matemáticas | Matemerce
[…] Visitar museos en clave matemática […]
Los museos como herramienta de comunicación | Frontera | Cuaderno de Cultura Científica
[…] Visitad los museos, también clave matemática […]
Hesiré o las proporciones en el arte antes del número áureo – Cuaderno de Cultura Científica
[…] este artículo no trata sobre el número áureo, del que ya se ha hablado mucho (aquí o aquí) desde que Euclides lo mencionase por primera vez en el s. III a.e.c. Aunque se supone que […]
ECHO, un cómic áureo — Cuaderno de Cultura Científica
[…] de oro, del cual ya hemos hablado en el Cuaderno de Cultura Científica en algunas entradas como Visitad los museos, también en clave matemática, ¿Es áureo el Aston Martin de James Bond? ó Crímenes […]