En mi anterior entrada del Cuaderno de Cultura Científica, Muerte entre las ecuaciones (Historias de muerte y matemáticas 1) [], comentamos las curiosas muertes de algunos matemáticos, Pitágoras, Arquímedes, Hipatia, Eratóstenes, Cardano, de Moivre, Descartes y Euler. Como ya anunciaba el número “1” que acompañaba al subtítulo, mi intención era seguir en esta nueva entrada con más historias de muerte y matemáticas.
Teniendo en cuenta que el sábado que viene es el 471 aniversario de la muerte del astrónomo polaco Nicolás Copérnico(19 de febrero 1473-24 de mayo de 1543), empezaremos con una anécdota relacionada con su muerte.
Al parecer el padre de la teoría heliocéntrica del sistema solar escribió su obra maestra, De revolutionibus orbium coelestium (Sobre las revoluciones de las esferas celestes), hacia 1530 (tras unos 20 años trabajando en la misma), sin embargo, no la publica y al parecer tampoco tiene intenciones de hacerlo, por lo que quedó temporalmente guardada en un cajón. Si se llegó a publicar finalmente, en mayo de 1543, fue gracias a su alumno Georg Joachim Rhaeticus.

En 1539 Rhaeticus fue a estudiar con Copérnico, con quien estuvo dos años. Se convirtió en un entusiasta del sistema heliocentrista del sistema solar, y no solo fue el responsable de convencer a Copérnico de que finalmente publicara De revolutionibus orbium coelestium, sino que también lo fue de que su maestro pudiera ver impresa su obra antes de morir. Según cuenta Rhaeticus, en cuanto estuvo impresa la primera copia de la obra De revolutionibus orbium coelestium corrió a enseñársela a Copérnico, que estaba moribundo en su cama. A finales de 1542 había sufrido una hemorragia cerebral que lo incapacitó parcialmente y supuso un grave deterioro de su salud, hasta su muerte en mayo de 1543. Sin embargo, gracias a su alumno, el astrónomo pudo tocar y ver su libro impreso, justo antes de morir con la copia en sus manos…
En Historias de muerte y matemáticas 1, comentábamos que la muerte de Arquímedes era una de las más famosas y conocidas. Sin embargo, la muerte perteneciente al ámbito de las matemáticas que más ha llamado la atención y cautivado siempre, dentro y fuera de esta ciencia, ha sido la del joven matemático francés Évariste Galois (1811-1832). Este murió a la edad de 20 años como consecuencia de un duelo, pero a pesar de su corta edad, se convirtió en uno de los grandes matemáticos de todos los tiempos. A él le debemos el hallazgo de las condiciones necesarias y suficientes para que la ecuación polinómica general de grado n () fuese resuelta por medio de radicales, lo que le llevó a poder demostrar que para grados mayores que 4 la ecuación polinómica no podía resolverse por medio de radicales, contrariamente a lo que ocurría para los grados 2 (que es la fórmula que estudiamos en la enseñanza secundaria), 3 y 4. Su trabajo revolucionó el álgebra abstracta, una de cuyas ramas es hoy en día la Teoría de Galois.

Évariste Galois fue un joven inconformista y rebelde que dedicó su corta vida a la revolución y a las matemáticas. Su primer artículo lo publicó con 17 años en la revista Annales de matemátiques pures et appliquées, pero no vamos a hablar aquí de asuntos matemáticos como sus problemas para entrar en la Escuela Politécnica o con las memorias matemáticas que envió a la Academia de Ciencias.
Después de la revolución de 1830, Évariste entraría en la Sociedad de Amigos del Pueblo, una organización popular que intentaba cambiar la situación política y social de Francia, y que utilizaba métodos violentos para ello. A raíz de una carta supuestamente escrita por él en la Gazette des Écoles, sobre el director de la Escuela Normal y su actuación durante la revolución de 1830, sería expulsado de la Escuela Normal, con polémica pública incluida. Y poco después publicaría su conicida Carta sobre la enseñanza de las ciencias, poniendo en cuestión la enseñanza de las ciencias en su país, y que empieza así:
De entrada en las ciencias, las opiniones no cuentan para nada; los puestos no tendrían que ser la recompensa de una u otra manera de pensar en política o en religión. Me informo de si un profesor es bueno o malo, y me preocupa muy poco su forma de pensar en materias ajenas a sus estudios científicos…” (Gazette des Écoles, 2 de enero de 1831).
En ese tiempo los republicanos se echaron a la calle, que estaba muy agitada y era muy hostil con el gobierno. En un restaurante de París se celebró un homenaje en honor de un grupo de republicanos absueltos de los cargos de conspiración y al que acudieron unos doscientos radicales, entre los que estaban Galois, sus compañeros de la Sociedad de Amigos del Pueblo y Alejandro Dumas, el autor de Los tres mosqueteros, quien documentaría los hechos que allí acontecieron. Galois realizó un brindis amenazante, cuchillo en mano, contra el rey Luis Felipe, por lo que iría un mes a la cárcel, aunque sería finalmente absuelto.
Poco después, en el aniversario de la toma de la Bastilla, el 14 de julio de 1831, sería detenido por vestir el uniforme de la ilegal Guardia Nacional, y pasaría nueve meses en prisión, donde pudo desarrollar lo más importante de su obra matemática. Allí caería en un estado de depresión, la falta de reconocimiento de su trabajo matemático por parte de la Academia de Ciencias, el alejamiento de su familia y amigos, y el temor a ser asesinado por la policía política (estaba convencido que él era el objetivo en la cárcel de la bala disparada por un francotirador), por lo que, estando borracho, intentó suicidarse con un cuchillo, pero sus compañeros consiguieron evitarlo.
En marzo de 1832 una epidemia de cólera se desató en París, y los prisioneros más jóvenes fueron liberados. Galois fue trasladado a la casa de reposo del doctor Faultrier, donde se enamoró de su hija, Stéphanie. No se conoce mucho sobre la relación entre ambos, salvo por dos cartas que ella le escribe, pero que el joven destruye y que él mismo reescribe después de su puño y letra. En ellas Stéphanie le pide romper sus relaciones y que volvieran a ser de nuevo amigos. Al parecer la hija del médico estaba comprometida con Pescheux d’Herbinville (según Dumas, este era un camarada republicano, uno de los diecinueve oficiales de la Guardia Nacional absueltos por conspiración), quien al descubrir la infidelidad de su novia reta a Évariste a un duelo al alba.
D’Herbinville era uno de los mejores tiradores de Francia, por lo que Galois no dudó sobre cuál sería el resultado del duelo. Por este motivo, se pasó la noche anterior escribiendo tres cartas a sus amigos. La primera estaba dirigida “A todos los republicanos”, y en ella se puede leer “Pido a mis amigos patriotas que no me reprochen morir por otra cosa que no es mi país. Muero víctima de una infame coqueta y sus dos engañados”. Otra carta la dirige a dos amigos suyos, a quienes les anuncia su muerte como consecuencia de un duelo al que “ha sido imposible negarme”. Y una tercera carta a Auguste Chevalier en la que se recogen sus investigaciones matemáticas, para que se las envíe a los matemáticos Gauss y Jacobi.


En la mañana del 30 de mayo de 1832, el joven matemático se presentó solo al duelo, no había avisado a nadie, únicamente mandó un mensajero para que informara a su hermano Alfred al terminar el mismo. D’Herbinville y Galois se pusieron a veinticinco pasos de distancia y dispararon sus pistolas. El primero salió ileso, mientras que el matemático fue alcanzado en el estómago, quedando tirado y malherido en el suelo, sin que nadie le atendiera. Horas más tarde le llevarían al hospital, pero ya era demasiado tarde, se le había producido una peritonitis y moriría al día siguiente. Sus últimas palabras dirigidas a su hermano fueron “No llores, me hace falta todo el ánimo para morir a los veinte años”.
Fue enterrado en el cementerio de Montparnasse, en el que se reunieron más de 2.000 republicanos para rendirle homenaje. Como era de esperar, al término del mismo se produjeron enfrentamientos entre los camaradas republicanos de Évariste y los agentes de la policía que les estaban controlando.
Sin embargo, a día de hoy sigue sin estar muy claro el motivo del duelo, podía ser fruto de la disputa amorosa por Stéphanie, pero como menciona Fernando Corbalán en su libro Galois, revolución y matemáticas, existen otras dos hipótesis. Una, que el duelo amoroso fuera una encerrona de la policía política de Luis Felipe, como así lo creían sus camaradas republicanos durante su entierro, ya que Galois, en su lecho de muerte, le había dicho a su hermano Alfred que quien le había herido era un policía. Sin embargo, esta no era una práctica habitual de la policía política, y cuando posteriormente se publicó la lista de agentes secretos, d’Herbinville no estaba en ella.
La última hipótesis es que se podría tratar de un suicidio político. Era habitual que cuando había un entierro de algún republicano víctima de la represión se produjeran revueltas populares, y de hecho así ocurrió cuando el padre da Galois se suicidó algunos años antes. A lo que podemos añadir la situación depresiva del joven Évariste. Por lo que, Galois y sus compañeros republicanos pudieron organizar todo un montaje alrededor del duelo para provocar el levantamiento en las calles de París. En el periódico progresista de Lyon, Le Précurseur, se publicó lo siguiente: “El joven Galois se ha batido con un viejo amigo suyo, un hombre muy joven, como él, y miembro de la Société des Amis du People […] Cada uno de ellos estaba armado con una pistola y ha hecho fuego a bocajarro. Sólo una de estas pistolas estaba cargada”. Aunque quien sabe si esto último sería cierto.
Pero no ha sido Évariste Galois el único matemático que ha estado en prisión. Por ejemplo, el matemático y médico galés Robert Recorde (1510-1558), también pasaría por la cárcel.
A Recorde le debemos el signo “=” para la igualdad. Lo introdujo en su libro de álgebra “The Whetstone of Witte” (1557). Decía que no había dos cosas más iguales que dos líneas paralelas, por ese motivo introdujo el signo “=” para denotar la igualdad entre dos cosas. En los libros impresos mucho antes de la introducción del símbolo “=” de Recorde, e incluso más de un siglo después, se utilizaban palabras como “aequales”, “aequantur”, “esgale”, “faciunt”, y otras, para expresar cuando dos cosas eran iguales, incluso la abreviatura “aeq.”. Es decir, en los libros científicos se escribían “a equale b”, o “a aeq. b”, pero no se utilizaba ningún símbolo para la igualdad.
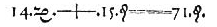
Robert Recorde trabajó de matemático, de médico (para el rey Edward VI y la reina María) y en 1549 fue nombrado interventor de la Bristol Mint (minas y montes). De esa época es su fatal enemistad con cierto conde, al negarse a desviar dinero para apoyar al ejército de este en una sublevación, por entender que no era una orden directa del rey. Recorde fue acusado de traición y acabó 60 días en la cárcel.
Esa enemistad siguió creciendo hasta el punto que acabó en prisión supuestamente por deudas, o por algún delito en relación a su trabajo en Irlanda como interventor de minas y montes, aunque parece ser que realmente fue consecuencia de su enemistad con el mencionado conde (que gracias a sus jugadas políticas habría subido muy alto a nivel político, dentro de la corte inglesa). La salud del matemático se fue deteriorando en prisión, donde moriría.
Pero cambiemos un poco de estilo de muerte. Las personas dedicadas a las matemáticas también pueden morirse de formas más normales, como por ejemplo, en su cama a una edad avanzada, de un ataque al corazón o fruto de un accidente. Y este fue el caso del matemático polaco Witold Hurewicz (1904-1956), experto en Topología Algebraica.
Hurewicz murió al caerse accidentalmente de una pirámide Maya en Uxmal, Yucatán (México). Hurewicz había ido a México a participar en un Simposio de Topología Algebraica organizado en la UNAM, Universidad Nacional de México, en el que dio su conferencia inaugural. Era además un apasionado de la arqueología, lo que por desgracia le llevaría a su muerte a la edad de 52 años, con mucha vida –también matemática- aún por delante.
Este es uno de esos personajes de los que se cuenta que era muy despistado. En el libro Los matemáticos no son gente seria, de Claudi Alsina y Miguel de Guzmán, afirman que entre sus despistes, el que más fama alcanzó fue el siguiente. En cierta ocasión realizó un viaje en coche a la ciudad de Nueva York y una vez instalado allí se olvidó totalmente del coche, tal es así, que cuando regresó de nuevo a su casa, lo hizo en tren. Como adorno a tal despiste, a su regreso a casa y tras comprobar que su coche no estaba en el garaje denunció ante la policía el robo de su vehículo.
Pero también existen casos de muertes absurdamente lógicas. Kurt Gödel (1906-1978) fue un matemático eminente y quizás el lógico más brillante del siglo XX. Sus teoremas de indecibilidad y de incompletitud significaron una gran convulsión en el mundo de las matemáticas.
Gödel sufría un estado paranoico, y creía que la gente estaba empeñada en envenenarlo, motivo por el cual su esposa Adele probaba la comida antes que él, que entonces se sentía tranquilo y comenzaba a comer. En cierta ocasión que su esposa estaba en el hospital recuperándose de una operación quirúrgica, Gödel dejó de alimentarse. Adele no pudo convencerle de que comiera y el 19 de diciembre de 1977 fue hospitalizado. Pero siguió negándose a tomar alimento. Murió el 14 de Enero de 1978. Fue lógico hasta la muerte… ¿¡o no!? Durante su vida sufrió también de crisis nerviosas y de hipocondría.

Existen muchas muertes de matemáticos y matemáticas de las que podríamos hablar, aunque eso tendrá que ser en otra ocasión. Para concluir esta entrada del Cuaderno de Cultura Científica, vamos a terminar con la no-muerte de un gran matemático, el alemán Richard Dedekind (1831-¿?), sobre la cual he leído en Mathematical Circles. Trabajó principalmente en álgebra y teoría de números algebraica, y a él le debemos los fundamentos del sistema numérico (definiciones de números reales y naturales).
Al parecer en el año 1904 se publicó un calendario que recordaba las fechas de nacimiento o muerte de algún matemático, o matemática, para cada día del año. El 4 de septiembre, y se mencionaba el año 1899, estaba marcado como el de la muerte de Richard Dedekind. Cuando el matemático aludido se enteró de su presencia en el mencionado calendario, escribió al editor del mismo diciéndole que si bien la fecha del 4 de septiembre podía ser correcta, sin lugar a dudas el año 1899 no lo era, ya que en ese tiempo gozaba de buena salud y si recordaba bien aquel día había disfrutado de una estimulante discusión matemática con su invitado a cenar, que no era otro que su amigo Georg Cantor, quien, añadió Dedekind, aprovechó la oportunidad para asestar un golpe mortal no a su anfitrión sino a un error matemático que él había cometido.
El calendario pasó a estar completamente equivocado el 12 de febrero de 1916, día en que falleció realmente matemático Richard Dedekind.
Referencias:
1.- Howard W. Eves, Mathematical Circles, volumenes I y II, The Mathematical Association of America, 2003.
2.- Juan Luis García Hourcade, biografía de Nicolás Copérnico en divulgamat.
3.- VVAA, “El rostro humano de las matemáticas”, Nivola, 2008. (coordinada por Raúl Ibáñez y Antonio Pérez) Versión on line en divulgamat
4.- Fernando Corbalán, biografía de Évariste Galois en divulgamat.
5.- Fernando Corbalán, Galois, revolución y matemáticas, Nivola, 2010.
6.- Simon Singh, El enigma de Fermat, Planeta, 1998.
7.- Claudi Alsina, Miguel de Guzmán, Los matemáticos no son gente seria, Rubes, 1998.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Hitos en la red #18 | Naukas
[…] lo hace estudiar matemáticas. Eso sí parece que cada vez se confirma más la conjetura de que Los matemáticos también mueren (no sé si alguien habrá publicado la demostración en alguna revista seria). Por Raúl […]
María
Me encantan sus artículos, los disfruto montones!
Gracias