Los juegos de ingenio y desafíos matemáticos son una potente herramienta de divulgación de las matemáticas. La mayoría de las personas no se puede resistir a intentar resolver un interesante reto de ingenio. Además, el esfuerzo realizado en la búsqueda de la solución del mismo se ve recompensado cuando finalmente se resuelve, con una gran satisfacción y una extraña sensación de felicidad.

La matemática recreativa es casi tan antigua como la propia matemática. Ya aparecen problemas matemáticos recreativos en el Papiro de Rhind (escrito por el escriba Ahmes en el siglo XVI a.c.) y en antiguas tablillas babilónicas (1.800 – 1.600 a.c.). Aunque una cuestión interesante es cuando estos desafíos matemáticos se convirtieron en populares y de interés para la sociedad en su conjunto. En el mundo occidental se vivió una época de esplendor en el siglo XIX, cuando grandes nombres de la matemática recreativa, como Lewis Carroll (1832-1898), Sam Loyd (1841-1911), Éduoard Lucas (1842-1891) o Henry E. Dudeney (1857-1930), entre otros, publicaban problemas de ingenio en periódicos y revistas dirigidos al público general, y editaban publicaciones dedicadas únicamente a proponer retos matemáticos a sus lectores y lectoras.

Sin embargo, hoy no vamos a hablar de la matemática recreativa occidental, sino de un hermoso ejemplo de cómo los desafíos matemáticos se convirtieron, entre los siglos XVII y XIX, en elementos de interés para toda la sociedad japonesa, que incluía por ejemplo a samuráis, comerciantes o campesinos, los sangakus (cuyo significado literal es “tablillas matemáticas”).

La matemática japonesa de ese tiempo, así como los sangakus, que serían expresiones de la matemática popular, fueron consecuencia en gran medida de las circunstancias especiales del período Edo en Japón. Tras la batalla de Sekigahara en la cual el daimyo (señor feudal) Tokugawa Ieyasu derrotó a su rival Toyotomi Hideyoshi, el ganador se convirtió en Shogun de Japón, estableciendo el shogunato Tokugawa que duró prácticamente tres siglos, de 1603 a 1868. Tokugawa Ieyasu se estableció en una pequeña ciudad fortaleza en el centro de Japón, conocida como Edo (se pronuncia “yedo”), hoy en día Tokio. Por este motivo a este periodo se le conoce como el período Edo.

El shogunato Tokugawa se cerró al mundo, con algunas pequeñas excepciones como el comercio con Corea y China. En la década de 1630, Tokugawa Iemitsu, nieto de Ieyasu, firmó una serie de decretos que prohibían el envío de buques al extranjero, así como que cualquier japonés viajase fuera de Japón, bajo pena de muerte. El final del shogunato tuvo lugar una década después de la convención de Kanagawa en la que el comodoro Matthew C. Perry rompió el aislamiento internacional de Japón.

Aunque pueda sorprender este aislamiento del mundo tuvo algunas consecuencias positivas para Japón. Durante más de 250 años no hubo conflictos con territorios extranjeros, por lo cual al período Edo se le conoció como la “Gran Paz”. Así mismo, la cultura experimentó un brillante florecimiento, de hecho a los últimos años del siglo XVII se les conoció como el Genroku (Renacimiento). Las artes sufrieron un gran desarrollo, en especial, la danza Noh, las ceremonias del té, las decoraciones florales, la arquitectura de los jardines, las estampas japonesas ukiyo-e (o “pinturas del mundo flotante”), las shunga (o “imágenes de primavera”), que eran representaciones visuales del sexo, o los haikus.

El mencionado aislamiento durante el período Edo también tuvo su influencia en la ciencia y las matemáticas. En particular, durante el Genroku empezó a florecer lo que se ha llamado la “matemática tradicional japonesa”, completamente aislada de la matemática occidental. Y es a ese período al que corresponden los sangokus, una expresión popular de la “matemática tradicional japonesa” en forma de desafíos matemáticos, especialmente geométricos.

La tradición de colgar tablillas de los templos budistas y los santuarios sintoístas, proviene de la costumbre del sintoísmo, religión nativa del Japón que se fundamenta en la existencia de los kami –divinidades o seres espirituales-, de hacer una ofrenda de caballos a los kami, animales considerados intermediarios entre este mundo y el de los kami, ya que si no era posible ofrecer un caballo real, la ofrenda consistía en imágenes de caballos pintadas sobre tabillas de madera o papel que se colgaba de los santuarios. Muchas tablillas de los siglos XV, y anteriores, contenían pinturas de caballos (“ema”, literalmente “pinturas de caballos”). En algún momento en el inicio del período Edo se empezaron a realizar también ofrendas de tablillas con desafíos matemáticos, los sangakus. Luego los problemas geométricos debían complacer a los kami.

Por lo tanto, un sangaku (palabra japonesa cuyo significado literal, como hemos mencionado ya, es “tablilla matemática”) era una tablilla que contenía problemas matemáticos y que se colgaba de los aleros de los templos budistas y los santuarios sintoístas. No se conoce con exactitud cuando los problemas matemáticos escritos sobre una tablilla de madera se convirtieron en motivo de ofrendas religiosas. El primer sangaku del que se tiene conocimiento es de 1668 y fue mencionado por el matemático Yamaguchi Kanzan (1781-1850) en su diario, aunque la tablilla matemática más antigua conservada data de 1683 y fue encontrada en la prefectura de Tochigi (más al norte de Tokio y debajo de la prefectura de Fukushima). Según el libro Sacred Mathematics. Japanese Temple Geometry se conservan más de 880 tablillas matemáticas, aunque se perdieron un mínimo de 1.738. Y la primera colección de problemas matemáticos escritos en los sangakus fue Shinpeki Sanpō (Problemas matemáticos suspendidos en el Templo), publicada por el matemático japonés Fujita Kagen (1765-1821) en 1789.

Normalmente cada sangaku contenía los enunciados de varios problemas, que solían estar acompañados de coloridos diagramas y la mayoría de las veces las respuestas a los problemas, aunque rara vez las soluciones detalladas de los mismos.

La mayoría de los problemas que aparecen son geométricos, más concretamente de geometría euclidiana (es decir, la geometría normal, la del plano y el espacio), y en ellos solían aparecer circunferencias, elipses, triángulos, cuadrados, esferas, cubos y otras figuras, que normalmente se colocaban unas dentro de otras o tocándose en una cierta posición, y se pedía calcular alguna información relacionada con la distribución dibujada. Aunque también existían otros tipos de problemas, por ejemplo, problemas diofánticos, es decir, relacionados con ecuaciones algebraicas en las que se buscaban soluciones de números enteros. Muchos de los problemas planteados en las tablillas matemáticas provenían de nuevos resultados de la “matemática tradicional japonesa”.

Pero, ¿quienes fueron las personas que escribieron estas tablillas matemáticas? Estas solían estar escritas en Kanbun, una lengua antigua con caracteres y gramática china que jugó el mismo papel que el Latín en Europa, por lo que se sabe que las personas que solían escribir los sangakus solían ser personas con una buena educación, muchos eran miembros de la clase samurai. De hecho, durante el periodo Edo, muchos samuráis acabaron convirtiéndose en matemáticos. Aunque en general las tablillas matemáticas fueron escritas por todo tipo de personas, jóvenes, estudiantes, campesinos, granjeros, mercaderes y también mujeres. Estaban dirigidos a todo el mundo, a todas las personas que estuviesen interesadas.

Para finalizar esta entrada del Cuaderno de Cultura Científica dedicada a esta joya de la matemática recreativa popular que son los sangakus, vamos a mostrar algunos ejemplos, para quienes están leyendo estas líneas se puedan entretener y divertir con su resolución.

El primer problema que se presenta pertenece a una tablilla matemática de 1824, encontrada en un templo de la prefectura de Gunma, y que en Japón se conoce como el teorema de Mikami y Kobayashi. Dice así: “las tres circunferencias de la figura son tangentes entre sí y también a la recta horizontal, calcúlese la relación entre los radios de las tres circunferencias”.

La solución es la siguiente. Si se denotan los radios de las tres circunferencias como r₁, r₂ y r₃, entonces . Este problema es un caso particular del problema de las cuatro circunferencias tangentes de Descartes.

El siguiente problema, propuesto por Watanabe Kiichi, aparece en un sangaku del templo budista de Abe Monju-in, en la prefectura de Tokushima, colgado en 1877. El problema dice así: “Considérese, como se muestra en la imagen, un triángulo equilátero de lado t, un cuadrado de lado s y un círculo, que se tocan entre sí, dentro de una triángulo rectángulo ABC, con lado vertical a. Encontrar t en función de a”.

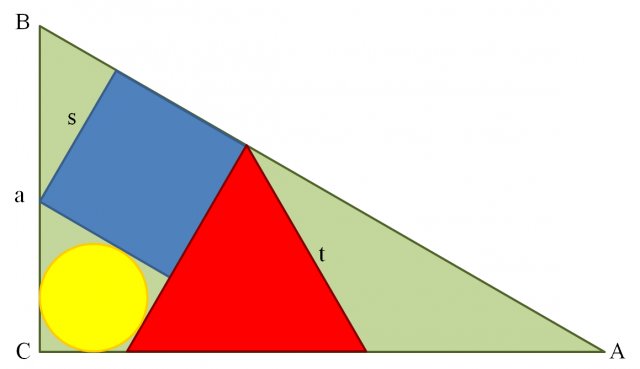
La solución es .

En un sangaku colgado en 1842 en el templo Atsuta, situado en la ciudad de Nagoya, prefectura de Aichi se incluye este problema propuesto por Nagata Takamichi. Dice así: “Tómese un punto C en el segmento AB, como se muestra en la imagen, y dibújese dos circunferencias de diámetro AC y BC, que son tangentes en C. Desde el punto A, trácense dos rectas tangentes a la circunferencia s (de diámetro AC) y desde el punto B dos rectas tangentes a la circunferencia t (de diámetro BC). Ahora se consideran dos circunferencias de radios p y q, que tocan cada una a cada par de las rectas tangentes y pasan por el punto C. Demuéstrese que p=q, para cualquier C”.

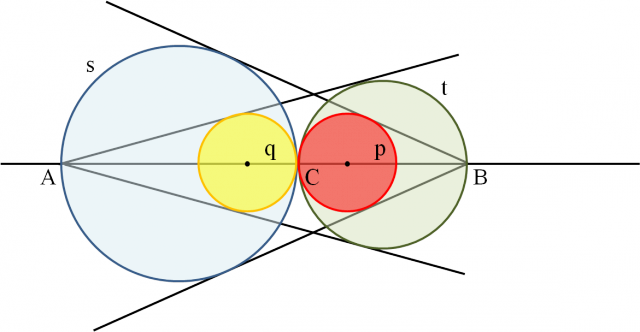
El siguiente problema pertenece a una tablilla matemática colgada en 1873 en el santuario Katayamahiko, en la prefectura de Okayama, y dice así: “Sea un campo con la forma de un triángulo rectángulo ABC, con AC = 30 m y BC = 40 m. Como se muestra en la imagen, se quiere trazar un camino DEHKJIGF de anchura 2m, de forma que los tres trozos de campo que quedan tengan el misma área. Encontrar BE, DE, HC, JC, AI y FG”.

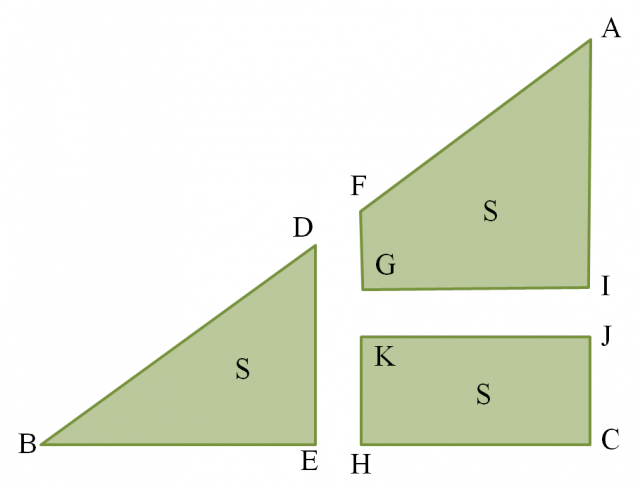
La respuesta es: BE = 21,77; DE = 16,33; HC = 16,23; JC = 10,96; AI = 17,04 y FG = 4,87.

Y por último, un problema incluido entre los que son un poco más difíciles en el libro Sacred Mathematics. Japanese Temple Geometry. Este problema fue propuesto por Ikeda Sadakazu en 1826 y se colgó en un santuario de la ciudad de Azabu, en la prefectura de Tokio. Este problema y otros 24 colgados entre los años 1808 y 1826 fueron recogidos en el libro Shamei Sanpu (Matemática sagrada), escrito en 1927 por Shiraishi Nagatada (1795-1862). El problema dice así: “Sean tres cuadrados de lados a, c y d, apoyados en una línea recta l, y que cada uno de ellos toca en un vértice a un cuadrado de lado b, como se muestra en la imagen, demuéstrese que b = 2d”.

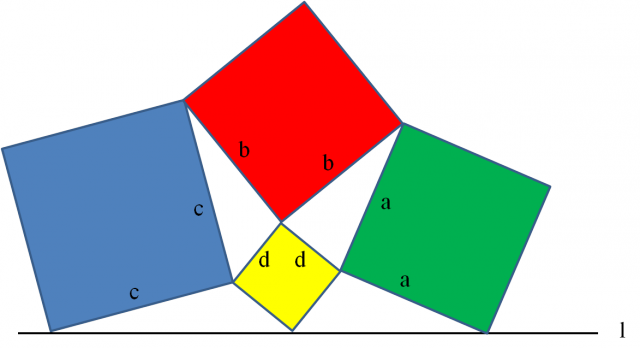
Vamos a incluir la solución que se presenta en el libro Sacred Mathematics. Japanese Temple Geometry y que dice que es trivial según el diagrama siguiente.

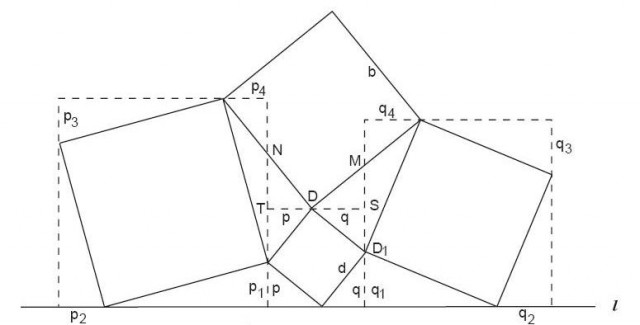
Según la anterior imagen q = q₁ = q₂ = q₃ = q₄, luego M es el punto medio de ese lado. Por tanto, MD = b/2. De igual forma, p = p₁ = p₂ = p₃ = p₄, luego N es el punto medio de ese lado y ND = b/2. De forma que los triángulos MSD y NTD son congruentes, con MS = p y NT = q. Por lo tanto, S es el punto medio de MD₁ y MS = SD₁ = p, lo que significa que los triángulos MDS y DSD₁ son congruentes, luego b = 2d.

El libro Sacred Mathematics. Japanese Temple Geometry es una excelente fuente de información sobre los sangakus, así como sobre la matemática tradicional japonesa del periodo Edo, pero además incluye una amplia colección de problemas, sencillos, difíciles y muy difíciles, con soluciones incluidas.

Al parecer en las últimas décadas se ha producido un renacer de los sangakus. Estos estánsiendo utilizados por los profesores para enseñar geometría a los estudiantes.

Bibliografía

1.- David Singmaster, Sources in Recreational Mathematics, an Annotated Bibliography

2.- Fukagawa Hidetoshi, Tony Rothman, Sacred Mathematics, Japanese Temple Geometry, Princeton University Press, 2008.

3.- Fernando Fouz, Sangaku: Geometría en los templos japoneses, Revista SIGMA, n. 22, p. 173-189, 2003.

4.- José Miguel Figueroa O’Farrill, La geometría sagrada del Japón (conferencia), Universidad de Murcia, 2013.

5.- Rosaline Hosking, Sangaku – Japanese Temple Mathematics (conferencia), University of Canterbury, New Zeland.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica