En mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica “Diseños geométricos de chocolate” hablábamos de algunos diseños geométricos de tabletas de chocolate realizadas por, o para, el maestro chocolatero barcelonés Enric Rovira, como las tabletas de chocolate “Hexàgon Gaudí”, “Pythagoras” o “Chocodosis”.

Sin embargo, en la entrada de hoy volvemos a la forma típica de la tableta de chocolate. Rectangular y marcada por líneas horizontales y verticales, igualmente espaciadas en cada dirección, que generan una red de pequeñas porciones iguales, cuadradas o rectangulares, las onzas, en las que se divide la tableta en cuestión. Y más concretamente, vamos a dedicar este artículo a una serie de juegos de ingenio que se pueden jugar con este tipo de tabletas.

El primero de los juegos que vamos a analizar aquí, suele recibir el nombre “partiendo tabletas de chocolate” (“breaking chocolate bars”) y consiste en lo siguiente. Es un juego para dos personas que, por turnos, se dedican a partir una tableta de chocolate, por ejemplo, de tamaño 6 x 4 (como la que aparece en la imagen siguiente). Pero, solo se puede partir la tableta de chocolate por las líneas horizontales y verticales, como de hecho, se hace en la realidad. Es decir, el corte es de toda la línea, de un lado a otro.

Por ejemplo, en la primera ronda, el primer jugador podría partir por la línea vertical intermedia, generando dos piezas de tamaño 3 x 4, y el segundo jugador tomar una de las piezas 3 x 4, y partirla por la primera línea horizontal, empezando por abajo, generando así una pieza 3 x 1 y otra 3 x 3. En ese punto de la partida, habrá tres trozos de chocolate, de tamaños 3 x 4, 3 x 1 y 3 x 3.

Los jugadores seguirán cortando hasta que solamente queden onzas sueltas, es decir, piezas 1 x 1, y no se pueda partir más. La persona que hace la última división gana, o lo que es lo mismo, pierde el jugador que se queda sin la posibilidad de fragmentar más el chocolate.

Una sugerencia. Elegid bien a la persona con la que queréis jugar, y echad algunas partidas al juego “Partiendo tabletas de chocolate”. De paso podéis aprovechar la ocasión para comer las onzas de chocolate que van quedando. Cuanto más rico sea el chocolate, más interesante (para vuestro paladar) será el juego.

En este juego no se puede quedar en tablas, luego uno de los dos jugadores debe de ganar. La cuestión es si existe una estrategia ganadora para alguno de las dos personas que juegan a “partiendo tabletas de chocolate”. Para resolver esta cuestión vamos a analizar un problema de ingenio relacionado con el mismo. Dice así.

Problema (Partiendo la tableta de chocolate): Si se tiene una tableta de chocolate rectangular típica, de tamaño m x n, que se quiere partir hasta conseguir que todas las onzas estén sueltas, ¿cuál es el número mínimo de troceados (en vertical u horizontal) para conseguirlo?

La solución a este problema es sencilla. Si tenemos en cuenta que cada vez que se parte el chocolate, por una de sus líneas horizontales o verticales, aumenta el número de trozos en uno, y que el número de trozos finales será igual al número de onzas que tiene la tableta, que es el producto m x n, entonces el número de roturas que se realizarán será siempre el mismo, independientemente del procedimiento empleado, y exactamente igual a (m x n-1). Por ejemplo, en el caso de la tableta 3 x 2, esta se parte 5 veces (2 x 3 – 1).

En el libro “Algorithmic puzzles” se plantea una interesante generalización de este problema de ingenio, que consistiría en que se pueden apilar los trozos cortados de la tableta de chocolate y cortarlas al mismo tiempo por una línea horizontal o vertical superpuesta en los diferentes trozos de chocolate apilados.

Supongamos que la tableta de chocolate tiene un tamaño 2ⁿ x 2^m, si la cortamos por la línea vertical central quedarán dos tabletas de tamaño 2^n-1 x 2^m, que podremos superponer para seguir cortando. El número mínimo de cortes, utilizando el apilamiento de los trozos de chocolate generados, para dejar separadas líneas individuales verticales de chocolate es n. De forma similar, para los cortes horizontales. Por lo tanto, el número mínimos de cortes, con apilamiento, para conseguir que las onzas queden sueltas, serían n + m.

Ese mismo argumento nos dice que para el caso general de una tableta de chocolate de tamaño (2ⁿ +k) x (2^m +h), el número mínimos de cortes, con apilamiento, serían (n+1) + (m+1).

Volviendo al juego “Partiendo tabletas de chocolate”, como el número de veces que se parte la tableta, para conseguir que las onzas queden sueltas, es siempre igual (como hemos visto en la solución del problema de ingenio que lleva su mismo nombre), cual de los jugadores gana el juego está completamente determinado de antemano, antes de empezar a jugar, solo hay que saber quién empieza. Y además, no hay necesidad de una estrategia ganadora, el resultado es siempre el mismo se juegue como se juegue. Por ejemplo, para la tableta 6 x 4, en la que se realizan 47 particiones, el ganador es siempre el primer jugador. En general, si el producto m x n es par, ganará el primer jugador, mientras que si m x n es impar, ganará el segundo.

Una variación del anterior juego podría ser la siguiente. De nuevo, dos jugadores que, por turnos, se dedican a partir una tableta de chocolate, por ejemplo, de tamaño 5 x 10, por las líneas horizontales y verticales. Pero ahora ganará el jugador que primero consiga obtener una onza de chocolate separada del resto.

El siguiente juego, que recibe el nombre de “yucky choccy” (que podríamos traducir como “chocolate asqueroso”), lo descubrí en el excelente libro “Locos por las matemáticas” de Ian Stewart, junto al juego “chomp” del que hablaremos después. De nuevo, este juego se juega con una tableta de chocolate rectangular, o cuadrada, típica, pero con la particularidad de que la onza de una de las esquinas (en nuestra imagen siguiente es la de arriba a la izquierda) tiene mal sabor, está asquerosa (ya sea porque le ha caído un poco de jabón, como dice Stewart, o porque tiene una almendra podrida, si el chocolate es con almendras, o lo que consideremos oportuno).

Los jugadores, por turnos, partirán el chocolate por una línea horizontal o vertical (de nuevo, debe de ser toda la línea), con la intención de comerse uno de los trozos de chocolate que parten, en concreto el que no incluya la onza asquerosa. El jugador que se come la onza asquerosa pierde.

De nuevo, en este juego no hay posibilidad de tablas, de empate, por lo tanto siempre gana uno de los dos jugadores. A continuación, vamos a intentar descubrir la estrategia ganadora para el “yucky choccy”, es decir, la forma de ganar siempre.

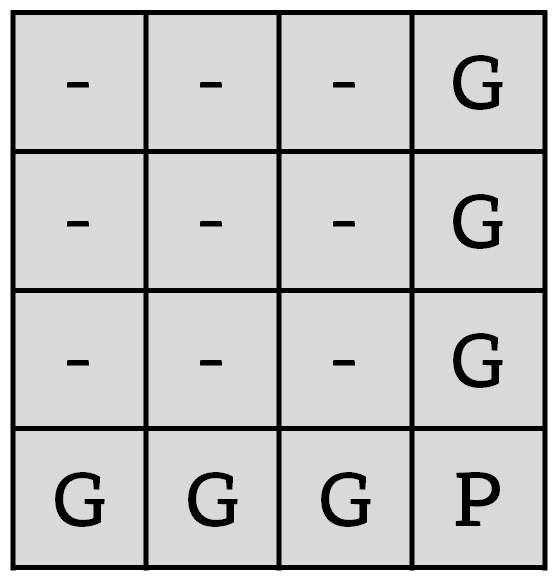
Analicemos el caso particular de la tableta de chocolate 4 x 4 con la onza asquerosa en la esquina superior izquierda. Para empezar nos fijamos en el diagrama de todas las configuraciones posibles del juego (que se muestran en la anterior imagen) y vamos a nombrar cada configuración del juego de la siguiente forma:

i) una configuración es ganadora (y utilizaremos la letra G para marcarla) si el jugador al que le toca mover puede realizar algún movimiento para dejarle a su adversario una configuración perdedora;

ii) una configuración es perdedora (y utilizaremos la letra P) si cualquier movimiento que realice el jugador le deja a su rival en una configuración ganadora.

Estas parecen definiciones circulares, ya que una depende de la otra, sin embargo, son definiciones recursivas, que se apoyan en el hecho de que conocemos cómo es la última configuración. En el juego “chocolate asqueroso” la última configuración es perdedora, puesto que al final solo queda la onza asquerosa, y al que le toca mover no le queda más remedio que comérsela.

Veamos, en el diagrama anterior, qué configuraciones son ganadoras y cuales perdedoras. La configuración final (abajo a la derecha), es una configuración perdedora. Además, claramente las configuraciones que están encima de esa última configuración, y las que están a su izquierda, son todas configuraciones ganadoras, puesto que se puede cortar todo el chocolate bueno, y dejar solo la onza desagradable, la configuración final, y como hemos dicho, perdedora.

Si seguimos razonando de forma recursiva, desde las últimas configuraciones hacia las primeras, ¿cómo es la configuración en la que queda un trozo de tamaño 2 x 2? Hagamos el corte que hagamos, ya sea en horizontal o vertical, se pasa a una configuración ganadora, luego esa será una configuración perdedora. Y de paso, por el mismo razonamiento que antes, las configuraciones que están encima de ella o a la izquierda, son configuraciones ganadoras.

Siguiendo el razonamiento, podemos clasificar todas las configuraciones que aparecen en el diagrama de la tableta de chocolate 4 x 4, como aparece en la siguiente imagen.

Como vemos la posición inicial es “perdedora” y por tanto, existe una estrategia ganadora para el segundo jugador, cada vez que el primer jugador mueve a una configuración ganadora, el segundo solo tiene que volver a mover a una posición perdedora. Si volvemos al ejemplo de partida vista anteriormente, el segundo jugador no ganó porque en su primer movimiento pasó de una posición perdedora a otra configuración perdedora, dándole la opción al primer jugador de darle la vuelta a la partida.

Si la tableta de chocolate es cuadrada, como en el ejemplo anterior, existe una estrategia ganadora para el segundo jugador, sin embargo, si la tableta es rectangular, no cuadrada, la estrategia ganadora existe para el primer jugador, puesto que la configuración inicial es ahora ganadora.

Imagen 10 (Pie de imagen: Configuraciones posibles del juego “chocolate asqueroso” para una tableta 5 x 4, con la onza asquerosa en la parte superior izquierda, y cuadro con la clasificación de las configuraciones en ganadoras o perdedoras).

Existe una forma de recordar si las configuraciones son ganadoras o perdedoras. Si nos fijamos bien, las configuraciones perdedoras son aquellas en las que el trozo de tableta que queda es “de tipo cuadrado”, es decir, de la forma n x n, mientras que las “de tipo rectangular”, de la forma m x n (con m y n distintos), son ganadoras.

Podemos plantearnos ahora qué ocurre con este juego si la onza asquerosa se encontrase en otra posición que no fuese una de las cuatro esquinas. Aunque ese es un problema que os dejo para quienes estáis leyendo esta entrada del Cuaderno de Cultura Científica.

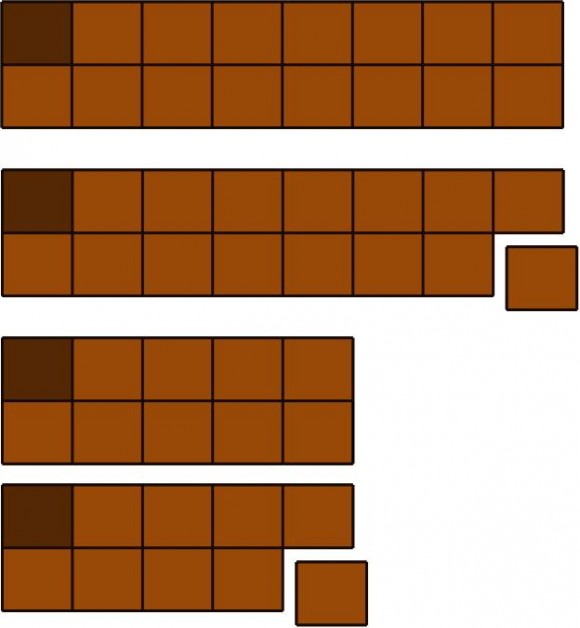
Nuestro último juego con tabletas de chocolate es el “chomp” (esta palabra se traduce como “pegar un mordisco”). Las reglas del “chomp” son similares a las del juego “chocolate asqueroso”, con la diferencia de que ahora cada movimiento consiste en quitar un trozo rectangular de chocolate de la siguiente forma. Si la onza asquerosa esta en la esquina superior izquierda, entonces el jugador que mueve elije una onza y se retiran todas las onzas que están debajo y a la derecha de la onza en cuestión, como se muestra en la imagen.

Una vez más, es un juego que no puede quedar en tablas. Vamos a ver, mediante el argumento llamado “robo de estrategia”, que el primer jugador tiene una estrategia ganadora.

Imaginemos que no es así, y que existe una estrategia ganadora para el segundo jugador. Entonces, la configuración inicial es una configuración perdedora. Supongamos que el primer jugador hace un primer movimiento que consiste en quitar la onza de chocolate que está en el vértice diagonalmente opuesto al de la onza asquerosa, como se muestra en la imagen siguiente, entonces esta configuración debería de ser ganadora. Por lo tanto, el segundo jugador podrá realizar un movimiento (dentro de su estrategia ganadora) a una configuración perdedora, el que aparece en la imagen o similar.

Pero en tal caso, el jugador uno podía haber movido inicialmente de forma que llegase directamente a esa configuración, de la manera que se indica en la siguiente imagen, dejándole a su adversario una configuración perdedora, y por tanto, la configuración inicial debería ser ganadora.

El problema de este argumento que nos muestra que existe una estrategia ganadora para el primer jugador en el juego del “chomp”, es que no nos da información sobre cual es esa estrategia. De hecho, no se conoce cual es la estrategia ganadora en general, solo para algunos casos particulares, como las tabletas cuadradas o las que tienen dos filas, y algunos otros casos.

Si tenemos una tableta de chocolate cuadrada, la estrategia ganadora (para el primer jugador) es muy sencilla, y se basa en la simetría. El jugador que mueve primero debe de elegir la onza que está al lado diagonalmente de la onza de chocolate asquerosa para marcar el corte de chocolate de su jugada. De esta forma, quedan determinadas dos zonas lineales, aisladas la una de la otra, de onzas buenas, una hacia abajo de la onza de mal sabor y la otra a la derecha. La táctica del primer jugador será entonces hacer siempre lo mismo que lo que haga el segundo, pero en el “brazo” opuesto, con lo que se asegura quitar la última onza buena disponible.

Si se juega al “chomp” sobre una tableta de chocolate que solamente tenga dos filas, el primer movimiento del jugador que empieza debe de ser quitar la onza de la esquina diagonalmente opuesta a la de la onza asquerosa. Si la tableta es de tamaño 2 x 2, esa es precisamente el primer movimiento de la estrategia ganadora que hemos visto antes. En general, el primer movimiento del segundo jugador solo puede ser de dos tipos.

La primera posibilidad sería eliminar onzas de una sola fila, con lo cual el primer jugador debería realizar un movimiento que deje una situación similar a la de su primer movimiento, aunque con menos trozo de tableta (véase la siguiente imagen).

Mientras que la segunda posibilidad del primer movimiento del segundo jugador, sería eliminar onzas de las dos filas, con lo cual la configuración quedaría similar a la inicial, aunque con un trozo menos de tableta, y el primer jugador hará de nuevo un movimiento como el inicial, es decir, quitar la onza de la esquina opuesta a la onza problemática. En cualquiera de los dos casos, se termina llegando a la configuración de una tableta 2 x 2, en la que ya sabemos que gana el primer jugador, o a la configuración de una onza buena y la otra asquerosa, que sigue siendo buena para el primer jugador.

Doron Zeilberger, de la Temple University desarrolló un programa que analizaba el caso del juego del “chomp” para tabletas de chocolate de tres filas, resultados que fueron ampliados por Xinyu Sun, para cualquier número de filas.

Para terminar, os dejo con otro diseño matemático de una “tableta” de chocolate, la tableta “Pie chart” (o “gráfico circular”).

Bibliografía

1.- Dimitri Fomin, Sergey Genkin, Illia Itenberg, Círculos matemáticos, Biblioteca de Estímulos Matemáticos, SM-RSME, 2012.

2.- Berkeley Math Circle

3. Anany Levitin, María Levitin, Algorithmic puzzles, Oxford Univ. Press, 2011.

4.- Ian Stewart, Locos por las matemáticas, Crítica, 2005.

5.- Doron Zeilberger, Three-Rowed chomp, Adv. Applied Math. 26 (2001), pag. 168-179.

6.- Xinyu Sun, Improvements on Chomp. Integers 2, G1 (2002).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Esta entrada participa en la Edición 5.7: Alan Turing del Carnaval de Matemáticas, cuyo anfitrión es el blog El zombi de Schrödinger.