Estos días he vuelto a leer algunos de los artículos del interesante libro del divulgador Ian Stewart, “Locos por las matemáticas”, lo que me ha llevado a pensar en escribir una entrada del Cuaderno de Cultura Científica sobre dos de los juegos de ingenio que explica el autor en el libro, el “Chomp” y el “Yucky choccy”, los cuales se juegan con las típicas tabletas de chocolate rectangulares. Pero en ocasiones soy un pelín disperso, y mientras trabajaba en la introducción de este artículo, esta se ha convertido en toda una entrada en la que vamos a hablar de algunos diseños geométricos de las tabletas de chocolate y dejaremos los juegos de ingenio para dentro de quince días.

La geometría de las tradicionales tabletas de chocolate es sencilla y muy práctica. Sencilla porque la tableta tiene forma rectangular y está marcada por líneas horizontales y verticales, igualmente espaciadas en cada dirección, que generan una red de pequeñas porciones cuadradas o rectangulares iguales, las onzas, en las que se divide la tableta de chocolate y que son la unidad mínima para comer este delicioso manjar elaborado con cacao. Y práctica porque esa red de líneas horizontales y verticales permite cortar fácilmente la tableta para comer la porción que mejor se adapte a nuestros deseos.

Sin embargo, las tabletas de chocolate también pueden tener diseños mucho más artísticos, incluso en los que la geometría juega un papel importante. El maestro chocolatero barcelonés Enric Rovira [www.enricrovira.com] desarrolló un proyecto de tabletas de chocolate, llamado “Rajoles d’autor” (en catalán, “rajoles” significa tanto “tabletas” como “baldosas”), en el que un diseñador, o diseñadora, invitado por él, y partiendo de la clásica baldosa barcelonesa (conocida como “Rosa de Barcelona” y cuyo diseño podría ser obra del arquitecto modernista Josep Puig i Cadafalch (1867-1956); que, por cierto, es muy parecida a la típica baldosa de Bilbao), debía de realizar un nuevo diseño para la tableta de chocolate.

Tuve conocimiento de este proyecto que conjuga arte y gastronomía a través de la tableta de chocolate “Pythagoras”, en cuyo diseño participó el matemático eibarrés, Enrique Zuazua (Ikerbasque Research Professor de BCAM – Basque Center for Applied Mathematics [www.bcam.es]). Pero antes de describir este diseño, otra de las creaciones de Enric Rovira del “rajol” de chocolate estaba inspirada, como no podía ser de otra forma, en el mosaico hexagonal de baldosas que el arquitecto barcelonés Antoni Gaudí (1852-1926) creó para los suelos de la Casa Milá, conocida como La Pedrera, que se encuentra en el Paseo de Gràcia de Barcelona.

Este bello embaldosado modernista hexagonal de Antoni Gaudí, a quien tanto le gustaba hacer uso de la geometría en su arquitectura (tanto por motivos estructurales, como estéticos), está relacionado con un interesante resultado matemático. Es bastante conocido que solamente existen tres tipos de embaldosados regulares posibles en los que las baldosas tengan la forma de un polígono regular (que el embaldosado sea regular quiere decir que los lados de las losetas tienen la misma longitud y sus ángulos son todos iguales, y por supuesto estamos hablando de embaldosados en los que el lado de una baldosa se pega completamente con el lado de otra baldosa, y no solo parcialmente). Los tres posibles mosaicos regulares son los que se realizan con triángulos equiláteros, cuadrados y hexágonos regulares.

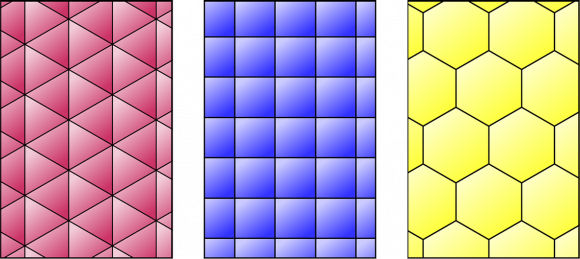
Si nos fijamos en un vértice cualquiera del embaldosado (véase la imagen anterior), en él confluyen un cierto número de baldosas. En el caso del mosaico triangular, en cada vértice se juntan 6 triángulos equiláteros, puesto que el ángulo interior del triángulo equilátero es de 60º, y 6 x 60º = 360º, que es la vuelta completa alrededor del vértice. En la teselación por cuadrados se juntan 4 de estos polígonos, cada uno de ellos con un ángulo interior de 90º en el vértice, y 4 x 90º = 360º. Finalmente, los ángulos interiores de los hexágonos son de 120º, lo cual es coherente con el hecho de que alrededor de cada vértice del embaldosado por hexágonos, hay exactamente tres hexágonos en la “figura” alrededor del vértice (es decir, 120º x 3 = 360º).

La pregunta, llegados a este momento, es si es posible que existan más embaldosados mediante polígonos regulares. La respuesta viene de la mano de la figura del vértice del mosaico, ya que dada una teselación, alrededor del vértice hay un cierto número n de baldosas, luego los ángulos del polígono medirán 360º / n, por lo que veamos qué posibilidades hay… 360º / 2 = 180º (que no nos da ningún polígono), 360º / 3 = 120º (hexágono), 360º / 4 = 90º (cuadrado), 360º / 5 = 72º (no hay ningún polígono regular con un ángulo interior de 72º), 360º / 6 = 60º (triángulo), y no hay más posibilidades que nos den un polígono. En consecuencia, acabamos de demostrar el siguiente teorema:

Los únicos embaldosados regulares lado a lado son los formados con triángulos equiláteros, con cuadrados o con hexágonos regulares.

Por cierto, que los ángulos interiores de un pentágono miden 108º, de un heptágono 128,6º, y en general, para un polígono regular de n lados, es fácil ver que el ángulo interior vale (n-2) x 180º / n.

Pero vayamos al diseño de la tableta de chocolate “Pythagoras”. Esta fue realizada por el diseñador de origen croata Santos Bregaña. En su artículo para el portal divulgamat podéis leer la explicación que él mismo escribió sobre su diseño.

Mientras que en el diseño “chocodosis” de Emili Padrós, también para el proyecto de Enric Rovira, el diseñador se planteaba “porciones caprichosamente diferentes para diferentes deseos” (más adelante volveremos a este diseño), Santos Bregaña plantea el descomponer la tableta de chocolate en porciones triangulares de diferentes formas (es decir, las porciones son triángulos rectángulos con diferentes longitudes de sus lados), pero que tengan la misma superficie, la misma cantidad de chocolate. La idea que se le ocurrió al diseñador que recibió el premio Sphere (Art Director Club de Nueva York) por su trabajo para el restaurante Mugaritz, fue partir del cuadrado inicial (que es la forma de la tableta entera) e ir girándolo, pero sin salirse de su perímetro, es decir, al mismo tiempo que se gira hay que ir reduciendo el cuadrado de tamaño. De esta forma, en cada giro se generan cuadro triángulos rectágulos entre el cuadrado anterior y el que se acaba de trazar (como se muestra en la imagen).

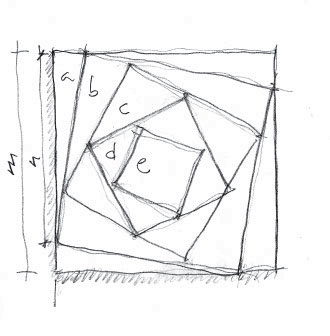
Para realizar esta idea de manera que todos los triángulos que aparecen en los giros, así como los cuatro que generan las diagonales sobre el último cuadrado, el central, tengan la misma superficie, Santos Bragado acudió al matemático Enrique Zuazua, en aquel momento director científico de BCAM, quien ayudó al diseñador a desarrollar la parte matemática de la obra.

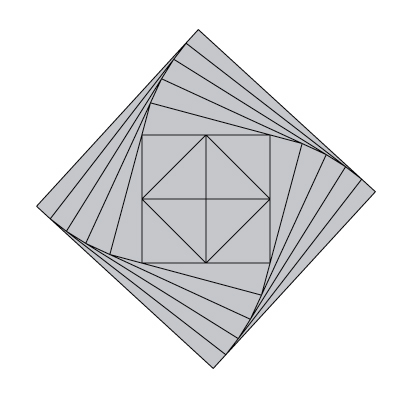
Quizás sea por mi interés por el teorema de Pitágoras (véanse algunas de las entradas anteriores de la sección Matemoción del Cuaderno de Cultura Científica), pero el diseño final de la tableta de chocolate “Pythagoras” de Santos Bregaña, me recuerda al teorema de Pitágoras. La parte central, es decir, los dos últimos cuadrados y las diagonales del cuadrado central, es una demostración visual del teorema de Pitágoras para el caso de un triángulo rectángulo cuyos catetos tengan la misma medida.

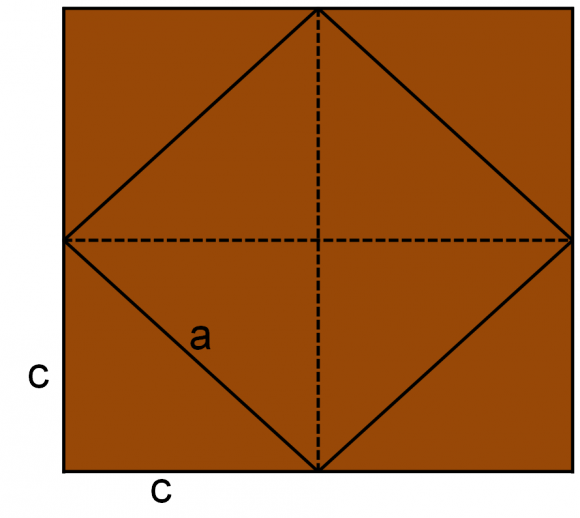
Mientras que cada una de las generaciones de los cuatro triángulos de cada giro, me recuerdan a la demostración visual del teorema de Pitágoras que vimos en el artículo del Cuaderno de Cultura Científica “Pitágoras sin Palabras”, para el caso particular del triángulo rectángulo que se va generando como nueva onza triangular de la tableta de chocolate.

Pero el chocolate es sobre todo una delicia para el paladar, por lo que vamos a recordar aquí las palabras del diseñador Santos Bragado en su artículo para divulgamat…

“Desde el placer físico, bienestar por la ingesta de calorías -por ejemplo en un día fresco de otoño tras subir a un monte-, pasando por las evocaciones y recuerdos que el sabor rescata, previo recorrido fisiológico por los sentidos -sensaciones mecánicas del chocolate bien templado (correctamente cristalizado), aromas complejos, sabores amargos, ácidos, dulces, especiados, florales…… Aromas ocultos que sólo se liberan en el paladar tras fundir las moléculas más grasas que también capturan el azúcar, la teobromina, la feniletilamina, la cefeína, etc. y que abren puertas del cerebro que muestran habitaciones olvidadas, sentimientos delicados y recuerdos antiguos-, el chocolate nos da además toda una suerte de sensaciones físicas que acompañan a emociones, sentimientos y pensamientos entremezclados. Pero de todos estos placeres, nos queda aquel que pitágoras nos reclama como raza celeste, el placer reflexivo que nos permite la contemplación de lo inteligible, de la geometría pura.”

En este camino por los diseños geométricos de tabletas de chocolate del, o para el, maestro chocolatero Enric Rovira, hemos dejado sin visitar el diseño “chocodosis” del diseñador Emili Padrós, en el que se planteaban “porciones caprichosamente diferentes para diferentes deseos”, y al que regresamos brevemente ahora.

Como se puede observar en la imagen, Emili Padrós, con el objetivo de crear porciones de tamaños diferentes para diferentes deseos, como se muestra en la imagen para diferentes momentos del día, crea una red de líneas verticales y horizontales, que no están igualmente espaciadas, por lo que crean porciones rectangulares de diferentes proporciones.

Sería interesante saber qué proporciones ha utilizado para tal fin. La red de líneas verticales y horizontales de su diseño nos recuerda a las dos series de medidas desarrolladas por el arquitecto francés Le Corbusier (1887-1956) en su obra “El Modulor”, y a las rejillas asociadas a las mismas.

El modulor es un sistema de medidas armónicas que parte de la escala humana para ser aplicado universalmente en la arquitectura y el diseño, y que se basa en la proporción áurea y en la sucesión de Fibonacci. Las medidas parten desde la medida del hombre con la mano levantada (226 cm) y de su mitad, la altura del ombligo (113 cm), y multiplicando y dividiendo sucesivamente por el número de oro se obtiene la llamada serie azul, y de la segunda del mismo modo la roja. Y a partir de ellas construye unas rejillas de rectángulos para ser utilizados en arquitectura.

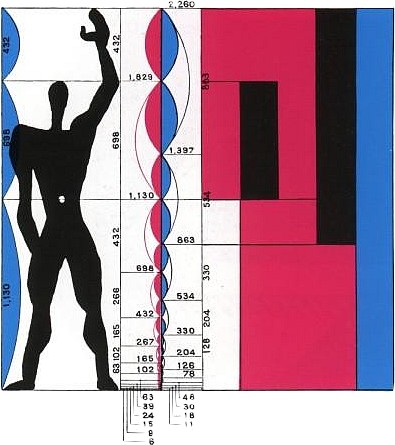
Aunque Padrós no utiliza la distribución de líneas verticales y horizontales de Le Corbusier. Sería interesante conocer cuáles han sido las proporciones que el diseñador ha utilizado para su creación. En qué ha basado su escala.

Para terminar, una pequeña reflexión sobre la revolución que está siendo las impresoras 3D en el mundo del diseño, también en la gastronomía. En la siguiente imagen aparecen figuras geométricas impresas con azúcar en una impresora 3D, pero se podría imprimir también con chocolate.

Y no os olvidéis de que la siguiente semana jugaremos con el chocolate.

Bibliografía

1.- Ian Stewart, Locos por las matemáticas, Crítica, 2005.

2.- Enric Rovira (maestro chocolatero)

3.- Enrique Zuazua (matemático)

4.- Antoni Gaudí, Casa Milá (La Pedrera)

5.- Alexander Aginagalde Nafarrate, Pedro Alegría Ezquerra,

Raúl Ibáñez Torres, Álvaro Lozano Rojo, Marta Macho Stadler, Begirada matematiko bat, Imaginary, Una mirada matemática, (guía didáctica de la exposición), 2011. [PDF]

6.- Santos Bregaña (diseñador)

7.-. Santos Bregaña, Tableta de chocolate Pythagoras, divulgamat, 2011.

8.- Le Corbusier, El modulor (2 volumenes), apostrofe, 2005.

9.- Interior Design

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica