Antes de continuar con la historia iniciada en [1], es conveniente destacar que el teorema de los cuatro colores sobre mapas planos equivale al mismo enunciado sobre mapas esféricos: se demuestra fácilmente usando la proyección estereográfica.
La propiedad clave en la demostración del teorema de los cuatro colores es el teorema de poliedros de Euler que afirma que:
c – a + v = 2,
donde c es el número de caras, ael de aristas y v el de vértices del poliedro estudiado.
Este teorema puede trasladarse a mapas planos. En efecto, dado un poliedro arbitrario, se infla sobre una esfera, se proyecta estereográficamente, y se obtiene su proyección sobre el plano (figura 1).
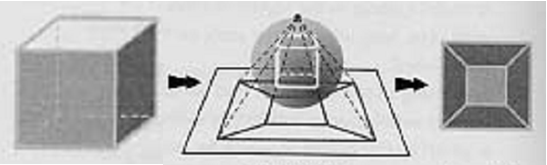
Así, puede hablarse del teorema de Euler para mapas:
r – l + p = 2,
donde r es el número de regiones del mapa, l el de líneas frontera y p el de puntos de encuentro entre dos líneas frontera. En esta fórmula, la región exterior del mapa debe contarse: es la que corresponde a la cara más cercana al polo norte antes de realizar la proyección estereográfica.
Ya podemos continuar con nuestra historia. El abogado Alfred Kempe (1849-1922) se interesó por el problema de los cuatro colores tras la pregunta de Arthur Cayley en la London Mathematical Society en 1878 (ver [1]).

En 1879, Kempe publicó una solución al problema en la revista Nature. Al año siguiente publicó una versión simplificada en los Proceedings of the London Mathematical Society, corrigiendo algunas erratas de su prueba original.
Kempe utilizó la fórmula de Euler para mapas cúbicos (ver [1]) para probar que: Todo mapa tiene al menos una región con como mucho cinco regiones vecinas, es decir, cada mapa contiene al menos un digon, un triángulo, un cuadrado o un pentágono.
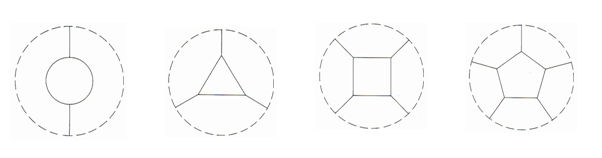
La demostración de Kempe es ahora fácil de entender: si X es una región de un mapa cúbico M, denotamos por v(X) el número de las comarcas que le son colindantes. La prueba se hace por inducción sobre el número de regiones del mapa. ComoMes un mapa cúbico, sabemos que existe una región X con v(X) menor o igual que5. Si suponemos que el mapa M-{X} es 4-coloreable, se trata de ver que entonces M también lo es. Hay tres casos posibles:
CASO 1. Si v(X)= 1, 2 ó 3, disponemos de al menos un color para colorear X con él.
CASO 2. Supongamos que v(X)=4. Antes de continuar, debemos introducir dos nuevos términos. Si Z e Y son dos regiones, por ejemplo, Y de color rojo y Z de color verde en un mapa 4-coloreado, se llama cadena de Kemperojo-verde de Y a Z a un camino que va de Y a Z, alternando los colores rojo y verde. Una componente rojo-verde de Y es el conjunto de todas las regiones Z del mapa, tales que existe una cadena de Kempe rojo-verde de Y a Z.
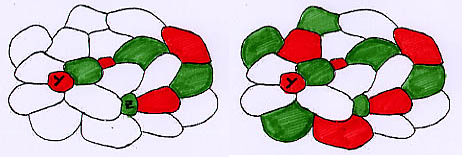
En una componente rojo-verde cualquiera de un mapa 4-coloreado se pueden invertir los colores rojo y verde para obtener un nuevo 4-coloreado, respetando las condiciones del problema de los cuatro colores (ver figura 5).
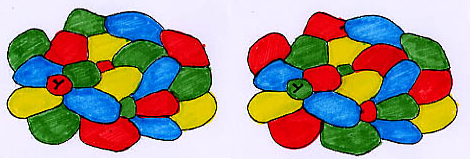
Como v(X)=4, un entorno de X es de la forma indicada en la figura 6:
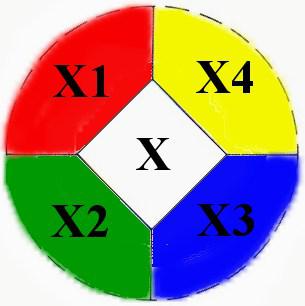
Distinguimos dos posibilidades:
a) X3 no está en la componente rojo-azul de X1. Entonces se invierten el rojo y el azul en esta componente y se libera un color (en la figura 7, el rojo) para X.
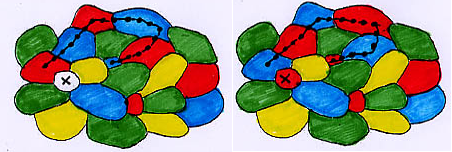
b) X3 está en la componente rojo-azul de X1. Entonces X2no está en la componente amarillo-verde de X4, y se hace un cambio en la componente de X4, rescatando un color (en la figura 8, el amarillo) para X.
CASO 3. Finalmente, supongamos que v(X)=5; un entorno de X es de la forma indicada en la figura 9:
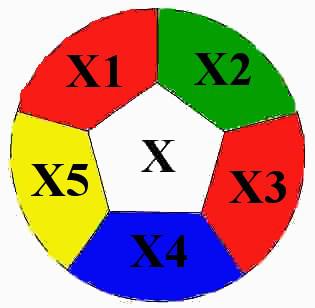
Se distinguen, de nuevo, dos posibilidades:
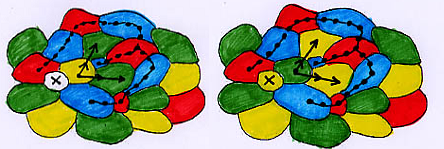
a) X2 no pertenece a la componente amarilla-verde de X5 o X2 no pertenece a la componente azul-verde de X4. En el primer caso (el otro se hace análogamente) se invierten el amarillo y el verde en esta componente y queda libre un color (en la figura 10, el amarillo) para X.
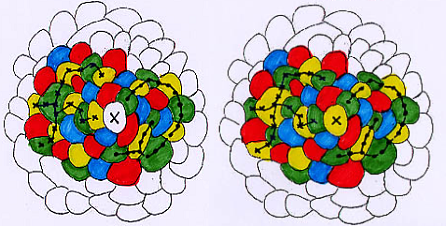
b) X2 pertenece a la componente amarilla-verde de X5 y X2 pertenece a la componente azul-verde de X4. Entonces, se invierten las componentes roja-azul de X1 y roja-amarilla de X3, para liberar el rojo para X.
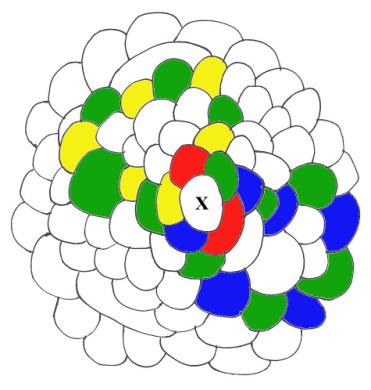
Así concluye la demostración de Kempe, prueba aceptada por la comunidad matemática, hasta 1890. En ese año, Percy John Heawood (1861-1955) publicó el artículo Map Colour Theorem en el Journal of Pure and Applied Maths: había encontrado –muy a su pesar– un mapa en el que la prueba de Kempe no funcionaba (ver figura 12).

En efecto, en la prueba dada por Kempe (caso v(X)=5, b) de la discusión anterior), las componentes amarilla-verde (y-g) de X5 y azul-verde (b-g) de X4 pueden cruzarse. Y entonces, las componentes rojo-azul (r-b) de X1 y rojo-amarillo (r-y) de X3 no pueden invertirse simultáneamente…
Kempe admitió su error en los Proceedings of the London Mathematical Society, y el 9 de abril de 1891, en un encuentro de la citada sociedad afirmó: “My proof consisted of a method by which any map can be coloured with four colours. Mr. Heawood gives a case in which the method fails, and thus shows the proof to be erroneous. I have not succeded in remedying the defect, though it can be shown that the map which Mr. Heawood gives can be coloured with four colours, and thus his criticism applied to my proof only and not to the theorem itself”.
A pesar de este error, Heawood usó el argumento de las cadenas de Kempe para probar el teorema de los 5 colores. Demostró también el llamado problema de coloreado de mapas de Heawood que acota superiormente el número de colores necesarios para colorear un mapa dibujado sobre una superficie sin borde, exceptuando el caso de la esfera (ver [3]).
En 1968, Gerhard Ringel y Ted Youngs (ver [3]) probaron que el problema de coloreado de mapas de Heawood daba el número exacto de colores para toda superficie, excepto la botella de Klein. En 1986, Thomas L. Saaty (ver [4]) demostró que para colorear un mapa sobre la botella de Klein se necesitan como mucho 6 colores.
¡Sólo quedaba por resolver el caso de mapas esféricos (equivalentemente, el de mapas planos)!
Conoceremos la solución en El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
Referencias
[1]Marta Macho Stadler, El teorema de los cuatro colores (1): una historia que comienza en 1852, Cuaderno de Cultura Científica, 26 abril 2017
[2] Marta Macho Stadler, Mapas, colores y números, Descubrir las matemáticas hoy: Sociedad, Ciencia, Tecnología y Matemáticas 2006 (2008) 41-68
[3] Robin Wilson, Four colors suffice: how the map problem was solved, Princeton University Press, 2002.
[4] J.L. Saaty, P.C. Kainen, The four colour problem: assaults and conquest, Dover, 1986.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
