Continuamos con la historia del teorema de los cuatro colores (ver [1] y [2]) cambiando de enfoque: existe una manera dual de abordar este problema, sustituyendo los mapas por grafos. ¿Cómo? Se marca la capital de cada país en el mapa, se unen las capitales de países contiguos y se obtiene el grafo dual del mapa. Colorear el mapa equivale a pintar las capitales (vértices del grafo), asignando distintos tonos a dos capitales unidas por una trayectoria (arista).

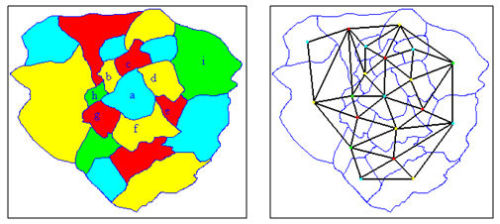
Puede demostrarse que los grafos duales de mapas son siempre planares, es decir, se puede dibujar en el plano una representación concreta del grafo, en la cual las aristas no se cortan excepto en un eventual vértice común (imagen 2).

Además, se puede probar que:

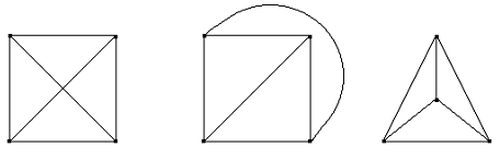
1. un mapa es cúbico (ver [1]) si y sólo si su grafo dual es triangular (grafo planar en el que cada cara tiene exactamente tres aristas),

2. el número de regiones colindantes coincide con el grado de cada vértice (número de aristas incidentes), y

3. los grafos duales heredan la fórmula de Euler:

Núm(vértices) – Núm(aristas) + Núm(caras) = 2

Imaginemos por un momento que el teorema fuera falso, es decir, que existen mapas (grafos) que no pueden 4-colorearse. Entre estos mapas (grafos) que necesitan cinco colores o más, debe de haber alguno con el menor número posible de regiones: es un minimal criminal. Así, un minimal criminal no puede 4-colorearse, pero un mapa (grafo) con menos regiones (vértices) sí.

Probar el teorema de los cuatro colores equivale a demostrar que no existen minimales criminales. De hecho, lo que Kempe demostró con su método de cadenas es que un minimal criminal no puede contener digones, triángulos o cuadrados (ver [2], figura 3), y cometió un error al intentar probar que tampoco puede contener pentágonos. Si hubiese conseguido esto último, habría quedado demostrado el teorema.

Los siguientes conceptos sobre grafos son fundamentales en la demostración del teorema:

1. una configuración es un ciclo con vértices internos triangulados;

2. un conjunto inevitable K es una familia finita de configuraciones tal que todo grafo contiene una copia conforme de una de K;

3. k es una configuración reducible, si se puede deducir el coloreado de cualquier grafo que contenga a k, a partir de un grafo menor.

La demostración del teorema de los cuatro colores copia la prueba de Kempe, pero para la inducción, en vez de eliminar un único vértice, se recorta una configuración.

El plan de la prueba consiste en encontrar conjuntos inevitables K; si K estuviese formado sólo por configuraciones reducibles, la demostración del teorema de los cuatro colores estaría terminada, ya que en tal caso no podría existir un minimal criminal.

En 1969, Heinrich Heesch sistematiza la prueba de la reducibilidad, desarrollando un algoritmo que intenta implementar en un ordenador. Realiza diversas pruebas en una máquina CDC1604A y entra en contacto con su alumno Wolfgang Haken (en EE. UU.), comentándole que la demostración necesita estudiar solamente 8.900 configuraciones.

A través de su algoritmo de descarga propone un método de construcción de conjuntos inevitables: Heesch considera el grafo como una red eléctrica; asociando a cada vértice una carga inicial de 6-d(v) (d(v) es el grado del vértice v).Usando la fórmula de Euler, demuestra que la suma de las cargas en un grafo triangulado es 12.

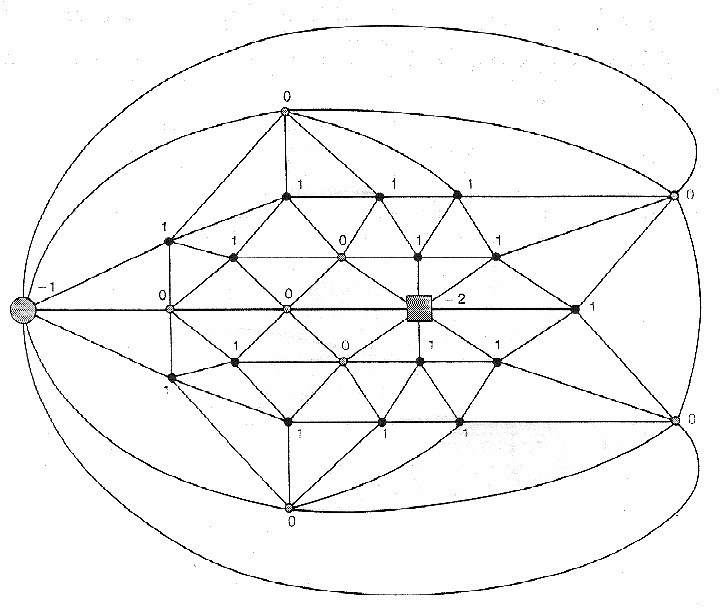
Desplazando las cargas eléctricas sobre la red (con su algoritmo de descarga), la suma total no varía: los vértices cargados positivamente pueden ceder cargas, los cargados negativamente pueden recibir y los de carga nula no intercambian. Con este sistema, su objetivo es eliminar de esta red eléctrica los vértices de carga negativa, obteniendo un conjunto de configuraciones con vértices de cargas positivas o nulas. Y como todo grafo triangulado es de carga total 12, debe contener al menos una de las configuraciones (cuya geometría dependerá del proceso de descarga elegido) del anterior conjunto, que forma entonces un conjunto inevitable.

Una vez obtenida la extensa lista de configuraciones inevitables, probando su reducibilidad, se tendría una prueba inductiva del teorema.

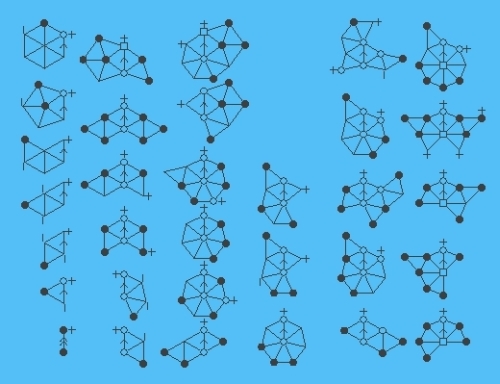
En 1976, Ken Appel y Wolfgang Haken dan una prueba cuyos principales ingredientes son precisamente los conceptos de reducibilidad y descarga.

La primera prueba de Appel, Haken y John A. Koch usa un algoritmo de descarga muy sofisticado, que produce una lista de 1.936 configuraciones inevitables, cada una de las cuales se demuestra reducible con la ayuda de un ordenador. Modificando consecutivamente el algoritmo de descarga, encuentran otro (con 300 reglas de descarga) produciendo 1.482 configuraciones inevitables, comprobando su reducibilidad mediante un ordenador programado por Koch: necesita 1.200 horas de cálculo en unIBM 360. Appel y Haken completan la demostración en 1976, tras seis años de duro trabajo: más de 100 páginas impresas, 400 microfilms con dibujos y la verificación de varios miles de casos particulares.

Todo este trabajo precisaba (en 1976) más de cincuenta días de trabajo en los tres ordenadores de la Universidad de Illinois, con un programa de varios miles de líneas… es decir, nadie podía comprobar la veracidad o falsedad del teorema a mano.

La hazaña de estos investigadores mereció un triunfal matasellos en 1977:

Appel y Haken reconocieron el papel fundamental de Kempe: Kempe’s argument was extremely clever, and although his “proof” turned out not to be complete, it contained most of the basic ideas that eventually led to the correct proof one century later.

Muchos matemáticos aceptan esta prueba como irrefutable, pero muchos otros argumentan que no se trata de una demostración matemática: la máquina había verificado que una enorme cantidad de mapas podían colorearse usando como mucho cuatro colores, pero, ¿y si existía un mapa que el ordenador no hubiese contemplado?

En 1996, un grupo de investigadores del Instituto de Tecnología de Georgia publicael artículo [6] en el que:

1. reducen las complicaciones, probando que la inevitabilidad de un conjunto reducible puede demostrarse con menos ejemplos que en la prueba de Appel y Haken;

2. su conjunto inevitable es solo de tamaño 633;

3. usan únicamente32 reglas de descarga;

4. la comprobación a mano de la inevitabilidad se reemplaza por una prueba formal verificable con un ordenador;

5. la verificación necesita únicamente tres horas en cualquier ordenador doméstico.

Posteriores investigaciones han ido confirmando cada una de las etapas de esta última prueba utilizando diferentes programas y métodos. Pero…El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?

Referencias

[1] Marta Macho Stadler, El teorema de los cuatro colores (1): una historia que comienza en 1852, Cuaderno de Cultura Científica, 26 abril 2017

[1] Marta Macho Stadler, El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba, Cuaderno de Cultura Científica, 10 mayo 2017

[3] Marta Macho Stadler, Mapas, colores y números, Descubrir las matemáticas hoy: Sociedad, Ciencia, Tecnología y Matemáticas 2006 (2008) 41-68

[4]K. Appel, W. Haken, Every planar map is four colourable, Part I: discharging, Illinois Journal of Mathematics 21, 429-490, 1977.

[5]K. Appel, W. Haken, J. Koch, Every planar map is four colourable, Part II: reducibility, Illinois Journal of Mathematics 21, 491-567, 1977.

[6]N. Robertson, D.P. Sanders, P. Seymour, R. Thomas, A new proof of the four-colour theorem, Electronic Announcements of the AMS 2, 17-25, 1996.

[7]R.J. Wilson, Four colors suffice: how the map problem was solved, Princeton University Press, 2002.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

Esta entrada participa en la Edición 8.4 “Matemáticas de todos y para todos” del Carnaval de Matemáticas cuyo anfitrión es, en esta ocasión, matematicascercanas.