Wolfgang Haken

Smote the Kraken

One! Two! Three! Four!

Quoth he: “the monster is no more”.

(W.T. Tutte)

El teorema de los cuatro colores se enunció en forma de conjetura en 1852, pero tuvo que esperar hasta el año 1996 para ser admitido como válido por la práctica totalidad de la comunidad matemática.

El poema que abre este escrito es precisamente el que William Thomas Tutte dedicó a Wolfgang Haken –uno de los investigadores que dio una primera prueba del teorema en 1977, aunque tuvo que esperar hasta 1996 a ser ratificada por otros investigadores– tras más de cien años de fallidos intentos por probar su validez.

El teorema de los cuatro colores afirma que, para colorear un mapa geográfico plano sin que dos países colindantes tengan el mismo color, basta con cuatro tonos diferentes.

Se imponen las siguientes restricciones a los mapas aludidos en el teorema:

1. son siempre conexos –es decir, de una pieza– y cada una de sus regiones también es conexa;

2. dos territorios distintos de un mapa no pueden tocarse sólo en un punto, es decir, para ser colindantes deben compartir frontera en el sentido indicado en la figura 1.

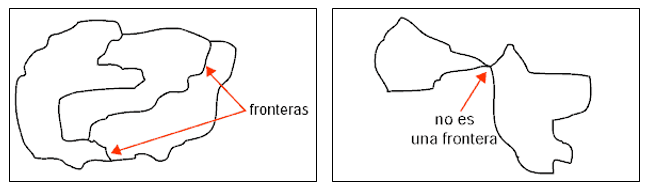
Podría pensarse que un mapa con una gran cantidad regiones, poseyendo extrañas formas, y colindando de manera singular necesitaría mayor cantidad de colores que un mapa más sencillo. Pero, el teorema afirma que no es el caso.

Se trata de un problema topológico, ya que no es importante la forma de las regiones del mapa, sino la manera en la están colocadas las unas respecto a las otras.

¿Cómo empezó esta historia? El abogado y botánico Francis Guthrie observó que era capaz de colorear un mapa complicado de los cantones de Inglaterra con sólo cuatro colores, y conjeturó que debía suceder lo mismo con cualquier otro mapa geopolítico. En 1852, se lo comentó a su hermano Frederick y éste a su vez a Augustus de Morgan, su profesor.

Francis Guthrie observó, además, que tres colores no bastaban, mostrando lo que llamó el diagrama crítico (figura 2), que obviamente precisa de cuatro colores para no contradecir las condiciones de su conjetura –la parte blanca central es una región del mapa–.

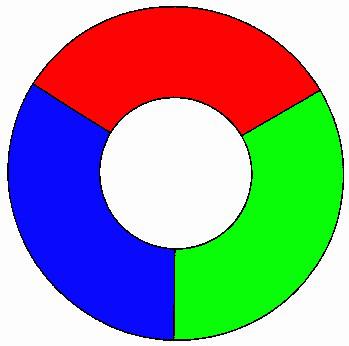
Frederick Guthrie fue el primero en observar que el problema de los cuatro colores no se podía generalizar a dimensión 3: en efecto, según un ejemplo posterior de Heinrich Tietze, es posible construir un ejemplo de mapa tridimensional que precise tantos colores como se desee. Su propuesta consistía en tomar barras numeradas de 1 hasta n,ordenándolas como muestra la figura 3, y sobre ellas colocaba otras n barras numeradas de 1 hasta n, girándolas 45 grados. De este modo, Tietze conseguía un mapa tridimensional conn regiones (cada número correspondía a un ‘país’), que obviamente necesitaba exactamente n colores para no contradecir las reglas de la conjetura…

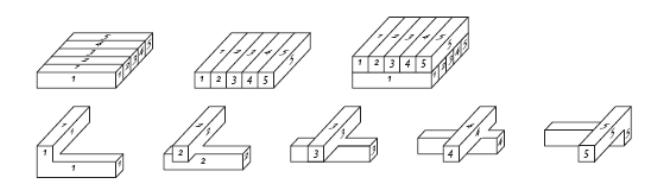
Augustus de Morgan se interesó por la conjetura de Guthrie y la difundió entre sus colegas. El 23 de octubre de 1852 escribió a William Rowan Hamilton: “A student of mine [se refiere a Frederick Guthrie] asked me today to give him a reason for a fact which I did not know was a fact – and do not yet. He says that if a figure be any how divided and the compartments differently coloured so that figures with any portion of common boundary line are differently coloured – four colours may be wanted, but not more – the following is the case in which four colours are wanted. Query cannot a necessity for five or more be invented […]”

En ese momento Hamilton estaba trabajando en teoría de cuaterniones, y respondió cuatro días después a De Morgan, con sarcasmo: “I am not going to attemt your quaternion of colour very soon”.

Decepcionado, De Morgan se puso en contacto con otros matemáticos. En 1853, escribió a William Whewell, describiendo la conjetura como un axioma matemático.

El problema de los cuatro colores cruzó el Atlántico: Charles Sanders Peirce dio un seminario sobre la demostración, aunque nunca la escribió.

Tras la muerte de De Morgan en 1871, el problema de los cuatro colores pareció olvidarse; aunque Peirce seguía buscando su demostración, ninguno de los amigos británicos de De Morgan lo mencionaban.

Años más tarde, en junio de 1878, Arthur Cayley hizo la siguiente pregunta en un encuentro de la London Mathematical Society: “Has a solution been given of the statement that in colouring a map of a country, divided into counties, only four colours are required, so that no two adjacent counties should be painted in the same colour”?.

Realmente interesado por el problema, en 1879 publicó una nota corta sobre el tema en los Proceedings of the Royal Geographical Society. Admitía la dificultad del tema: “I have not succeeded in obtaining a general proof: and it is worth while to explain wherein the difficulty consists”.

Entre otros, en esa nota observaba que, a la hora de probar el teorema, podían imponerse condiciones más restrictivas sobre los mapas a colorear, en particular, bastaba con limitarse a mapas cúbicos, es decir, aquellos en los que hay exactamente tres regiones en cada punto de encuentro. En efecto, si en un mapa hay más de tres regiones en alguno de los puntos de encuentro (ver figura 5); sobre este punto puede pegarse un pequeño parche que produce un mapa cúbico. Si se puede colorear este mapa con cuatro colores, también se puede obtener un 4-coloreado del mapa original: basta con colapsar el parche en un punto.

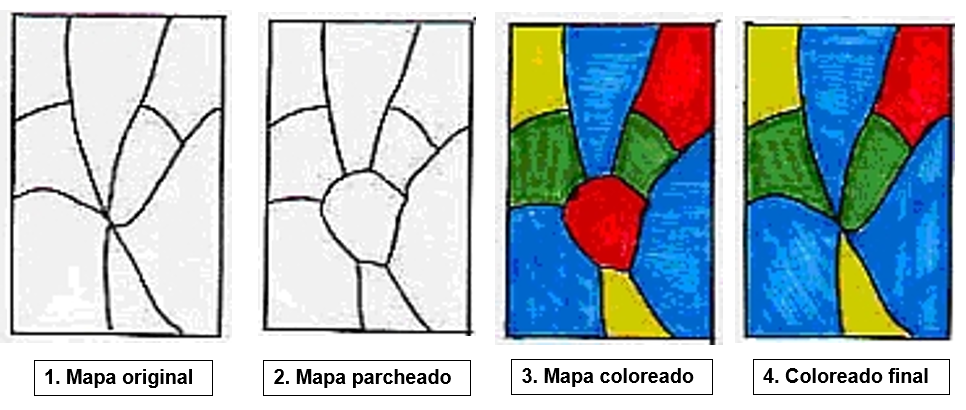
Continuará en… El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba.

Referencias:

Marta Macho Stadler, Mapas, colores y números, Descubrir las matemáticas hoy: Sociedad, Ciencia, Tecnología y Matemáticas 2006 (2008) 41-68

Robin Wilson, Four colors suffice: how the map problem was solved, Princeton University Press, 2002.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.