El teorema de Marion es un bonito ejemplo de resultado de geometría afín. No se sabe quién fue la primera persona que lo enunció, pero la matemática Marion Walter (1928) lo explicó en alguna de sus clases y también aparece en varios sus trabajos; por ello se recuerda con su nombre.
El teorema afirma lo siguiente:
Tomemos un triángulo cualquiera ABC, trisequemos sus lados y unamos cada uno de los dos puntos que definen esta división con el vértice del lado opuesto del triángulo (ver la figura 1). Queda determinada una región hexagonal central (de vértices DEFGHI en la figura 1) cuya área es 1/10 del área del triángulo original.
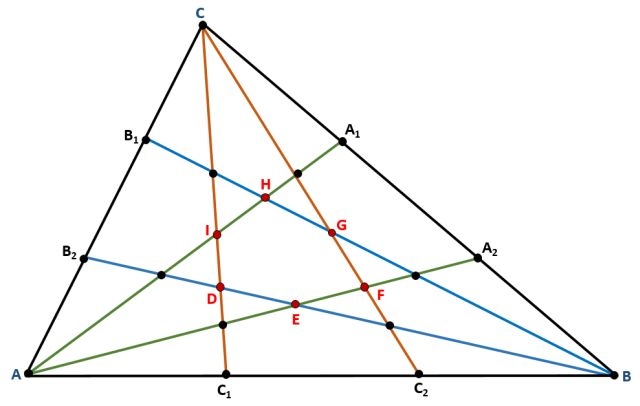
La demostración de este teorema no es complicada; puede encontrarse, por ejemplo, una prueba en [1] en la que se utilizan coordenadas trilineales respecto del triángulo ABC.
En 1994, Ryan Morgan (ver [2]) generalizó este teorema en los siguientes términos:
Dado un triángulo cualquiera ABC, si se dividen sus lados en n partes iguales (donde n es un número entero impar) y se une cada uno de los n-1 puntos que definen esta división con el vértice del lado opuesto del triángulo, entonces queda determinada una pequeña región hexagonal central. La razón entre el área de este hexágono y la del triángulo original es constante. Más concretamente, el área de esta región es
del área del triángulo original.
Para n=3 tenemos, efectivamente, el teorema de Marion.
Si n es par, el proceso anteriormente descrito no produce un hexágono central necesariamente, o no tiene porqué ser único. Aunque existen resultados parciales como el dado en [3] para n=4.
Recordemos que se llaman números poligonales centrados a aquellos números figurados que pueden representarse mediante un conjunto de puntos equidistantes formando un polígono regular. Entre ellos, los números nonagonales centrados son aquellos que pueden representarse sobre un nonánogo, con un punto en el centro rodeado de sucesivas capas nonagonales:
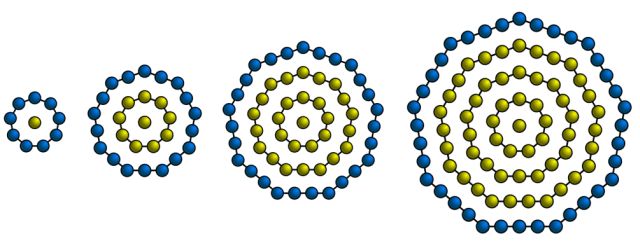
Los números (3n+1)(3n-1)/8, para n entero impar, que aparecen en el teorema de Morgan son precisamente números nonagonales centrados. Puede encontrarse un listado con los primeros y algunas de sus propiedades en The On-Line Encyclopedia of Integer Sequences (ver [4]); son: 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, 1081, 1225, 1378, 1540, 1711, 1891, 2080, 2278, 2485, 2701, 2926, 3160, 3403, 3655, 3916, 4186, 4465, 4753, 5050, 5356, 5671, 5995, 6328, 6670, 7021, 7381, 7750, 8128, 8515, 8911, 9316, …
¿No es emocionante ver como se relacionan estos números –los del teorema de Morgan y los nonagonales centrados–procedentes de acercamientos diferentes?
Por cierto, aparte de este bellísimo teorema, otra de las aportaciones que debemos a Marion Walter es una colección de setenta fotografías de su colección particular realizadas, en su mayoría, por la propia Marion y que han pasado a formar parte de los Archives of American Mathematics. En ellas aparecen notables matemáticas y matemáticos, comoTobias Danzig, Paul Erdös, Paul Halmos, Irving Kaplansky, Alexander Ostrowski, George Pólya, Mina Rees, Isaac Schoenberg u Olga Taussky-Todd, entre otros.
Referencias
[1] Marion’s theorem, Wolfram MathWorld
[2] Ryan Morgan, No Restriction Needed. The Mathematics Teacher 87, 726 y 743, 1994.
[3] Luca Goldoni, A generalization of Marions Walter’s theorem, 2016
[4] A060544: Centered 9-gonal, OEIS
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
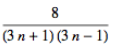

El grafo de Marion (Gray) — Cuaderno de Cultura Científica
[…] casi dos años hablamos en este Cuaderno de Cultura Científica del teorema de Marion (Walter), un bonito enunciado de geometría afín, nombrado en honor a la matemática Marion Walter –que […]
El grafo de Marion (Gray) – Fluceando
[…] casi dos años hablamos en este Cuaderno de Cultura Científica del teorema de Marion (Walter), un bonito enunciado de geometría afín, nombrado en honor a la matemática Marion Walter –que […]
Teoremas geométricos sin palabras: Viviani — Cuaderno de Cultura Científica
[…] Una pequeña joya geométrica: el teorema de van Aubel), el teorema de Marion (véase la entrada El teorema de Marion (Walter)), el teorema de la bandera británica (véase la entrada El teorema de la ikurriña), el teorema de […]