Como ya hemos comentado en anteriores entradas del Cuaderno de Cultura Científica, la geometría plana está repleta de interesantes y atractivos teoremas, que suelen venir acompañados de diagramas con mucho encanto, como el teorema de Napoleón (véase la entrada Variaciones artísticas del teorema de Napoleón), el teorema de van Aubel (véase la entrada Una pequeña joya geométrica: el teorema de van Aubel), el teorema de Marion (véase la entrada El teorema de Marion (Walter)), el teorema de la bandera británica (véase la entrada El teorema de la ikurriña), el teorema de Pick (véase la entrada Calcular el área contando puntos) o el mismísimo teorema de Pitágoras (véase la entrada Pitágoras sin palabras).

Estos resultados geométricos suelen tener diferentes tipos de demostraciones, en función de las técnicas utilizadas, la originalidad de las ideas contenidas, la complejidad de la misma o la extensión que ocupa. Lo más importante a la hora de demostrar un resultado matemático es obtener una demostración para el mismo, no importa lo larga, “poco elegante” o “aburrida” que nos pueda parecer, después ya podrán obtenerse demostraciones más originales, sugerentes, “hermosas”, simples o cortas. En esta búsqueda de la belleza en las demostraciones matemáticas también juegan un papel interesante las llamadas “demostraciones sin palabras”.

En 1973, el gran divulgador de las matemáticas Martin Gardner (1914-2010), se refirió a las demostraciones sin palabras como diagramas “en un vistazo” y señaló que “en muchos casos, una demostración farragosa puede ser suplida por una geométrica análoga, tan simple y bella que la veracidad de un teorema es casi vista en una ojeada”. Como comenta el matemático Roger B. Nelsen, una de las personas que más ha hecho por la difusión de las demostraciones sin palabras y autor de la serie de libros Proofs without Words (MAA), las demostraciones sin palabras no son realmente demostraciones matemáticas en sí mismas, son más bien diagramas, esquemas o dibujos que nos ayudan a comprender por qué un teorema es cierto o que encierran la idea de la verdadera demostración matemática. Son sugerentes, atractivas y todo un ejercicio de estímulo del pensamiento.

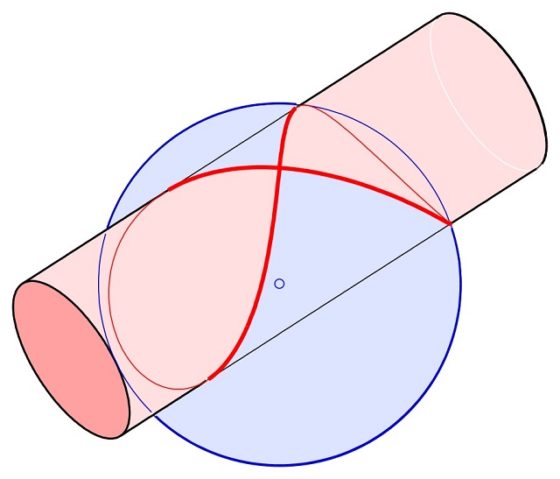
Con esta entrada iniciamos una pequeña serie estival de demostraciones sin palabras de interesantes y hermosos teoremas geométricos. Esta primera entrada de la serie está dedicada a un teorema clásico de la geometría del plano sobre triángulos equiláteros, el conocido teorema de Viviani. Este resultado geométrico debe su nombre al matemático italiano Vincenzo Viviani (1622-1703), que fue discípulo de Galileo Galilei (1564-1642) y Evangelista Torricelli (1608-1647) y que muchos conocemos por la llamada curva de Viviani, que es la curva intersección de un cilindro y una esfera.

Pero vayamos con el resultado geométrico anunciado, el teorema de Viviani.

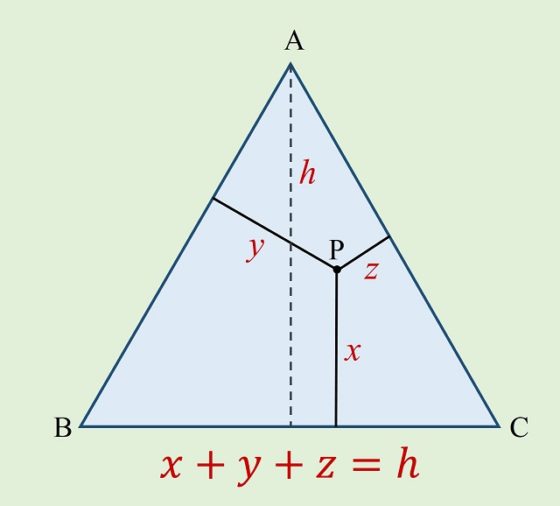
Teorema de Viviani: La suma de las distancias de un punto cualquiera en el interior de un triángulo equilátero (o en alguno de sus lados) a cada uno de sus lados es igual a la altura del mismo.

Este es un resultado geométrico que es fácil de probar, sin más que utilizar que el área de un triángulo es la mitad del producto de la base por la altura: área triángulo = (base x altura ) / 2.
La demostración sería la siguiente: el triángulo equilátero ABC (de base BC y altura h) puede descomponerse como unión de los tres triángulos PBC (de base BC y altura x), PAB (de base AB y altura y) y PCA (de base CA y altura z). Tomando áreas para los cuatro triángulos,

área (ABC) = área (PBC) + área (PAB) + área (PCA),

y teniendo en cuenta que los lados del triángulo equilátero ABC son iguales AB = BC = CA (a cuya longitud llamaremos l), se tiene que

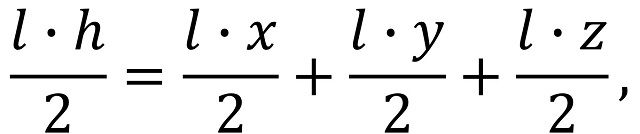
de donde se obtiene la igualdad deseada

En el libro Proofs without words, de Roger B. Nelsen, se recoge una primera demostración sin palabras del teorema de Viviani, publicada por Samuel Wolf en Mathematics Magazine, en 1989.

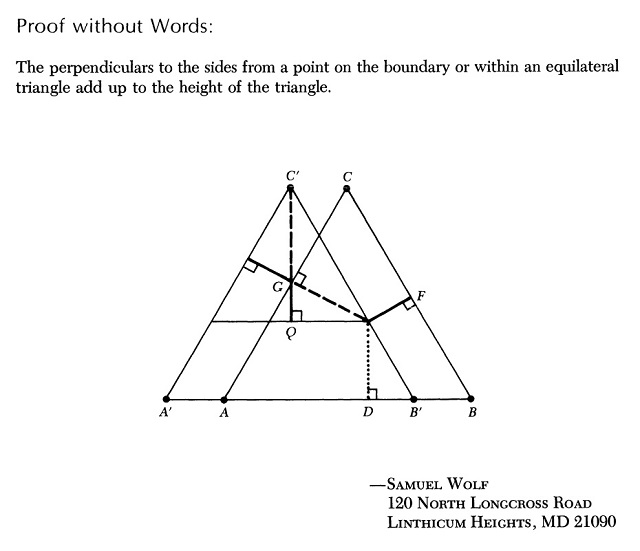
Expliquemos el motivo por el cual este esquema explicaría el teorema de Viviani. Para dar la explicación hemos llamado P_A, P_B y P_C a las proyecciones (ortogonales) del punto P sobre los lados BC, CA y AB (es decir, PP_A = x, PP_B = z, PP_C = y, de forma que el teorema establece que la altura h es igual a PP_A + PP_B + PP_C), como se muestra en la imagen siguiente. En primer lugar, se realiza una copia desplazada A’B’C’ del triángulo equilátero ABC, de forma que el punto P quede en el lado A’C’, y denotamos por Q la proyección (ortogonal) de A’ sobre la recta RP, paralela a BC, y L a la proyección (ortogonal) de P sobre la recta A’B’.

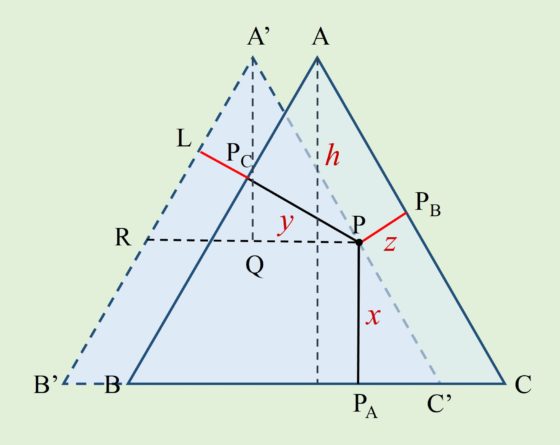
Entonces, tenemos las siguientes igualdades:

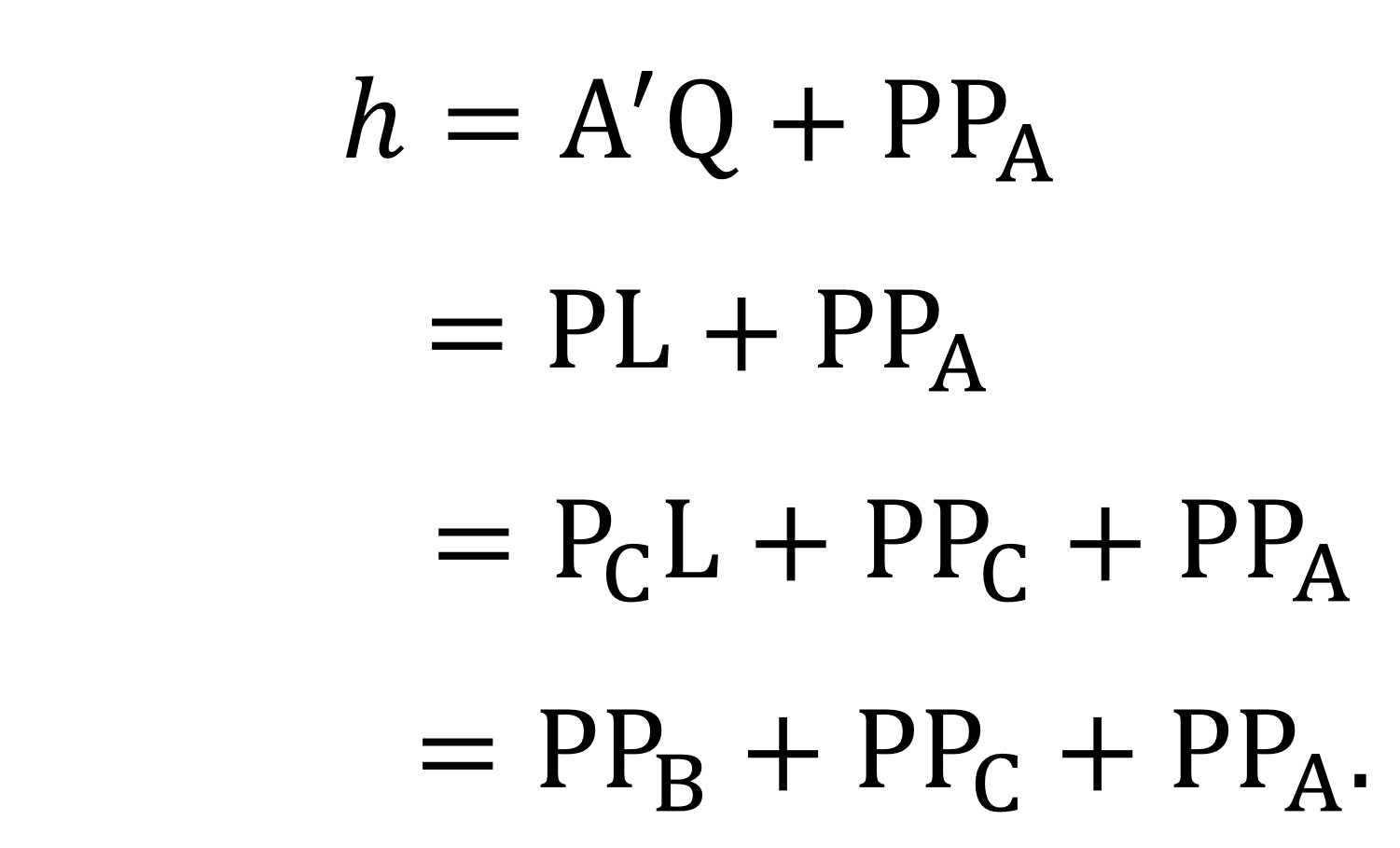
Luego el diagrama anterior es una demostración sin palabras del teorema de Viviani.

La segunda demostración sin palabras del teorema de Viviani la descubrí en el hermoso libro Charming Proofs, A Journey Into Elegant Mathematics de Claudi Alsina y Roger B. Nelsen. Es una demostración sin palabras de una gran sencillez y belleza, que publicó el matemático japonés Ken-ichiroh Kawasaki en Mathematics Magazine, en 2005.

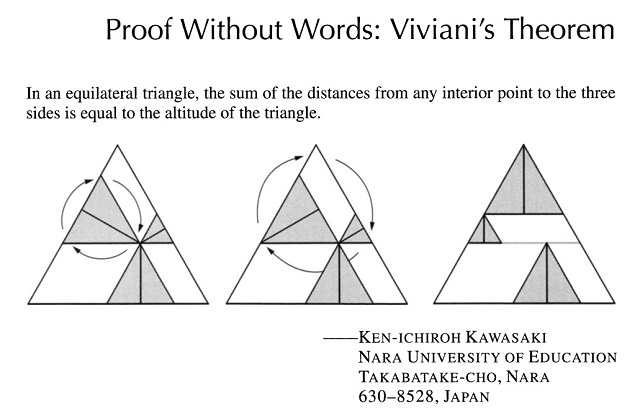
Es una hermosa demostración que se explica por sí sola.

Para terminar esta entrada estival del Cuaderno de Cultura Científica os dejo un problema que puede resolverse con una sencilla prueba sin palabras.

Problema (El cuadrado dentro del cuadrado): Demuéstrese que si se trazan rectas que unen los vértices del cuadrado con los puntos medios de uno de los lados opuestos, como se muestra en la siguiente imagen, entonces el área del cuadrado central es un quinto del área del cuadrado original.

Bibliografía:

1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, 1991.

2.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.

3.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.

4.- Tim Doyle, Lauren Kutler, Robin Miller, Albert Schueller, Proofs Without Words and Beyond, Convergence, MAA, 2014.

5.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica