En más de una ocasión hemos hablado en esta sección del Cuaderno de Cultura Científica, Matemoción, de la belleza de algunos resultados matemáticos y de sus demostraciones. En esta entrada vamos a centrar nuestra atención en uno de esos hermosos resultados matemáticos, en concreto, perteneciente al área de la geometría, el teorema de Pick, que permite calcular el área de una cierta región sin más que contar una serie de puntos.

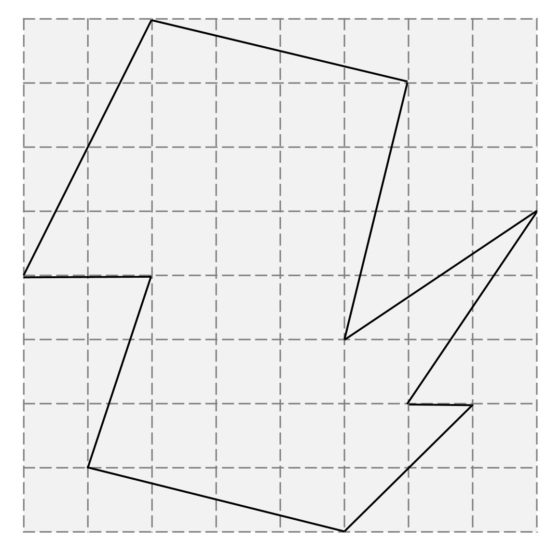
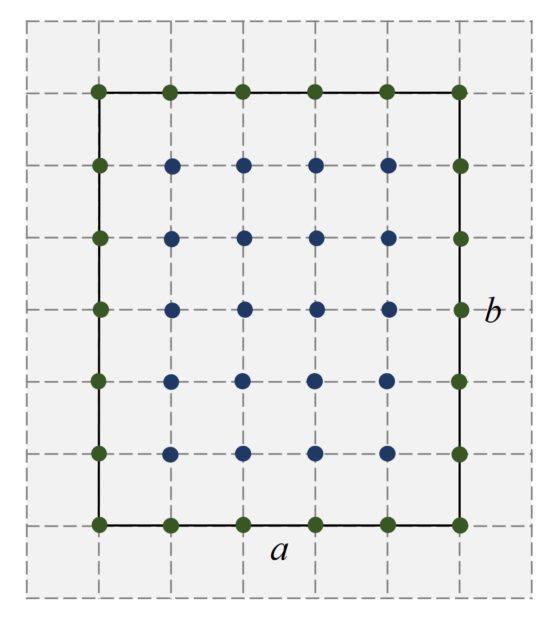
Imaginemos que queremos calcular el área de una región como la anterior. Un razonamiento rápido que podemos hacer es el siguiente. Contando los cuadrados de la retícula que están dentro de la región sabemos que su superficie va a ser mayor que el área de los 22 cuadrados interiores, es decir, mayor que 22 unidades cuadradas (si los cuadrados de la retícula son de un metro de lado, la región tendría más de 22 metros cuadrados), como se ve en la siguiente imagen.

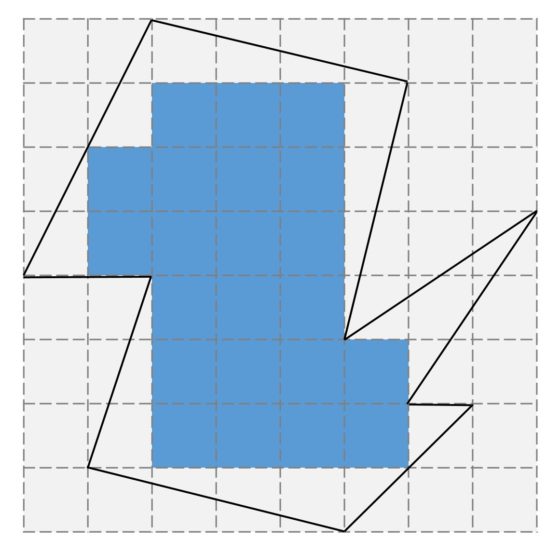
Por otra parte, contando los cuadrados de la retícula que encierran a nuestra región sabemos que la superficie de la misma va a ser menor que 48 unidades cuadradas.

Pero, ¿cuál es el área exacta de esa región? Lo curioso de la respuesta a esta cuestión es que se puede calcular simplemente contando puntos. Miremos a la siguiente imagen. En ella hemos pintado los puntos que son vértices del retículo (las intersecciones de las líneas horizontales y verticales) que están en la frontera de nuestra región (los puntos verdes, B = 13) y los puntos que están en el interior de la misma (los puntos azules, I = 29).

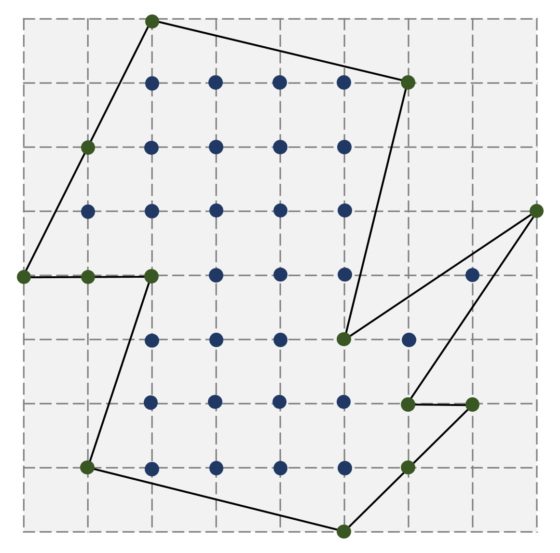
El resultado del que vamos a hablar en esta entrada, el teorema de Pick, nos dice que el área de esa región es igual a

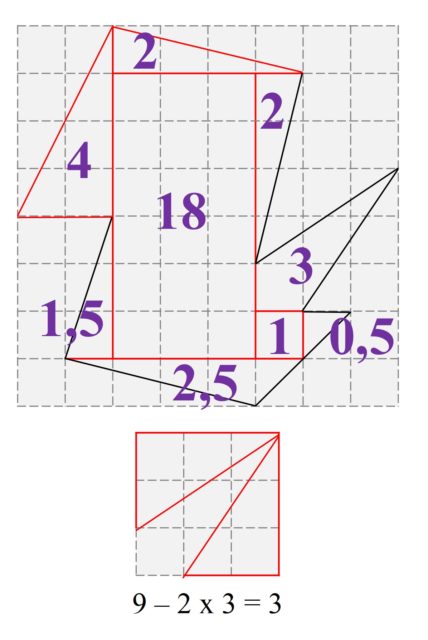
A = I + B/2 – 1 = 29 + 13/2 – 1 = 34,5 u.c.

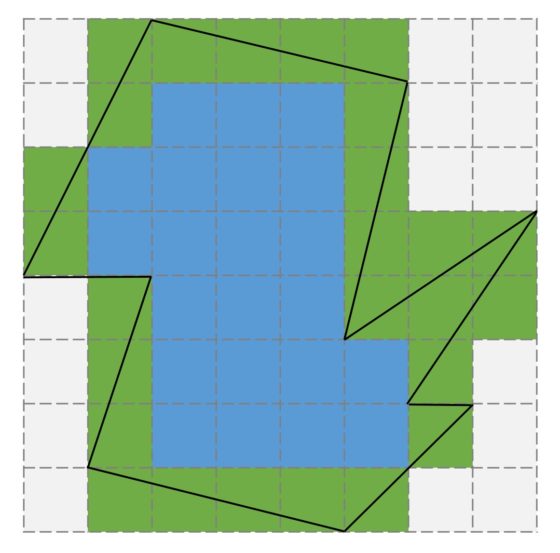
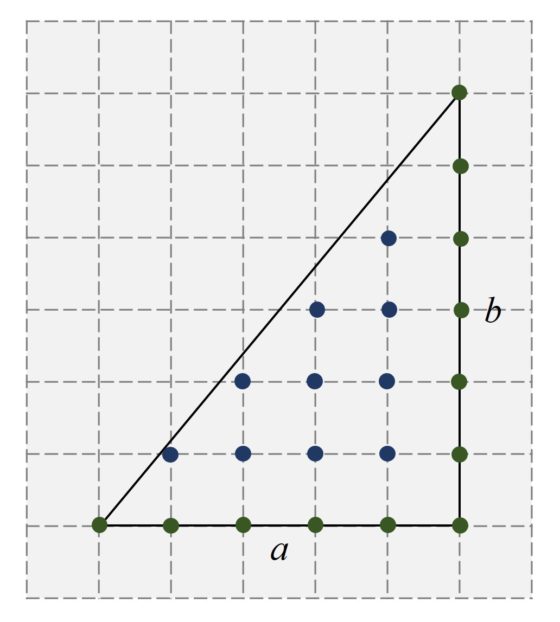
Veamos, con un poco de geometría básica, es decir, utilizando simplemente que el área de un rectángulo es base por altura y que la de un triángulo es base por altura dividido entre dos, que es así. Como vemos en la siguiente imagen, en la que se ha descompuesto la región en rectángulos y triángulos, el área es efectivamente 34,5 unidades cuadradas.

Pero vayamos con el teorema de Pick. Este bello y curioso resultado geométrico se debe al matemático austriaco Georg Alexander Pick (1859-1942) –matemático judío que introdujo a Albert Einstein en la geometría del cálculo tensorial que este necesitaba para la teoría de la relatividad y que murió en el campo de concentración de Theresienstadt– quien lo publicó en 1899 en la revista Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen «Lotos» in Prag. (Neue Folge) bajo el título Geometrisches zur Zahlenlehre (algo así como Resultados geométricos para la teoría de números). Aunque el resultado empezó a llamar la atención después de que fuese recogido en la edición de 1969, en inglés, del libro de divulgación matemática Mathematical Snapshots (publicado originalmente en polaco en 1938) del matemático polaco Hugo Steinhaus (1887-1972). Desde entonces se ha convertido en un resultado geométrico muy conocido, del que se han publicado diferentes demostraciones.

El teorema de Pick es sorprendente ya que nos permite calcular el área de una cierta región simplemente contando puntos, de la frontera y del interior, sin tener en cuenta otras cuestiones más directamente conectadas con la geometría de la región. El enunciado de este resultado es el siguiente.

Teorema de Pick: Sea P un polígono reticular y simple, entonces el área de la región encerrada por el polígono es igual a

A = I + B/2 – 1,

donde I son los puntos del retículo que están en el interior del polígono y B son los puntos del retículo que están en la frontera, es decir, en el polígono.

Antes de nada, vamos a explicar brevemente los conceptos que aparecen en este resultado. Un polígono reticular es un polígono trazado sobre una retícula, como en nuestro ejemplo, de forma que los vértices del polígono están sobre los vértices del retículo (como ya hemos comentado, los puntos intersección de las líneas horizontales y verticales de la retícula).

Por otra parte, un polígono reticular es simple si su frontera –los lados del polígono– no se intersecan entre sí. Para los polígonos reticulares no simples, como el del siguiente cuadrilátero de la imagen, no se verifica el resultado de Pick.

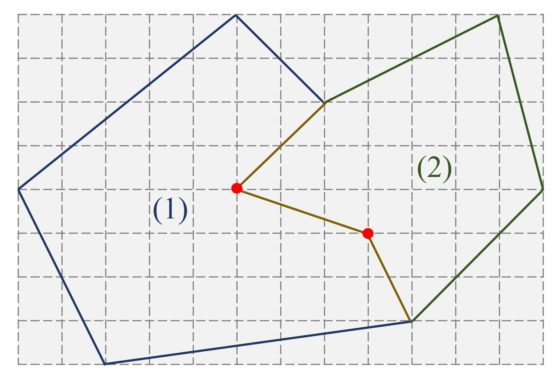
A continuación, veamos una idea de la demostración. El primer paso es observar que la fórmula del teorema de Pick, I + B/2 – 1, es aditiva, es decir, que si tenemos una región S cuya frontera es un polígono reticular simple y esta región es la unión de dos regiones más pequeñas –S es la unión de S₁ y S₂– cuyas fronteras son polinomios reticulares simples que verifican la fórmula de Pick, entonces también se verifica la fórmula para la región grande, unión de las regiones 1 y 2.

En la siguiente imagen tenemos un ejemplo de una región S que es unión de las regiones más pequeñas S₁ y S₂.

Además, hemos asumido que la fórmula del teorema de Pick se verifica para las regiones pequeñas S₁ y S₂,

A₁ = I₁ + B₁/2 – 1,

A₂ = I₂ + B₂/2 – 1,

veamos entonces que también se verifica para la región S, unión de las dos anteriores.

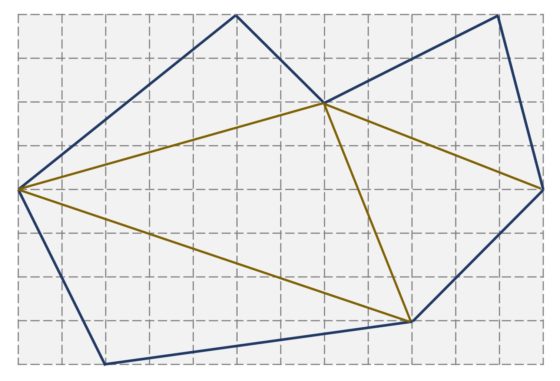
Para empezar, el conjunto de los puntos interiores de la región grande S está formado por los puntos interiores de las regiones pequeñas S₁ y S₂, más los puntos que están en la frontera poligonal común de las dos regiones S₁ y S₂, y que no están en la frontera poligonal de S (los puntos rojos de la imagen). Por lo tanto, la cantidad de puntos interiores de S es igual a

I = I₁ + I₂ + K,

donde K es la cantidad de esos puntos que están en la frontera poligonal común de las dos regiones S₁ y S₂, pero que no están en la frontera poligonal de S.

Respecto a los puntos que están en la frontera poligonal de la región S, son los puntos de la frontera poligonal de cada una de las dos S₁ y S₂, menos los K puntos que están en la frontera común. Aunque hay que tener cuidado de no contar dos veces los dos puntos que están en la frontera S₁ y S₂, pero también en la de S. Por lo tanto,

B = B₁ – K + B₂ – K – 2 = B₁ + B₂ – 2K – 2.

Ahora computemos la fórmula del teorema de Pick para la región S,

I + B/2 – 1 = (I₁ + I₂ + K) + (B₁ + B₂ – 2K – 2)/2 – 1,

que trivialmente es igual a

(I₁ + B₁/2 – 1) + (I₂ + B₂/2 – 1) = A₁ + A₂,

es decir, el área A de la región S.

El siguiente paso de la demostración para probar el teorema de Pick es que cada región cuya frontera es un polígono reticular simple se puede descomponer en triángulos (reticulares). Este resultado se puede probar por inducción sobre el número de vértices del polígono simple (considerando una diagonal interior del polígono).

Teniendo en cuenta los dos pasos anteriores, bastará probar que el teorema de Pick es verdadero para los triángulos reticulares, ya que si el resultado es cierto para los triángulos y todo polígono simple se puede dividir en triángulos, por la propiedad aditiva de la fórmula de Pick se concluye.

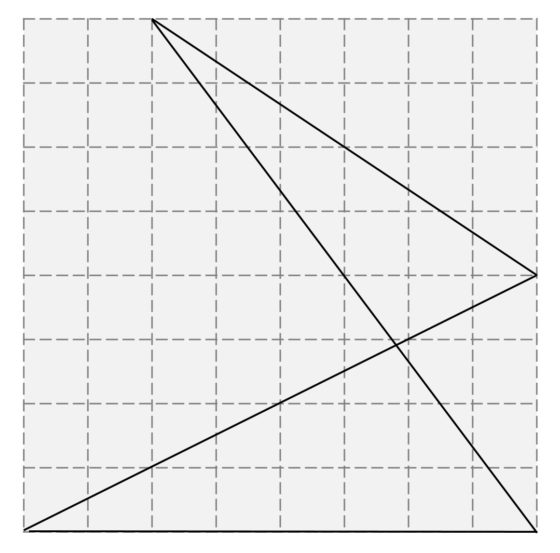
Veamos, por lo tanto, que la fórmula de Pick se cumple para los triángulos reticulares. Para empezar, consideremos un rectángulo, como el de la imagen, entonces la fórmula se cumple trivialmente. Si el rectángulo (reticular) tiene lados de longitudes a y b, entonces el número de puntos de la frontera es B = 4 + 2(a – 1) + 2(b – 1) = 2 (a + b) y el número de puntos del interior es I = (a – 1) x (b – 1) = ab – a – b + 1, luego

I + B/2 – 1 = ab,

el área A del rectángulo de lados a y b.

De aquí se va a deducir que también es verdad para triángulos rectángulos. Para lo cual se pueden considerar tres casos posibles: i) el cuadrado, ii) rectángulo con a y b son pares, y iii) rectángulo con al menos uno de los lados, a y b, impares. Por ejemplo, para este último caso, que es el que se corresponde con la siguiente imagen, se tiene que B = a + b + 1 e I = (ab – a – b + 1) / 2, para los que se comprueba que

I + B/2 – 1 = ab/2,

el área A del triángulo rectángulo de lados a y b.

Finalmente, habría que demostrar que la fórmula de Pick es válida para cualquier triángulo reticular. Para probarlo se empieza inscribiendo el triángulo en una zona rectangular, quedándonos una de las siguientes situaciones.

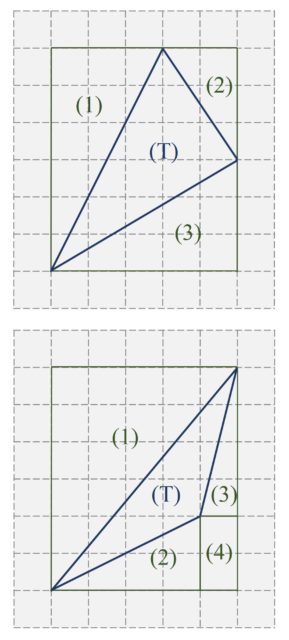
Ahora, que la fórmula de Pick se verifica para estos triángulos es una consecuencia de la propiedad aditiva de la fórmula y de que la misma se cumpla para los rectángulos y los triángulos rectángulos. Por ejemplo, para el primer caso, como la fórmula de Pick se cumple para el rectángulo en el que está inscrito nuestro triángulo, así como para los tres triángulos rectángulos de la imagen, entonces, por la propiedad aditiva de la fórmula de Pick, se tiene que cumplir también para la región que falta del rectángulo, que no es otra que la dada por nuestro triángulo inicial. Y de forma similar se actuaría para el segundo caso.

En consecuencia, ha quedado demostrado el teorema de Pick, puesto que toda región cuya frontera es un polígono reticular simple puede descomponerse en triángulos reticulares, para los cuales se cumple el teorema de Pick, deduciéndose el resultado para el polígono reticular inicial por la propiedad aditiva de la fórmula de Pick.

Existen varias demostraciones del teorema de Pick, algunas muy interesantes y hermosas, como las basadas en la fórmula de Euler o en el peso del polígono definido a través de los ángulos del mismo, pero de ellas ya hablaremos en otra ocasión.

Vamos a terminar esta entrada cuestionándonos si el resultado será cierto para el volumen de una región tridimensional similar, es decir, encerrada en un poliedro reticular. En 1957 el matemático británico John Reeve demostró, con el llamado tetraedro de Reeve, que no es posible un resultado análogo.

El tetratedro de Reeve es un tetraedro del espacio coordenado tridimensional cuyos vértices están en los puntos de coordenadas (0, 0, 0), (1, 0, 0), (0, 1, 0) y (0, 0, r), para r un número natural, como se muestra en la imagen (para r = 2, 3, 4).

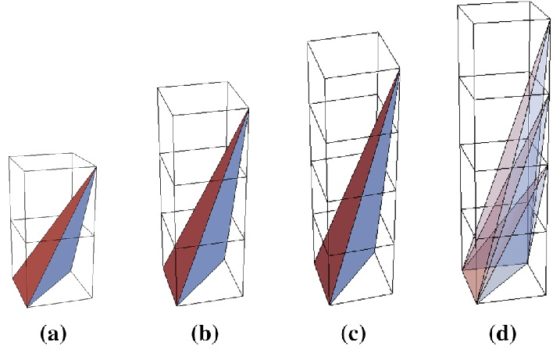
El volumen de estos tetraedros es r/6, es decir, varía con los diferentes valores de r. Sin embargo, todos estos tetraedros no tienen puntos interiores y tienen siempre cuatro puntos en su frontera, el tetraedro. Por lo tanto, no es posible un teorema de Pick ya que la cantidad de puntos interiores y frontera de esta familia de tetraedros reticulares no varía, pero sí el volumen de los mismos.

Bibliografía

1.- Martin Aigner, Günter M. Ziegler, El libro de las demostraciones, Nivola, 2005.

2.- Keith Ball, Strange Curves, Counting Rabbits and other Mathematical Explorations, Princeton University Press, 2003.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica