Hace unos años escribí una biografía sobre el matemático británico Arthur Cayley (1821-1895), que es uno de esos matemáticos por los que siento cierta admiración. Arthur Cayley investigó prácticamente en todas las áreas de las matemáticas –escribió 967 artículos y un libro sobre funciones elípticas–, en un tiempo en el que la investigación matemática era como una de esas expediciones geográficas, llenas de aventuras, del siglo XIX y principios del siglo XX, pero por territorio matemático. Escribiendo el libro Cayley, el origen del álgebra moderna aprendí algunas cosas sobre las particiones de los números naturales, tema al que vamos a dedicar esta entrada del Cuaderno de Cultura Científica.

Sin embargo, me gustaría empezar con un poco de literatura. En concreto, con una cita de la novela El contable hindú (Anagrama, 2011), del escritor estadounidense David Leavitt, novela que se centra en la relación de los matemáticos Srinivasa Ramanujan (1887-1920) y Godfrey H. Hardy (1877-1947), y en el ambiente de la Universidad de Cambridge de principios de siglo XX.
Por la mañana, va hasta las habitaciones de Hardy. Cuando se quita el abrigo, las lentejas se le caen del forro.
— ¿Le pasa algo? — pregunta Hardy— Parece agotado.
— Me pasé la noche cocinando. Voy a dar una cena. El martes que viene. Me pregunto si me haría el honor de asistir.
— Pues claro —dice Hardy—. ¿Qué se celebra?
— Que Chatterjee se va a casar. […]
— ¿Está seguro de que se encuentra bien? —pregunta Hardy. Ramanujan asiente con la cabeza.
— Se lo pregunto porque parece un poco distraído. ¿Es por la cena?
— Qué va. Son las lentejas.
— ¿Qué lentejas?
— Las del rasam. —Y Ramanujan se pone a explicarle que, mientras preparaba los ingredientes para el rasam, se dedicó a contar las lentejas, y eso le hizo pensar en las particiones.
No es la primera vez que hablan sobre las particiones. De hecho, tienen la teoría de las particiones en mente (aunque de un modo bastante disperso) desde que Hardy recibió la primera carta de Ramanujan y se topó con un enunciado sobre la serie theta cuya inexactitud permitía enfocar la cuestión desde un ángulo nuevo realmente sorprendente. Calcular p(n) —el número de particiones de un número— es fácil cuando n es 5 o 7; el problema es que, a medida que el número va siendo más alto, p(n) aumenta a un ritmo asombroso. Por ejemplo, el número de particiones de 7 es 15, mientras el número de particiones de 15 es 176. Así que ¿cuál es el número de particiones de 176? 476.715.857.290. Y entonces, ¿cuál sería el número de particiones de 476.715.857.290?
— ¿Y adónde le han llevado las lentejas?
— Tengo una idea sobre una fórmula para calcular el número de particiones de un número. Aunque sea un número muy alto. —Se levanta—. ¿Puedo?
—Claro. —Hardy borra la pizarra, y Ramanujan se acerca a ella. Empieza a trazar diagramas: puntitos que representan las lentejas. Luego escribe la serie theta de su primera carta. Entonces Hardy menciona la función generadora que descubrió Euler, y […].

Pero vayamos con las particiones. Una partición de un número natural es una forma de expresarlo como suma de números naturales, donde el orden no es relevante. Por ejemplo, el número 3 puede expresarse como suma de números naturales de tres formas distintas
1 + 1 + 1, 2 + 1, 3,
es decir, hay tres particiones del número 3, mientras que existen cinco particiones del número 4, a saber,
1 + 1 + 1+ 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4.
Dicho de una forma un poco más técnica, una partición de un número entero positivo n es una sucesión no creciente de números enteros
![]()
de forma que su suma es n,
![]()
Se denota por p(n) el número de particiones de un número n y por convención se toma p(0) = 1. Calcular las particiones de números pequeños es un problema sencillo, incluso un juego entretenido. Se puede ver fácilmente que p(6) = 11, p(7) = 15, p(8) = 22, p(9) = 30 y p(10) = 42. Sin embargo, la cuestión se complica según vamos avanzando en los números naturales. Por ejemplo, un número bajo como 100 tiene ya p(100) = 190.569.292 particiones, que no es precisamente un número pequeño. Solo en escribir explícitamente las particiones de 100 tardaríamos bastante más de 18 años y eso considerando que se estuviese escribiendo a un ritmo muy rápido y sin parar a descansar en todo el día, las 24 horas del día. O 36 años, a 12 horas diarias. Además, como se menciona en El contable hindú es una función que crece exponencialmente.
Por otra parte, se define como pk(n) el número de particiones del número n con k, o menos, sumandos. Por ejemplo, p3(6) = 7, ya que el 6 se puede expresar como suma de 3, o menos, sumandos de estas siete formas distintas
2 + 2 + 2, 3 + 2 + 1, 3 + 3, 4 + 1 + 1, 4 + 2, 5 + 1, 6.
Mientras que se denota por qk(n) al número de particiones del número n cuyos sumandos son menores, o iguales, a k. Por ejemplo, q3(6) = 7, ya que existen siete particiones del 6 cuyos sumandos son 1, 2 o 3,
1 + 1 + 1 + 1 + 1 + 1, 2 + 1 + 1 + 1 + 1, 2 + 2 + 1 + 1, 2 + 2 + 2, 3 + 1 + 1 + 1, 3 + 2 + 1, 3 + 3.
Se estudian muchos más tipos de particiones: con números impares, con números distintos, con determinado tipo de números, con solo ciertos números, planas, perfectas, etcétera. Además, si en las particiones se tuviera en cuenta el orden se obtendrían las composiciones o particiones ordenadas, pero hoy no vamos a hablar de estas.
La primera referencia a las particiones aparece en una carta, de 1669, del matemático alemán Gottfried Leibniz (1646-1716) al matemático suizo Johann Bernoulli (1667-1748), aunque las llama «divulsiones». Sin embargo, fue Leonhard Euler quien realizó el primer estudio serio de las particiones en su libro Introductio in analysin infinitorum (1748). Además de Euler, han estudiado las particiones de los números matemáticos como Arthur Cayley, James J. Sylvester (1814-1897), Percy A. MacMahon (1854-1929), Godfrey H. Hardy, Srinivasa Ramanujan y muchos más.

En el texto Introductio in analysin infinitorum, Leonhard Euler expresó la sucesión de los números de particiones {p(n)} como coeficientes de una función generatriz, una serie infinita de potencias. En concreto, demostró que
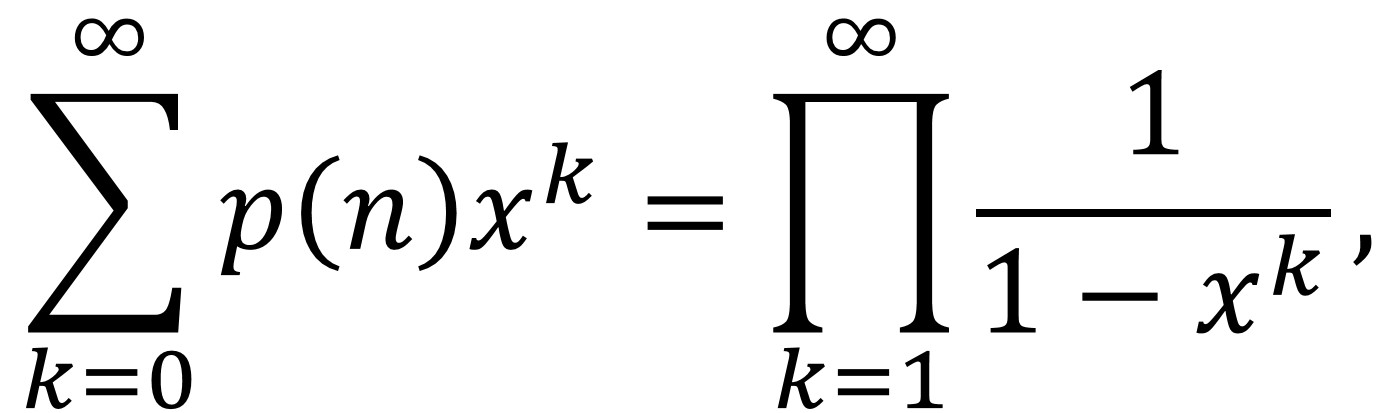
pero no vamos a explicar en esta entrada del Cuaderno de Cultura Científica el significado e importancia de esta potente fórmula matemática, sino que vamos a mostrar una técnica más visual de estudio de las particiones de los números, los denominados diagramas de Ferrers.
Norman Macleod Ferrers (1829-1903) fue un matemático británico de la Universidad de Cambridge, como muchos de los protagonistas del estudio de las particiones de los números. Un diagrama de Ferrers es un diagrama de puntos en el que cada partición se representa con una serie de puntos de forma que en cada fila haya tantos puntos como el número que se está sumando. Por ejemplo, la partición 21 = 6 + 4 + 4 + 2 + 2 + 2 + 1 se representa con una fila de seis puntos, dos de cuatro puntos, tres de dos puntos y una de un punto, como se ve en la siguiente imagen.

Si en el diagrama de Ferrers de una cierta partición se intercambian las filas por las columnas, se obtiene el diagrama de una nueva partición del mismo número, que es la denominada partición conjugada de la primera. Por ejemplo, si al diagrama de la imagen anterior, correspondiente a la partición 21 = 6 + 4 + 4 + 2 + 2 + 2 + 1, se le intercambian filas y columnas, se obtiene el diagrama de la partición conjugada de la anterior, la partición 21 = 7 + 6 + 3 + 3 + 1 + 1.
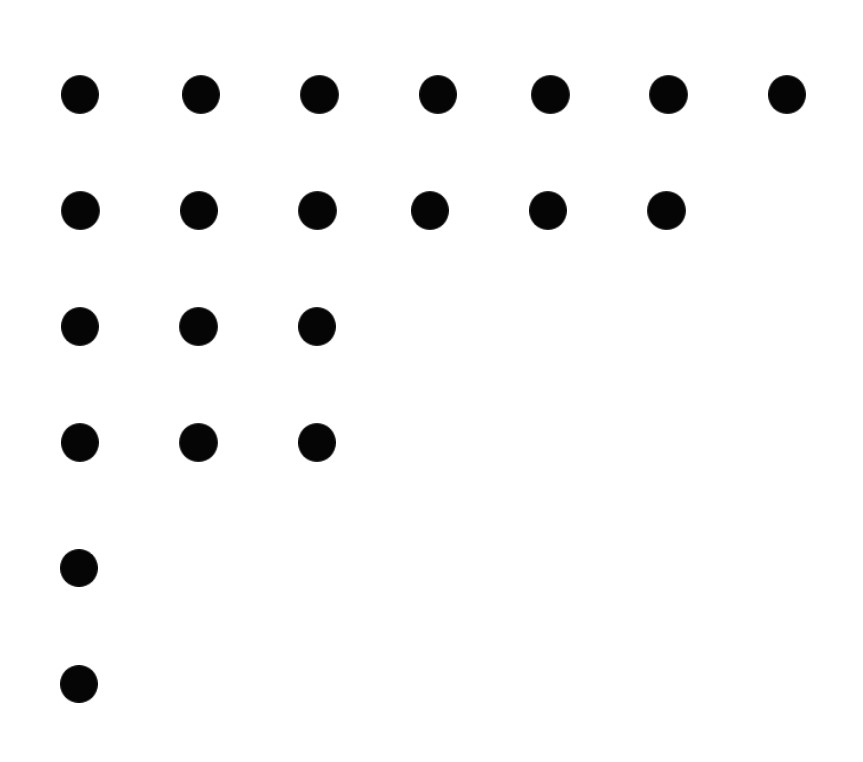
Observando los diagramas de Ferrers de particiones conjugadas se deduce que dada una partición de un número n con k, o menos, sumandos (el número de sumandos se corresponde con el número de filas, que no puede ser mayor que k), su partición conjugada es una partición de n donde los sumandos son números menores, o iguales, que k (puesto que ahora el número de puntos de cada columna no puede exceder k, que era la cantidad de filas que había antes). Y el recíproco también es cierto. Por ejemplo, en las imágenes anteriores, la partición 6 + 4 + 4 + 2 + 2 + 2 + 1, tiene siete o menos sumandos, y su conjugada, 7 + 6 + 3 + 3 + 1 + 1, tiene sumandos que no son mayores que siete.
En consecuencia, los diagramas de Ferrers ofrecen una sencilla demostración de la «bella ley de Euler», como la denominó Sylvester,
pk(n) = qk(n),
es decir, el número de particiones de n con k, o menos, sumandos es igual al número de particiones con sumandos que no exceden a k.

Veamos otro resultado sencillo que puede demostrarse con la ayuda de estos diagramas:
pk(n) = pk – 1(n) + pk(n – k).
Como ya hemos mencionado en más de una ocasión en la sección Matemoción del Cuaderno de Cultura Científica las demostraciones son una parte muy importante, de hecho, fundamental, de las matemáticas, por lo que este ejemplo nos sirve para ilustrar el proceso de una demostración matemática.
Vamos a demostrar la anterior fórmula. Es decir, la vamos a demostrar que pk(n) –el número de particiones del número n con k, o menos, sumandos- es igual a la suma de pk – 1(n) –el número de particiones del número n con k – 1, o menos, sumandos- y pk(n – k) –el número de particiones del número n – k con k, o menos, sumandos-. Para demostrarlo vamos primero a dividir el conjunto S de particiones del número n con k, o menos, sumandos en dos subconjuntos, a saber, el subconjunto S1 de particiones del número n con exactamente k sumandos y el conjunto S2 de particiones del número n con menos de k sumandos. Luego si contamos la cantidad de elementos de los subconjuntos S1 y S2, obtendremos que su suma es igual al número de elementos del conjunto S, esto es, pk(n).
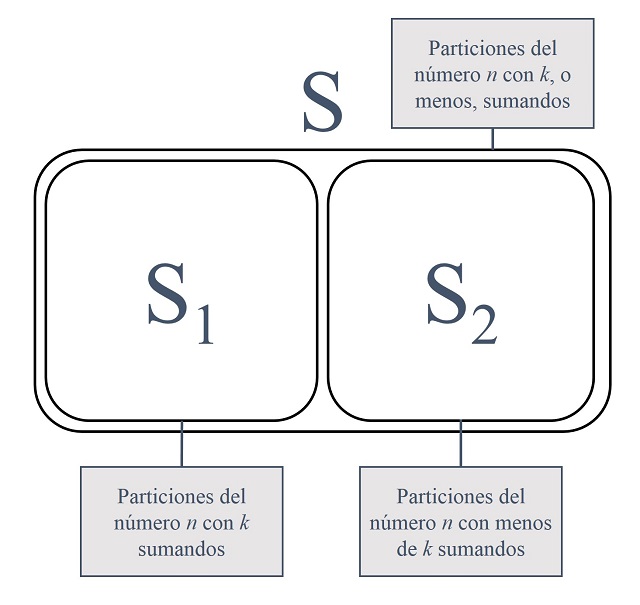
Pero claramente el conjunto S2 es igual al conjunto de particiones del número n – 1 con k, o menos, sumandos, de donde se deduce que la cantidad de elementos de S2 es igual a pk – 1(n).
Para obtener el número de elementos de S1 vamos a utilizar los diagramas de Ferrers. Como los elementos de S1 tienen exactamente k sumandos, sus diagramas de Ferrers tienen exactamente k filas, como se muestra en el ejemplo de la imagen, luego si se elimina la primera columna –que para cualquier elemento de S1 tiene k puntos- se obtiene una partición de n – k (ya que se han quitado k puntos) con k, o menos, sumandos. Por lo tanto, el número de elementos de S1 es pk(n – k).
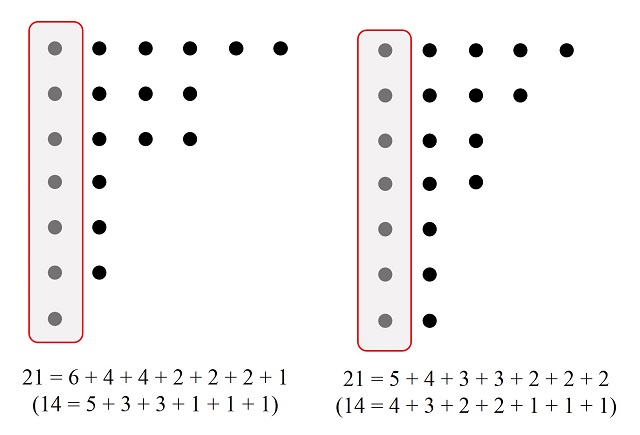
En conclusión, pk(n) es igual a la suma de las cantidades de elementos de S1 y S2, luego pk(n) = pk – 1(n) + pk(n – k); QED (Quod erat demonstrandum).
Otra propiedad, esta vez de las particiones autoconjugadas –aquellas particiones de un número que son iguales a sus conjugadas-, que se puede probar fácilmente de forma visual teniendo en cuenta los diagramas de Ferrers es la siguiente:
El número de particiones autoconjugadas es igual al número de particiones con números impares distintos.
La idea que subyace a esta prueba es que una línea con un número impar de puntos se puede plegar en una partición autoconjugada (con una única fila y una única columna, con la misma cantidad de puntos en ambas), como en la siguiente imagen.
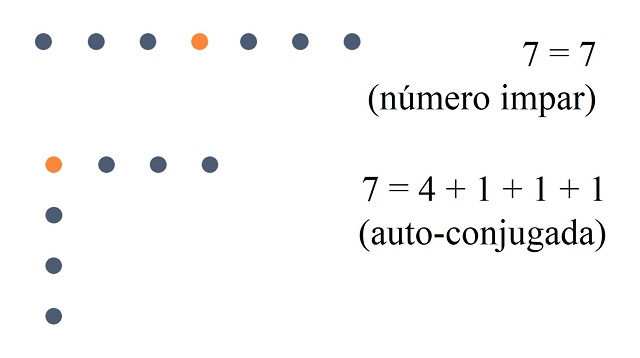
A partir de la anterior idea se puede observar que el número de particiones autoconjugadas es igual al número de particiones con números impares distintos, sin más que aplicar el plegado a cada una de las filas con un número impar de puntos, todos ellos distintos, como se muestra en la siguiente imagen.
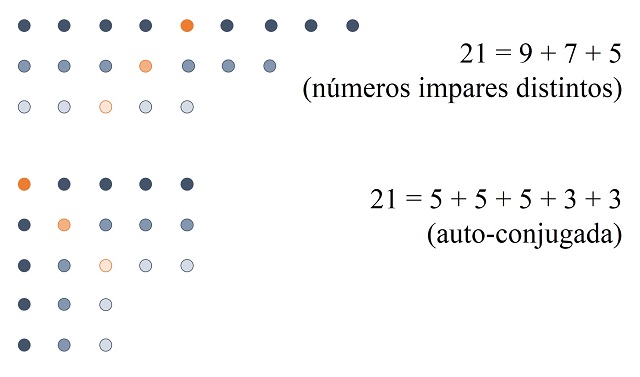
Observemos que si hay dos columnas con el mismo número impar de puntos no se genera una partición autoconjugada, como se muestra en el siguiente ejemplo.
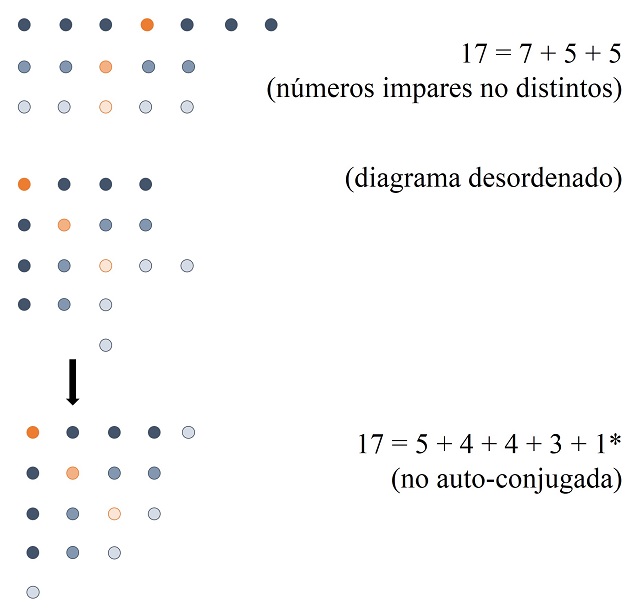
Estos ejemplos nos sirven para mostrar, una vez más, como en ocasiones podemos diseñar herramientas visuales potentes para realizar demostraciones matemáticas, como son el caso de los diagramas de Ferrers en el estudio de las particiones de los números.

Aunque pueda sorprender por su sencillez, las particiones de los números, como muchas otras herramientas de la combinatoria, tienen muchas aplicaciones en ciencia y tecnología. Aparecen en ocasiones en las que hay que contar determinado tipo de elementos o estructuras que pueden pensarse como particiones de los números. Por ejemplo, el matemático inglés Arthur Cayley se interesó en el estudio de la teoría de particiones como herramienta en el cálculo de ciertos invariantes algebraicos, pero lo mismo ocurre con muchas otras ramas de las matemáticas, y también de la física de partículas, la computación o la estadística, entre otras.
Más aún, las particiones están relacionadas, por ejemplo, con lo que en teoría combinatoria se llaman “problemas de ocupación”, que consisten en contar el número de formas de colocar una cierta cantidad de bolas n en una cierta cantidad de cajas k. Las particiones, en general, se corresponden con los problemas en los que las bolas son indistinguibles. Si las cajas son también indistinguibles, son las particiones propiamente dichas, y si son distinguibles, son las particiones ordenadas. Un ejemplo, de una aplicación de un problema de ocupación lo mostramos en la entrada Aprendiendo técnicas para contar: lotería primitiva y bombones.
Bibliografía
1.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.
2.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Contando lentejas, las particiones de los n&uac…
[…] Hace unos años escribí una biografía sobre el matemático británico Arthur Cayley (1821-1895), que es uno de esos matemáticos por los que siento cierta admiración. Arthur Cayley investigó prácticamente en todas las áreas de las matemáticas –escribió 967 artículos y un libro sobre funciones elípticas–, en un tiempo en el que la investigación matemática … […]