Algunos descubrimientos en matemáticas –y en ciencia en general– nacen de errores. Es algo que repetimos a menudo en el aula a nuestro alumnado: no deben temer equivocarse. En muchas ocasiones, el análisis de un error ayuda a entender un enunciado o un razonamiento con precisión.

En 1981, el matemático Lee Markowitz –de la Universidad de Bowling Green State, Ohio, EE. UU.– publicó un artículo en la revista Mathematics Teacher en la que precisamente comentaba cómo un error le había llevado a preguntarse sobre cierta propiedad relativa a triángulos.

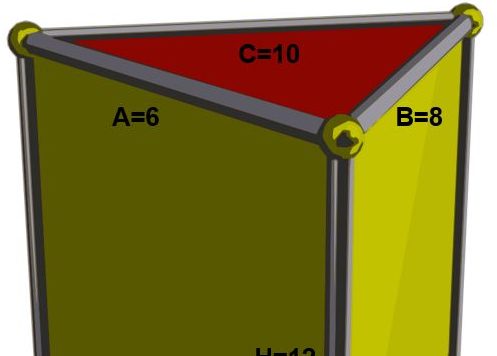
Mientras el matemático estaba explicando un ejercicio de geometría a uno de sus estudiantes, cometió un error que le llevó a preguntarse cuándo el perímetro y el área de un triángulo eran iguales. El ejercicio en cuestión consistía en calcular el área lateral de un prisma recto de base triangular. El triángulo tenía catetos de longitudes A=6 y B=8 unidades e hipotenusa de C=10 de largo, siendo la altura del prisma de H=12.

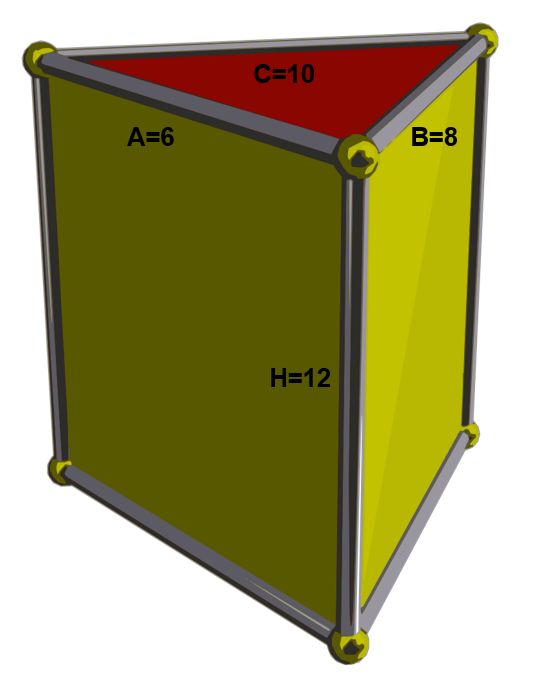
Recordemos que el área lateral de un prisma recto es PH, donde P es el perímetro de la base y H la altura del prisma.

Markowitz se equivocó y calculó el área del triángulo en vez de su perímetro. El error pasó desapercibido en un primer momento porque, efectivamente, el área del triángulo es AB/2 –es decir, 24– y el perímetro es A+B+C=6+8+10=24.

Al ser consciente del error, como buen matemático, Markowitz comenzó a hacerse varias preguntas.

• Cuestión 1: ¿Es este el único triángulo de lados de longitud natural cuyo perímetro y área coinciden?

• Cuestión 2: ¿Hay más triángulos cuyos lados tengan longitud racional, no necesariamente entera?

• Cuestión 3: ¿Existen triángulos no rectángulos, con lados de longitud natural y cuyo perímetro y área coincidan?

Y Markowitz comenzó a investigar, llegando a demostrar dos teoremas:

Teorema 1: Existen solo cinco triángulos con lados de longitud entera para los cuales el área coincide con el perímetro. Solo dos de estos triángulos son rectángulos.

Teorema 2: Existen infinitos triángulos rectángulos con lados de longitud racional para los cuales el área coincide con el perímetro.

Vamos a responder a las preguntas –a probar los teoremas– siguiendo las indicaciones de Lee Markowitz en su artículo.

Un triángulo de lados A, B y C (hipotenusa) respondiendo a la cuestión 1 debe verificar las siguientes propiedades:

1. A, B y C son números naturales,
2. el área del triángulo coincide con su perímetro, es decir, ½AB=A+B+C, y
3. el triángulo es rectángulo, es decir, A²+B²=C².

Despejando C de (2) se deduce que C=½AB-A-B. Y sustituyendo C en la condición (3) queda que A²+B²=(½AB-A-B)², es decir, AB(AB-4A-4B+8)=0. Como A y B son positivos, debe ser AB-4A-4B+8=0. De otro modo, se obtiene la condición:

4. (A-4)(B-4)=8.

Considerando dos triángulos rectángulos iguales si se intercambian los papeles de los dos catetos, solo hay dos soluciones que verifican (1), (2), (3) y (4), a saber (A,B,C)=(6,8,10) y (A,B,C)=(5,12,13). El resultado se obtiene fácilmente al tener en cuenta que 8 se puede escribir como producto de números naturales solo de dos maneras: como el producto de 1 por 8 o el de 2 por 4.

La cuestión 2 se resuelve eliminando la condición (1), es decir, estudiando aquellos triángulos verificando únicamente (2) y (3). Así, debe resolverse la condición (4) permitiendo valores racionales positivos para A y B. Despejando B de (4), se obtiene la ecuación

5. B=(-8+4A)/(A-4).

El cociente de -8+4A entre A-4 es positivo cuando A es mayor que 4 o cuando A es menor que 2 (y positivo). Esto prueba que hay infinitos triángulos con lados racionales cuya área y perímetro coinciden.

Y, para finalizar, asumamos que el triángulo no tiene que ser rectángulo, aunque debe tener lados enteros. Así, debemos eliminar la condición (3) del análisis. El área de un triángulo no rectángulo en términos de la longitud de sus lados no se escribe como en (2). La expresión del área sigue la llamada fórmula de Herón –que, por supuesto, corresponde a la condición (2) en el caso de un triángulo rectángulo– es la raíz cuadrada de S(S-A)(S-B)(S-C), donde S es el semiperímetro del triángulo. Así la cuestión 3 se resuelve imponiendo las condiciones (1) y

6. S(S-A)(S-B)(S-C)=(A+B+C)².

Analizando (1) y (6) –simplificando la ecuación (6) y descartando las soluciones no enteras– se obtienen cinco pares de triángulos que cumplen esas condiciones, a saber: (A,B,C)=(6,8,10), (A,B,C)=(5,12,13), (A,B,C)=(6,25,29), (A,B,C)=(7,15,20) y (A,B,C)=(9,10,17). Las dos primeras corresponden a los triángulos rectángulos ya citados con anterioridad.

Así hemos demostrado los dos teoremas enunciados por Lee Markowitz; son hermosos y sencillos resultados fruto de un error… y de la tan necesaria curiosidad en la actividad investigadora.

Referencias

[1] Math Notes, Futility Closet, 23 enero 2020.

[2] Lee Markowitz, Area = Perimeter, Mathematics Teacher 74:3 (1981), 222-223.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.