Con la anterior entrada del Cuaderno de Cultura Científica titulada Teoremas geométricos sin palabras: Viviani iniciamos una pequeña serie estival de demostraciones sin palabras de interesantes y hermosos teoremas geométricos. El teorema de la anterior entrada era un teorema clásico de la geometría del plano sobre triángulos equiláteros, el conocido teorema de Viviani. Este resultado del matemático italiano Vincenzo Viviani (1622-1703) dice que “la suma de las distancias de un punto cualquiera en el interior de un triángulo equilátero (o en alguno de sus lados) a cada uno de sus lados es igual a la altura del mismo.”

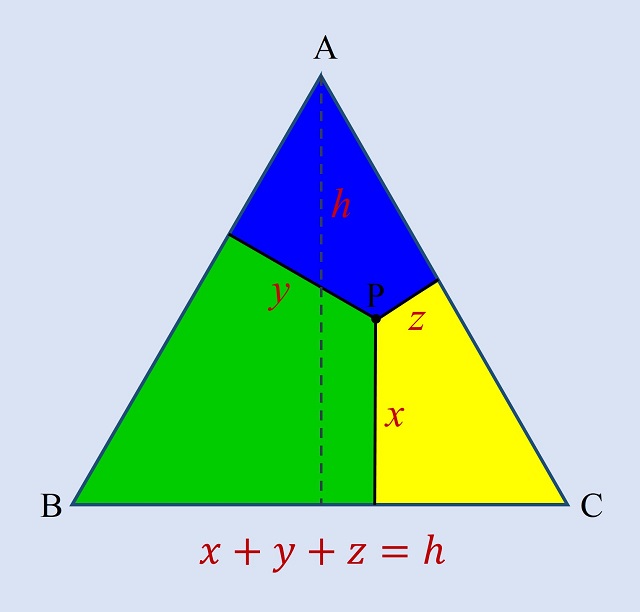
En esta entrada, vamos a pasar de un extremo al otro, de un teorema clásico, el teorema de Viviani, de hace más de 300 años, a un teorema actual, el teorema de la circunferencia de Conway. El matemático británico John Horton Conway (1937-2020), fallecido recientemente como consecuencia del covid-19, fue un prolífico e imaginativo matemático que trabajó en muchas áreas de las matemáticas, entre ellas la teoría de grupos algebraicos, las matemáticas de los juegos, la teoría de nudos, la teoría de números, la geometría o la teoría de códigos, que escribió interesantes libros, como la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), junto a Richard K. Guy y Elwyn Berlekamp, o The Book of Numbers (El libro de los números), con Richard K. Guy, y que es conocido por temas como el autómata celular denominado el juego de la vida, los números surreales o la regla del fin del mundo, entre muchos otros.

Pero antes de adentrarnos en el teorema de la circunferencia de Conway, vayamos a la resolución del problema que dejamos planteado en la anterior entrada y que podía resolverse con una sencilla prueba sin palabras.

El cuadrado dentro del cuadrado

El problema, que habíamos planteado en la anterior entrada y que dejamos pendiente para todas aquellas personas que quisierais intentar resolverlo de una forma sencilla, es el siguiente.

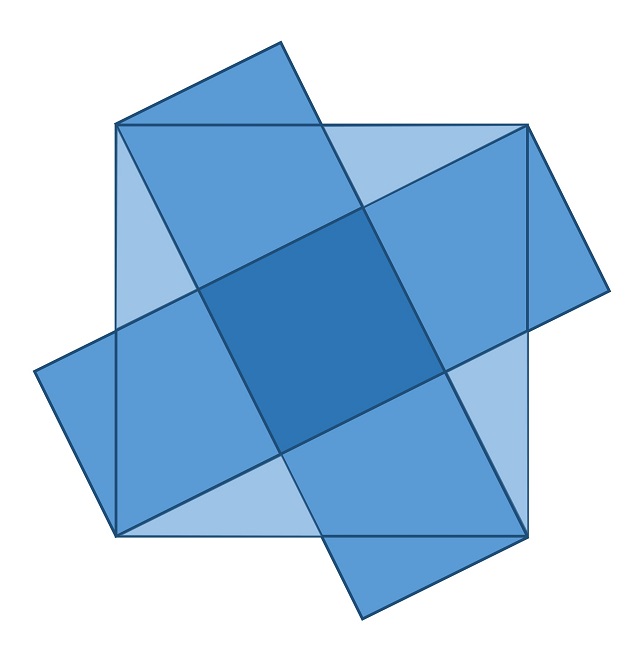
Problema (El cuadrado dentro del cuadrado): Demuéstrese que si se trazan rectas que unen los vértices del cuadrado con los puntos medios de uno de los lados opuestos, como se muestra en la siguiente imagen, entonces el área del cuadrado central es un quinto del área del cuadrado original.

Como hemos comentado, este problema se puede resolver fácilmente de forma visual. Si nos fijamos en el siguiente dibujo, deduciremos que, como se afirma en el problema, el área del cuadrado central es igual la quinta parte del área del cuadrado grande.

El teorema de la circunferencia de Conway

El 15 de abril de 2020, con motivo de la muerte del matemático británico John H. Conway unos días antes, el 11 de abril, el matemático Matt Baker escribió en su blog Matt Baker’s Math Blog una entrada titulada Some Mathematical Gems from John Conway (Algunas joyas matemáticas de John Conway), en la que hacía un repaso personal de algunas de las contribuciones de este genial matemático. Una de esas contribuciones, que yo no conocía y que llamó mi atención, es uno de esos curiosos resultados geométricos que entraría de lleno en los objetivos de esta serie estival, puesto que es sorprendente, interesante e incluso se ha realizado una hermosa demostración sin palabras del mismo.

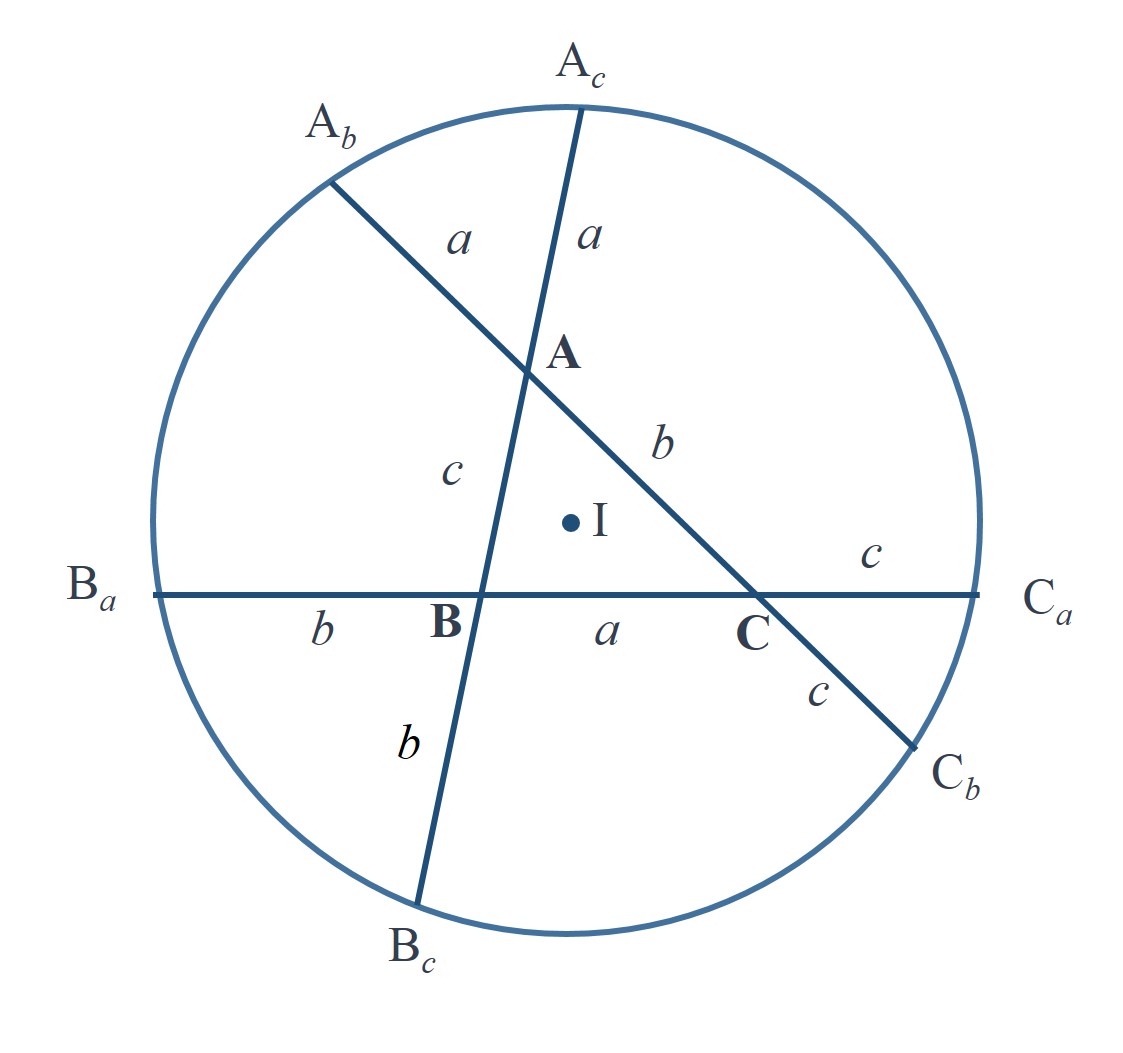
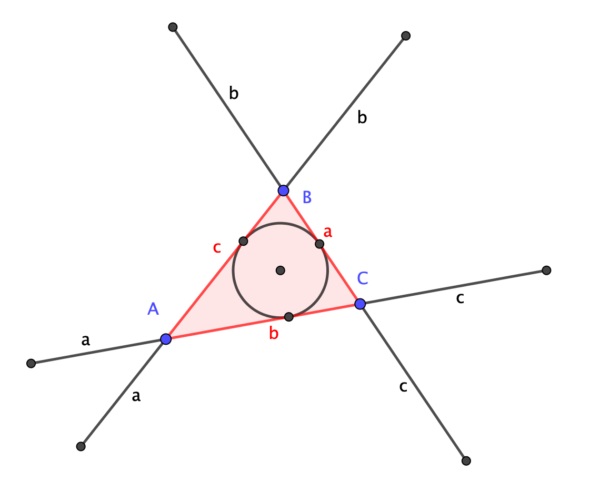
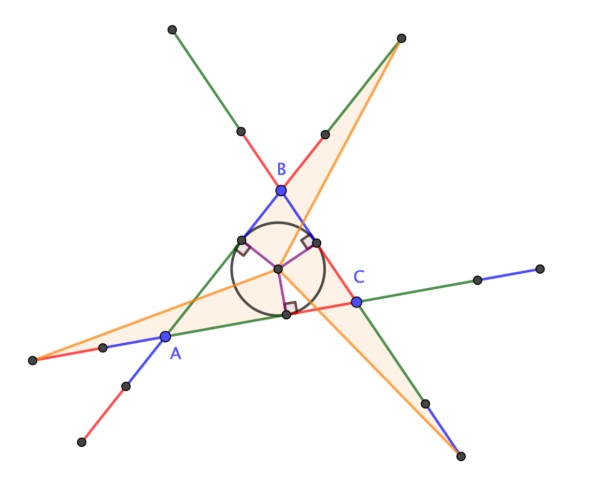
El inventor del juego de la vida descubrió la siguiente propiedad geométrica de los triángulos, en concreto, observó que, si los lados de un triángulo que se encuentran en un vértice son extendidos por una longitud igual al lado opuesto, los seis puntos finales de los seis segmentos rectos resultantes se encuentran en una misma circunferencia cuyo centro es, además, el incentro del triángulo, es decir, el centro de la circunferencia inscrita en el triángulo.

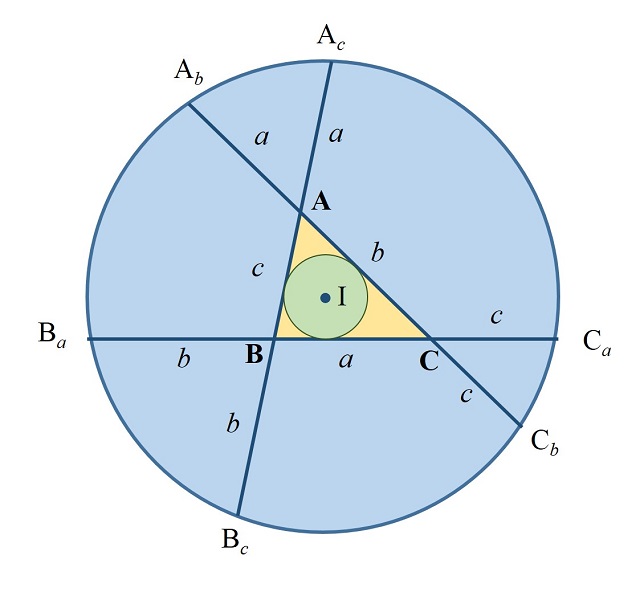
Teorema de la circunferencia de Conway: Dado un triángulo ABC, de lados a = BC, b = AC y c = AB (como se muestran en la imagen), se extienden los lados a, b y c, y se consideran los puntos A_b y A_c, que están a una distancia a en las rectas extensión de b y c, es decir, AA_b = AA_c = a, de igual forma se consideran los puntos B_a y B_c, que están a una distancia b en las rectas extensión de a y c, y C_a y C_b, que están a una distancia c en las rectas extensión de a y b, entonces los puntos A_b, A_c, B_a, B_c, C_a y C_b son concíclicos, es decir, están en una misma circunferencia, a la cual se denomina “circunferencia de Conway”. Más aún, el centro de la circunferencia de Conway es el incentro del triángulo ABC.

Al parecer John Conway nunca publicó nada de este resultado geométrico. Según aparece recogido en el blog de la matemática Tanya Khovanova (Tanya Khovanova’s Math Blog), el matemático tenía una camiseta del campamento de verano de matemáticas Mathcamp de 1998 en el que aparecía una ilustración de este teorema con la expresión “la circuferencia de Conway”, que vemos en la siguiente imagen. Es probable que Conway solo lo presentara de forma oral en estos campamentos o en algún evento similar.

Sobre esta fotografía su autora comenta que “el pobre John Conway tuvo que estar de espaldas a mí hasta que descubrí la prueba del teorema y me di cuenta de qué punto debía ser el centro de la circunferencia de Conway”.

A partir del fallecimiento de Conway y la publicación del matemático Matt Baker en su blog, empezaron a publicarse diferentes demostraciones del teorema de la circunferencia de Conway, como se recoge en la página web del matemático irlandés Colm Mulcahy. Por ejemplo, la matemática estadounidense Doris Schattschneider obtuvo dos demostraciones en 2020 (abril y mayo), de la segunda de las cuales dijo que “es mucho más bonita y convincente. Una demostración que creo que Conway habría sido más propenso a realizar él mismo”, basada en un hexágono y que puede leerse en la página de Colm Mulcahy.

Sin embargo, la demostración que recogemos aquí fue obtenida por el matemático británico Alex Ryba, en mayo de 2020. Es una demostración sencilla basada en triángulos isósceles. Mostramos una ilustración con el triángulo ABC y las extensiones de longitudes a, b y c en los vértices A, B y C, con los puntos extremos A_b, A_c, B_a, B_c, C_a y C_b, que son los que hay que demostrar que están en una circunferencia de centro I, el incentro del triángulo ABC, es decir, que todos ellos equidistan del punto I.

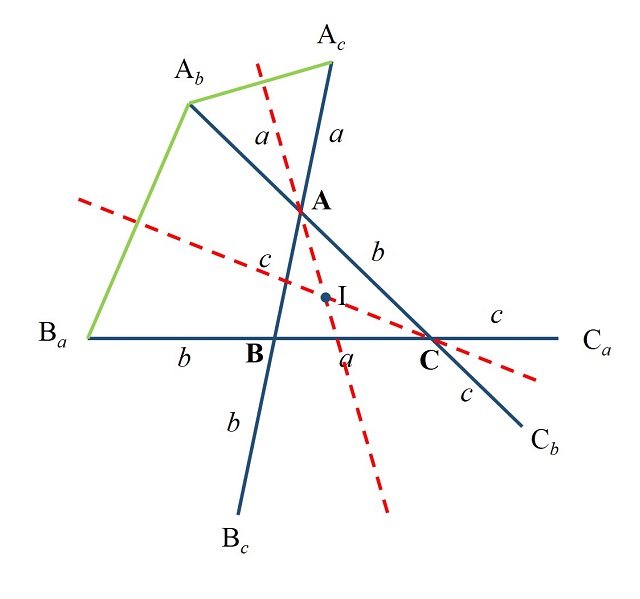
La demostración de Ryba es la siguiente: Los triángulos A_bAA_c y B_aCA_b son triángulos isósceles, con ápices (es decir, los vértices formados por los lados iguales) A y C, por lo tanto, las rectas mediatrices de las bases A_bA_c y B_aA_b (en rojo en la imagen) son además las rectas que bisecan los ángulos en los ápices A y C (llamadas bisectrices), luego son las bisectrices de los ángulos en A y C del triángulo ABC, luego se intersecan en el incentro I del triángulo ABC (esto es debido a que el incentro del triángulo es también el punto en el que se intersecan las tres bisectrices del mismo). Además, puesto que las rectas son las mediatrices de las bases A_bA_c y B_aA_b, y se cortan en I, entonces los puntos B_a, A_b y A_c equidistan de I. Argumentos similares nos determinan que los puntos C_b, B_c y B_a equidistan de I, así como A_c, C_a y C_b. Y el resultado queda probado.

Y han ido apareciendo más demostraciones del resultado, pero también se han descubierto demostraciones anteriores, como la publicada por el matemático cordobés Francisco Javier García Capitán en Forum Geometricorum, en 2013, en el artículo A Generalization of the Conway Circle. En este artículo se menciona que “esta configuración también apareció en el Problema 6 de la Olimpiada Matemática Iberoamericana de 1992”.

Respecto a la demostración sin palabras de este resultado geométrico, en 2020 el matemático británico Colin Beveridge, autor de libros como La biblia de las matemáticas, Guía para comprender y disfrutar el mundo de las matemáticas (Gaia, 2016) o Lo que las Matemáticas Esconden… Descubre las Matemáticas del Día a Día (Libsa, 2019), publicó en el blog The Aperiodical una hermosa demostración sin palabras del teorema de la circunferencia de Conway. Esta demostración consiste en una serie de seis imágenes que incluimos a continuación, que os dejamos para que seáis vosotros mismos quienes comprobéis que efectivamente demuestra el teorema de la circunferencia de Conway.

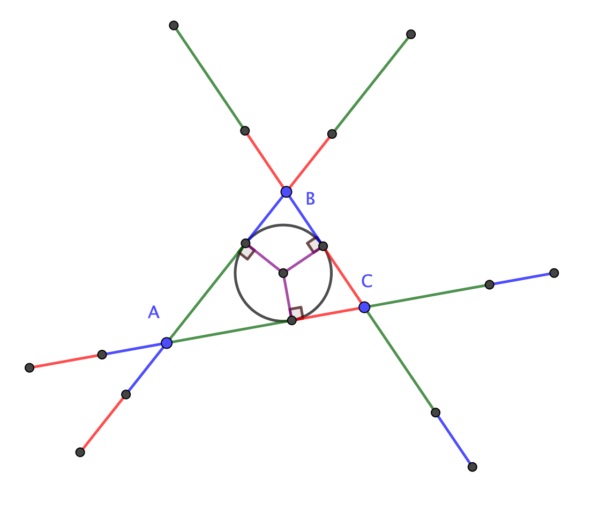
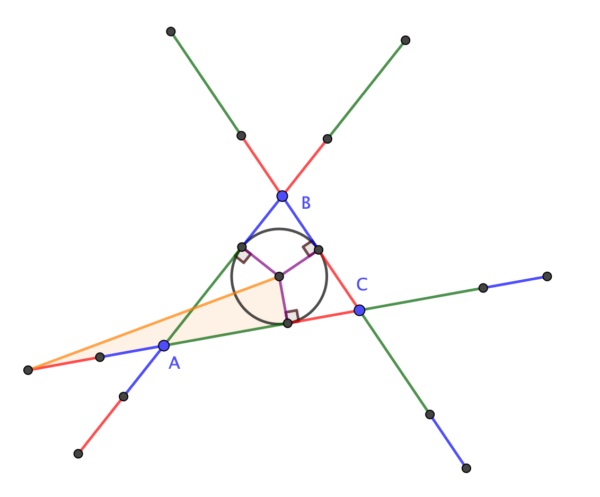
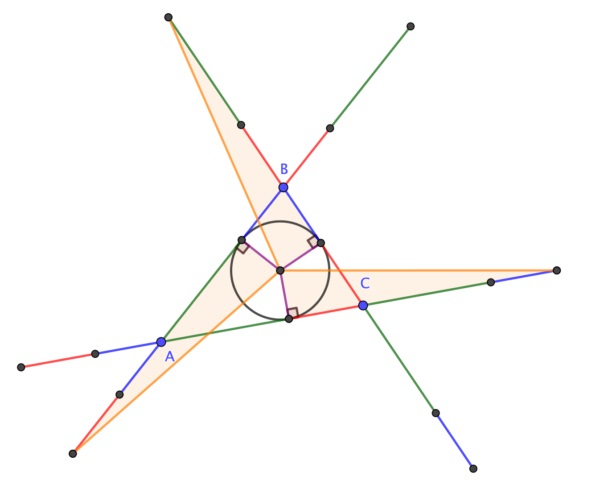
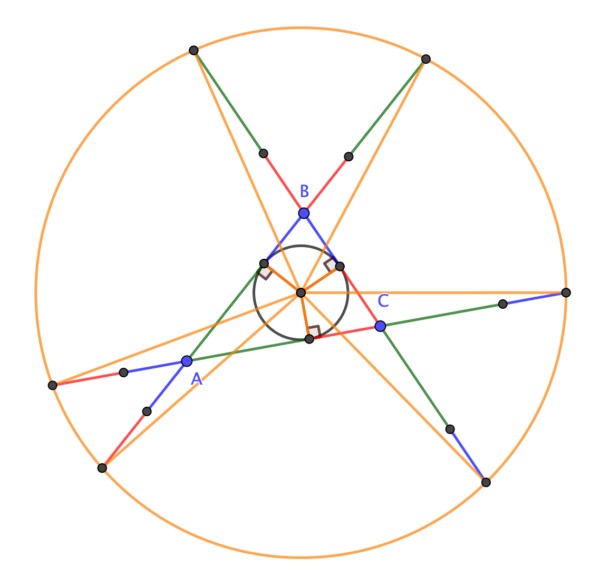
Un cuadrado inscrito en un triángulo

Al igual que en la anterior entrada, vamos a terminar esta con otro sencillo problema que puede ser resuelto con un razonamiento visual. Este problema, como el de la primera entrada de esta serie estival, es otro problema sobre cuadrados que aparece recogido en el artículo A Round-Up of Square Problemas (Una recopilación de problemas con cuadrados), de los matemáticos Duane Detemple y Sonia Harold, publicado en Mathematics Magazine en 1996.

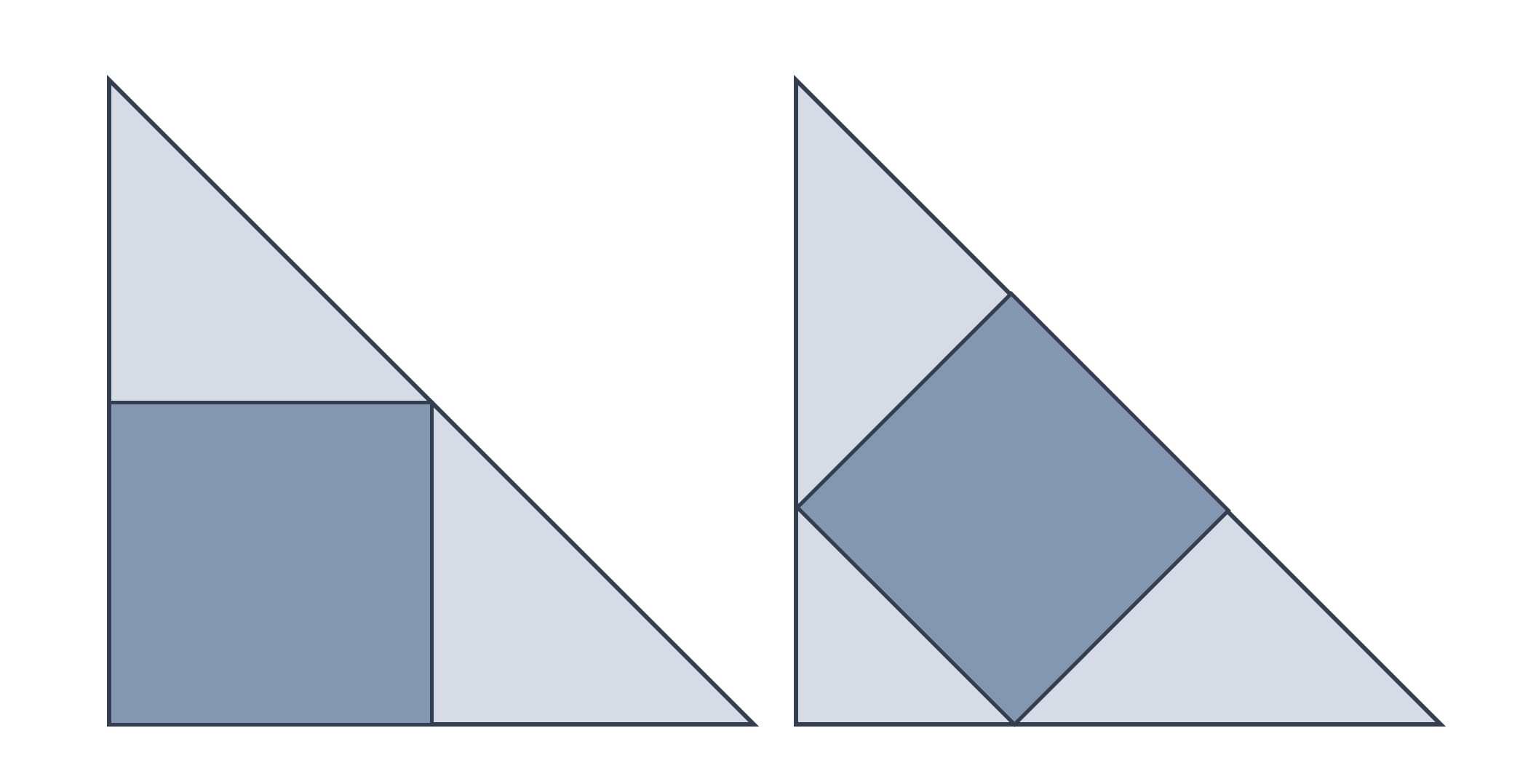
Problema (Un cuadrado inscrito en un triángulo rectángulo isósceles): Estos dos cuadrados han sido inscritos en un mismo triángulo rectángulo isósceles, pero de dos formas distintas, como se muestra en la imagen. ¿Cuál de los dos cuadrados tiene una mayor superficie?

Bibliografía:

1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.

2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.

3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.

4.- Wolfram MathWorld: Conway circle (Darij Grinberg y Eric W. Weisstein)

5.- Francisco Javier García Capitán, A Generalization of the Conway Circle, Forum Geometricorum, vol. 13, pp. 191-195, 2013.

6.- Duane Detemple y Sonia Harold, A Round-Up of Square Problemas, Mathematics Magazine 69, no. 1, pp. 15-27, 1996.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica