Entre los individuos, la amistad nunca viene dada, sino que debe conquistarse indefinidamente.

Simone de Beauvoir

Decir amistad es decir entendimiento cabal, confianza rápida y larga memoria; es decir, fidelidad.

Gabriela Mistral

Recordemos que, en matemáticas, un grafo está definido por un conjunto de vértices y un conjunto de aristas uniendo algunos de estos vértices. Un grafo se llama plano cuando puede dibujarse en el plano sin que ninguna arista se cruce. Los ejemplos más sencillos de grafos no planos son los conocidos como K₅ y K_3,3.

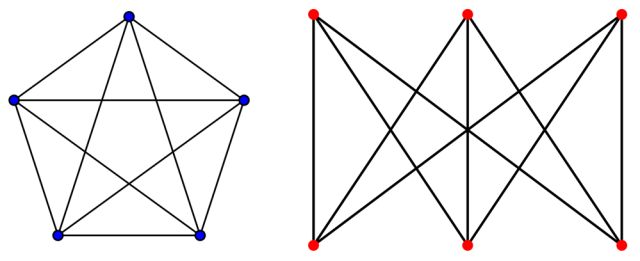
De hecho, en 1930, el matemático y lógico Kazimierz Kuratowski (1896-1980) demostró este bello teorema que caracteriza la ‘planitud’ de cualquier grafo:

Un grafo es plano si y solo si no contiene ningún subgrafo homeomorfo a K₅ o K_3,3.

El grafo de la amistad F_nse construye uniendo n copias del grafo cíclo C₃ a través de un vértice común.

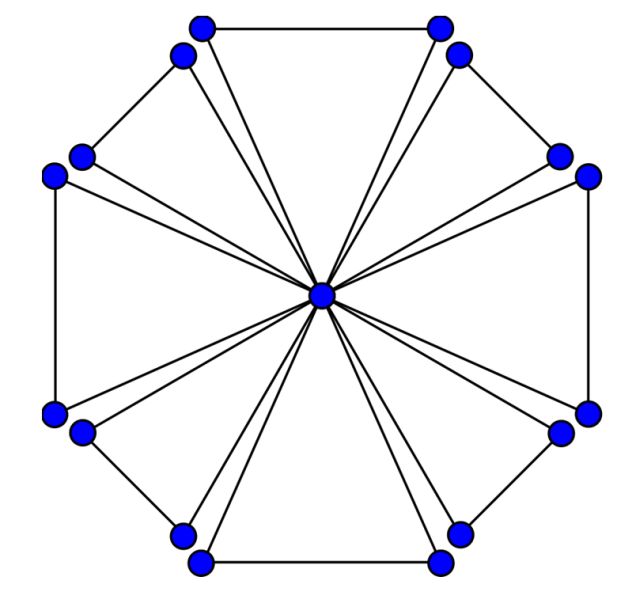
Se trata de un grafo plano que posee 2n+1 vértices y 3n aristas.

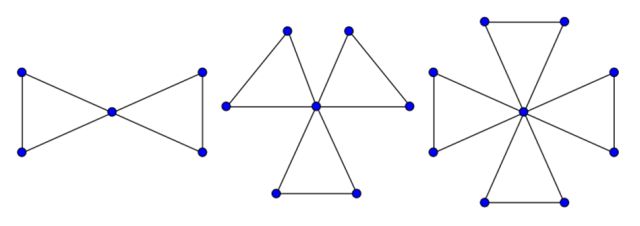
En 1966 Paul Erdős, Alfréd Rényi y Vera T. Sós demostraron el que llamaremos el primer teorema de la amistad, que dice lo siguiente (ver [2]):

Los grafos finitos con la propiedad de que dos vértices cualesquiera tienen exactamente un vértice vecino en común son precisamente los grafos de la amistad.

Una manera de pensar en este teorema –y de allí su nombre– es el siguiente: si un grupo de personas posee la característica de que cada par de ellas tiene exactamente un amigo en común, entonces debe de haber una persona que sea amiga de todas las demás.

El primer teorema de la amistad no funciona para grafos infinitos, es decir, pueden existir grafos infinitos diferentes, con la propiedad de que ‘dos vértices cualesquiera tienen exactamente un vértice vecino en común’ y con el mismo cardinal (ver [3]).

Por cierto, Vera T. Sós (1930) es una especialista en combinatoria. Esa “T.” corresponde al apellido de su marido, Pál Turán (1910-1976). Ambos fueron estudiantes de Lipót Fejér… y ambos poseen número de Erdős igual a 1.

Para establecer el segundo teorema de la amistad, supongamos que en una fiesta hay 6 personas. Si tomamos dos de ellas al azar, o bien se encuentran por primera vez –les llamaremos mutuamente extraños– o bien se conocían previamente –los llamaremos mutuamente conocidos–. El teorema dice entonces lo siguiente:

En cualquier grupo de seis personas, existen tres personas que son mutuamente conocidas o mutuamente desconocidas.

Este problema puede reformularse en términos de teoría de grafos. Recordemos que un grafo se llama completo si es un grafo simple –sin aristas múltiples entre vértices, en particular, sin bucles– donde cada par de vértices está conectado por una arista. Un grafo completo de n vértices se denota K_n –antes hemos hablado de K₅–.

K₆ contiene 15 aristas.

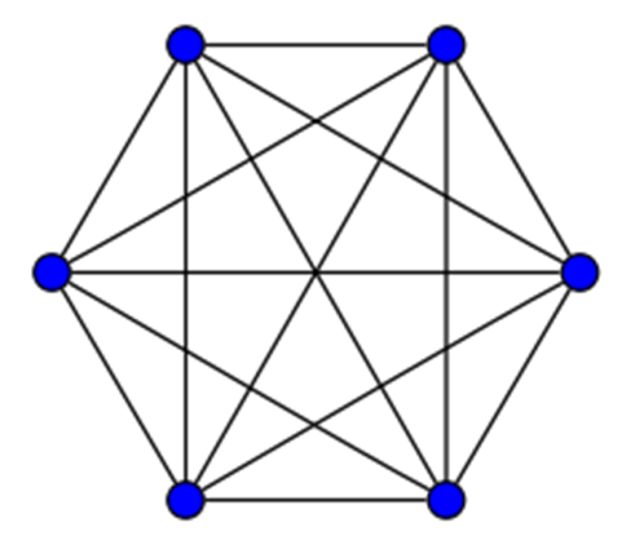
Cada persona asistente a esa fiesta se puede representar por uno de los vértices. Coloreemos la arista uniendo dos vértices de rojo si las personas correspondientes son mutuamente conocidas y de azul si son mutuamente extrañas.

El segundo teorema de la amistad se reformula entonces en términos de coloreado de grafos:

Si coloreamos con rojo o azul las 15 aristas de K₆ siempre habrá un triángulo rojo o un triángulo azul.

La prueba es muy sencilla. Elegimos un vértice cualquiera V. Cinco aristas inciden con V, y serán de color rojo o azul. El principio del palomar garantiza que al menos tres aristas deben ser del mismo color; supongamos que es rojo. Llamemos A, B y C los vértices correspondientes a estas tres aristas. Si alguna de las aristas AB, BC, CA es roja, entonces esta arista junto con las dos aristas incidentes a V forman los lados de un triángulo rojo. Si ninguna de las aristas AB, BC, CA es roja, entonces las tres aristas son de color azul y se tiene el triángulo azul ABC.

El matemático Frank P. Ramsey (1903-1930) demostró un teorema general de combinatoria en su artículo On a problem of formal logic, este fue el origen de la llamada teoría de Ramsey. El segundo teorema de la amistad es un caso particular de este resultado.

Por cierto, el segundo teorema de la amistad no funciona para grupos de menos de 6 personas…

Referencias

[1] Dutch Windmill Graph, Wolfram MathWorld

[2] Paul Erdős, Alfréd Rényi and Vera T. Sós, On a problema of graph theory, Studia Scientiarum Mathematicarum Hungarica 1 (1966) 215-235

[3] Václav Chvátal, Anton Kotzig, Ivo G Rosenberg and Roy O. Davies, Roy O., There are 2^ℵα friendship graphs of cardinal ℵ_α, Canadian Mathematical Bulletin 19 (4) (1976) 431-433

[4] Teorema de la amistad, Wikipedia (consultado el 18 septiembre 2019)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.