En 1975, el divulgador científico Martín Gardner (1914-2010) publicaba un artículo (ver [1]) en el que afirmaba que el denominado mapa de Mc.Gregor –de 110 regiones– precisaba necesariamente de cinco colores para pintarse, sin que dos regiones adyacentes compartieran color. Es decir, proponía un contraejemplo al teorema de los cuatro colores. ¿Por qué continuaron entonces Appel y Haken intentando demostrar el resultado planteado por Guthrie en 1852?

El artículo de Gardner se publicó el 1 de abril de 1975, el Día de los inocentes en los países anglosajones. Muchos lectores, contrariados, enviaron a Gardner propuestas de coloreado del mapa de Mc.Gregor, para mostrarle que su afirmación era errónea.

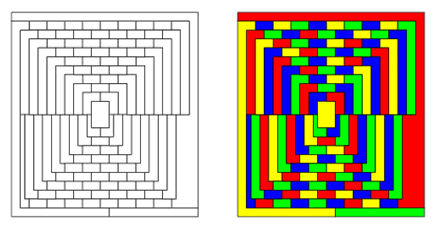
Lo raro es que esos lectores no fueran conscientes de que se trataba de una simple broma; en ese artículo Gardner hablaba de Seis descubrimientos sensacionales que de alguna manera han escapado a la atención pública. En efecto, el divulgador:

1. ‘mostraba’ una refutación de la teoría de la relatividad de Einstein, a través de un experimento del físico británico Humbert Pringl;

2. ‘anunciaba’ el descubrimiento –en el Codex Madrid I y por parte de Augusto Macaroni de la Universidad Católica de Milán– de que Leonardo de Vinci había inventado el retrete auto-limpiable con el agua de su cisterna;

3. ‘comentaba’ la demostración de Richard Pinkleaf –con ayuda del ordenador MacHic– de que en ajedrez, el movimiento de apertura de peón a cuatro torre de rey gana siempre la partida;

4. ‘notificaba’ el sorprendente resultado –obtenido por John Brillo de la Universidad de Arizona– de que la base de los logaritmos naturales, el número e,elevado a π(163)^½ es el número entero 262.537.412.640.768.744;

5. ‘anunciaba’ la construcción –debida al parapsicólogo Robert Ripoff– de un motor funcionando con energía mental; y

6. ‘notificaba’ el descubrimiento –por parte del especialista en teoría de grafos William McGregor– del famoso mapa del que hemos hablado antes.

Así que es lógico que, tras el 1 de abril de 1975, se continuara con la búsqueda de una demostración del teorema de los cuatro colores… Durante el largo proceso hasta llegar a su prueba, se desarrollaron teorías matemáticas como la teoría de grafos y de redes. Es decir, ni los errores ni los aciertos intentando demostrar este teorema fueron nimios; todos ellos ayudaron a la puesta a punto de este primer gran teorema demostrado –¿verificado?– usando un ordenador.

Pero, ¿es realmente una demostración? ¿Se puede garantizar la corrección de la compilación realizada por un ordenador? ¿Las computadoras son infalibles? Tras la demostración del teorema de los cuatro colores con ayuda de ordenadores, otras pruebas se apoyaron en este método, como la clasificación de los grupos simples finitos (2004) –que depende de cálculos imposibles de ejecutar con detalle a mano– o la solución de Thomas Hales (1998) del problema de Kepler sobre el empaquetamiento óptimo de esferas. Pero, ¿se puede aceptar como válida una afirmación que sólo una máquina, y no una mente humana, puede comprobar?

¿Qué es una demostración? El filósofo de la ciencia Imre Lakatos (1922-1974) la define (ver [3]) como: “Una sucesión finita de fórmulas de algún sistema dado, donde cada uno de los pasos de la sucesión es o bien un axioma del sistema, una fórmula derivada por una regla del sistema a partir de una fórmula precedente”.

Por su parte, el filósofo Thomas Tymoczko (1943-1996) califica una demostración como algo (ver [6]): convincente –debería persuadir incluso a los escépticos que dudan de la veracidad del resultado–, formalizable –la conclusión debería alcanzarse partiendo de sistemas axiomáticos–, y comprobable.

Este último es el aspecto más controvertido en el caso del teorema de los cuatro colores. ¿Puede estar un teorema probado si no se puede leer (comprobar) su demostración?

Existen dos corrientes principales que intentan responder a este dilema:

Los escépticos opinan que el aspecto de la comprobabilidad es el que pone en duda la credibilidad de la prueba. Si las pruebas deben ser verificadas, parece que entonces una persona –lo opuesto a una máquina– debe completar esta tarea: esto no puede hacerse con la prueba del teorema de los cuatro colores.

El matemático Paul Halmos (1916-2006) opinaba que la demostración realizada con un ordenador tiene la misma credibilidad que si está hecha por un adivino…Y afirmaba: “No puedo aprender nada de la demostración. La prueba no indica la razón por la que sólo se necesitan 4 colores ¿por qué no 13? ¿Qué tiene de especial el número 4?”.

El matemático Pierre Deligne (1954) comentaba: “No creo en una prueba hecha con ordenador. En primer lugar, soy demasiado egocéntrico. Creo en una demostración si la entiendo, si está clara. Un ordenador puede también cometer errores, pero es mucho más difícil encontrarlos”.

Tymockzo afirma que usar un ordenador para establecer una verdad matemática es transformar pruebas en experimentos. Afirma que el teorema de los cuatro colores ha sido confirmado a través de un experimento de física teórica, pero no probado de una manera formal. Aunque se tiene una pequeña idea de lo que el ordenador está testando, no se tiene la seguridad de lo que se está haciendo.

Los no escépticos, por su parte, argumentan del siguiente modo:

1. aunque las equivocaciones cometidas por los ordenadores son más difíciles localizar, los seres humanos fallan con más frecuencia; los ordenadores siguen un programa rígido predeterminado, y no tienen tropiezos motivados por los cambios de humor, el estrés u otros factores externos;

2. la longitud de algunas demostraciones sobrepasa la capacidad de computación humana, pero es perfectamente aceptable por los estándares de las máquinas;

3. la idea de que no pueden usarse ordenadores va a ser cada vez más insólita para las generaciones futuras: los ordenadores serán –¿son?– herramientas como el lápiz y el papel…

4. la prueba de Appel y Haken es, en esencia, tradicional, ya que consiste en una serie de pasos lógicos, que conducen a la conclusión de que la conjetura puede reducirse a una predicción sobre el comportamiento de unos2.000 mapas.

¿Quiénes tienen razón?

Para añadir un poco más de incertidumbre al tema, el filósofo Hud Hudson afirmaba dar en [2] un contraejemplo al teorema de los cuatro colores: presentaba el mapa de Zenopia, una isla formada por seis provincias que necesita seis tonos para colorearse… Entonces, ¿es falso el teorema de los cuatro colores? No, no hay que preocuparse: Zenopia es un mapa con fronteras extrañas, cuya especial geografía queda excluda del enunciado original del teorema…

Bibliografía

[1] Martin Gardner, Mathematical Games: Six Sensational Discoveries that Somehow or Another have Escaped Public Attention, Scientific American 232, 127-131, 1975

[2] Hud Hudson, No basta con cuatro colores, Gaceta de la RSME 8(2), 361-368, 2005.

[3] Imre Lakatos, What does a mathematical proof prove?, Cambridge Univers¡ity Press, 540-551, 1979.

[4] Marta Macho Stadler, Mapas, colores y números, Descubrir las matemáticas hoy: Sociedad, Ciencia, Tecnología y Matemáticas 2006 (2008) 41-68

[5] E.R. Swart, The philosophical implications of the four-colour theorem, American Mathematical Montlhy 87, 697-707, 1980

[6] Thomas Tymoczko, The four-color problem and its philosophical significance, Journal of Philosophy 76, 57-70, 1979

[7]Robin .J. Wilson, Four colors suffice: how the map problem was solved, Princeton University Press, 2002

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.