En la anotación La magia del teorema de Zeckendorf hablábamos de un truco de magia realizado con diez cartas y que se basaba en una propiedad matemática relacionada con la teoría aditiva de númerosi. Esa propiedad se conoce como el teorema de Zeckendorf, y afirma que:
Todo entero positivo se escribe, de manera única, como suma de números de Fibonacci no consecutivos. A esa escritura única se le llama la descomposición de Zeckendorf del número en cuestión.

Este teorema lleva el nombre del matemático amateur Édouard Zeckendorf (1901-1983) e involucra a los números definidos por la sucesión de Fibonacci, serie que comienza con el 0 y el 1, y cada término se obtiene al sumar los dos anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Para que quede más claro, vamos a calcular la descomposición de Zeckendorf del número 100. Para ello tomamos el mayor número de Fibonacci que es menor o igual que 100, que es el 89. Se hace la diferencia 100 – 89 = 11 y se procede del mismo modo. El mayor número de Fibonacci que es menor o igual que 11 es 8; se hace la diferencia 11 – 8 = 3, que ya es un número de Fibonacci, con lo que la descomposición de Zeckendorf de 100 es: 100 = 89 + 8 + 3.
Es cierto que hay otras descomposiciones de 100 como sumas de números de Fibonacciii, pero solo la anterior consta de números de Fibonacci no consecutivos. La demostración de este teorema, tanto la existencia como la unicidad de la descomposición, puede hacerse por recurrencia.
Poesía “a la Zeckendorf”
En 1979, el matemático y miembro del grupo OuLiPo (Ouvroir de Littérature Potentielle) Paul Braffort (1923-2018) rindió homenaje al teorema de Zeckendorf a través del poemario Mes hypertropes. Vingt-et-un moins un poèmes à programme (Mis hipertropos. Veintiún menos un poemas con programa).

Se trata de una serie de veinte poemas cuya estructura interna se rige por este teorema matemático: el poema n tiene en cuenta los poemas correspondientes a la descomposición de Zeckendorf de ese número n. Por ejemplo, como el número 12 se escribe como 8 + 3 + 1 según el teorema de Zeckendorf, esto indica que el poema número 12 comparte algunos contenidos de los poemas 1, 3 y 8 de Mes hypertropes. Esta restricción oulipiana obliga a Braffort a construir marcos que permitan estas conexiones entre algunos de los poemas de la serie.
Los números 1, 2, 3, 5, 8 y 13 son su propia descomposición de Zeckendorf, así que Braffort relaciona estos poemas con los dos números de Fibonacci que lo generan. Por ejemplo, como 8 = 3 + 5, el poema 8 comparte contenido con el 3 y el 5. Eso significa que solo el primer poema L’explication préalable ou la raison des rimes (La explicación previa o el motivo de las rimas) no se ve influenciado por ninguno de la serie.
Tras el índice, el autor explica brevemente cómo se estructura el textoiii:
Los poemas que van a leer se han diseñado respetando el “principio de Roubaudiv” que se enuncia de este modo:
Solo se utilizará una estructura matemática como restricción clave de una obra literaria si se incluyen uno o varios teoremas relacionados con esta estructura.
Nuestra “estructura” es aquí la de la sucesión de Fibonacci, sucesión de números naturales donde todo elemento es la suma de los dos que le preceden: 1, 2, 3, 5, 8, 13, etc.
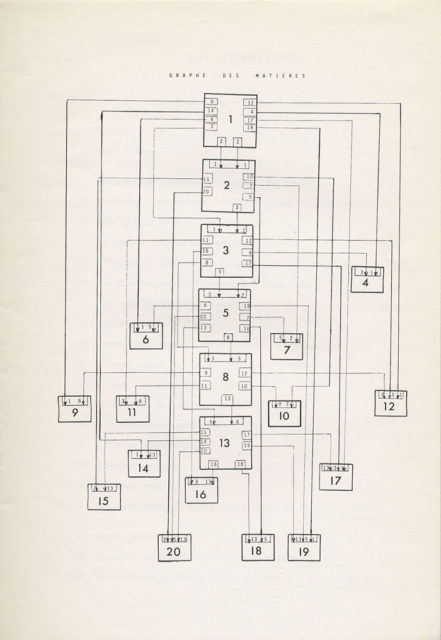
El teorema es el de Zeckendorf que permite representar todo entero natural como la suma de un cierto número de elementos de la sucesión de Fibonacci. Así, 9 = 8 + 1, 20 = 13 + 5 + 2, etc. Esto permite asociar a la sucesión de los veinte primeros enteros un grafo de dependencias que se reproduce a continuación.
La transferencia de la estructura matemática a la restricción literaria es de orden semántico: el contenido del poema en la posición n depende del contenido de los poemas cuyo puesto forma la representación “de Zeckendorf” de n.
Así, el poema número 20 depende del contenido de los poemas en la posición 13, 5 y 2. Observemos que una tal restricción, puramente semántica, lleva también a definir restricciones prosódicas.
Por supuesto, hemos añadido al sistema anterior algunas restricciones suplementarias que el lector descifrará sin esfuerzo.
Si entendéis francés, os recomiendo la lectura de este texto. Como la mayoría de los textos escritos bajo restricción oulipiana, se descubren los detalles tras varias lecturas, mirando en cada una de ellas diferentes aspectos del contenido o de la estructura. Además, Braffort incorpora en su poemario conceptos y personajes matemáticos. Es una auténtica delicia, un juego, un reto, un rompecabezas extraordinario que enlaza las matemáticas y la literatura.
Referencias
-
Maths and poetry, Futility Closet, 11 de enero de 2015.
-
Édouard Zeckendorf (1972). Représentation des nombres naturels par une somme de nombres de Fibonacci ou de nombres de Lucas. Bull. Soc. R. Sci. Liège 41: 179-182.
-
Paul Braffort (1979).Mes hypertropes. La Bibliothèque oulipienne vol. I, no. 9, Seghers
Notas:
iLa parte de la teoría de números que estudia conjuntos de enteros y su comportamiento bajo la suma.
iiPor ejemplo, 100 = 55 + 34 + 8 + 2 + 1 o 100 = 89 + 8 + 2 + 1.
iiiTraducido por la autora.
iv Se refiere a Jacques Roubaud (1932), matemático y miembro del grupo OuLiPo.
–
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
