Un tema que ya se está convirtiendo en clásico en la sección Matemoción del Cuaderno de Cultura Científica es la sucesión de Fibonacci. Ya que como decía Marta Macho en una de sus últimas entradas ¡Nos encanta Fibonacci!.
Como seguramente sabrán las personas que estén leyendo esta entrada, la conocida como sucesión de Fibonacci fue introducida por el matemático italiano Leonardo de Pisa (1170-1241), a quien se le conocía como Fibonacci, esto es, hijo de Bonaccio, en su libro “Liber Abaci” (1202, El libro del Ábaco), como solución a uno de los problemas de ingenio que se planteaban en el mismo.
Recordemos el problema en cuestión:
“Consideremos una familia de conejos con la característica de que tardan un mes en ser fértiles. Cuando han alcanzado la fertilidad, cada pareja se aparea teniendo al mes siguiente (cada hembra) una pareja de crías (un macho y una hembra) que de nuevo tardarán en ser fértiles un mes y entonces se aparearán. ¿Cuántas parejas de conejos habría al cabo de un tiempo dado, por ejemplo, un año?”
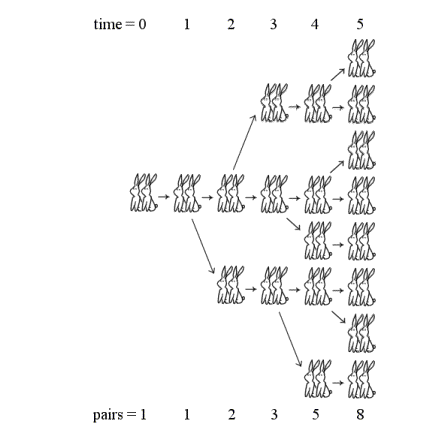
No es difícil darse cuenta que la sucesión de parejas de conejos, suponiendo que estos no se mueran, que hay cada mes es la siguiente:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
que tiene la propiedad de que cada número der la sucesión, Fn, es igual a la suma de los dos números anteriores, Fn = Fn – 1 + Fn – 2, para n = 1, 2, 3, …
En la sección Una de Mates del Cuaderno de Cultura Científica, que recoge los videos de esta sección dentro del programa de TV Orbita Laika, en su segunda temporada, podéis ver la explicación del problema de Fibonacci.
La sucesión de Fibonacci no solo es interesante dentro de las matemáticas, sino que juega un papel fundamental en el estudio de la morfología de las plantas, en concreto, en la filotaxis, siendo el número de espirales de las cabezas de los girasoles, las piñas o el romanescu, números de dicha sucesión, también nos la encontramos en el arte, como en las obras del artista italiano Mario Merz (1925-2003), o en la literatura, como en el poema Alfabeto (1981) de poeta danesa Inger Christensen (1935-2009).
Sin embargo, en esta entrada no vamos a hablar de las propiedades matemáticas de la sucesión de Fibonacci o de la presencia de esta en la naturaleza y la cultura, sino que vamos a viajar hasta la India, unos cuantos siglos antes de que el matemático italiano Fibonacci escribiera su libro Liber Abaci, para descubrir la presencia de los números de Fibonacci en la poesía en sánscrito.
En 1985, el matemático indio Parmanad Singh, del Raj Narain College de la India, publicó en la revista Historia Mathematica el artículo The so-called Fibonacci Numbers in Ancient and Medieval India (Los así llamados números de Fibonacci en la India antigua y medieval), en el cual mostraba el origen indio de los números de Fibonacci y su conexión con la poesía en la lengua sánscrita.
En la poesía en sánscrito, lengua antigua de la India, existen los poemas en los cuales hay un número fijo de sílabas por verso (los llamados varna-vrttas) y aquellos en los que hay un número fijo de “moras” por verso (llamados matra-vrattas). Para los que no sabíamos que es la “mora”, esta es “la unidad que mide el peso silábico, es decir, la duración de los segmentos fonológicos que componen la sílaba” (según la Wikipedia). En sánscrito hay dos tipos de sílabas, unas cortas (llamadas laghu), de una mora o instante silábico, y otras largas (llamadas guru), de dos moras.
El latín, como las lenguas clásicas indias, el sánscrito y el prácrito, o el griego, también constaba de dos tipos de sílabas, cortas y largas. Las sílabas podían tener una sola mora, como aquellas sílabas acabadas en vocal breve, ya que en latín se distinguía entre vocales breves y largas, y las que tenían dos moras, que eran el resto de sílabas, las terminadas en vocales largas o en consonante. Una misma palabra podía tener dos significados distintos en función de que la vocal fuese corta o larga, así la “a” de “mălus” era una vocal corta y la palabra significaba “malo”, mientras que en “mālus” la vocal era larga y el significado era “manzano”, o también “mástil”. La primera palabra tenía dos sílabas con tres moras, mientras que la segunda tenía dos sílabas con cuatro moras. Otro ejemplo de palabra con dos significados en función de si la vocal es corta o larga es “solum”, con vocal corta “sŏlum” significaba “suelo”, mientras que tenía el significado de “solo” con la vocal larga, “sōlum”.
Volviendo al sánscrito, un verso de tipo varna-vrttas, que recordemos que en este tipo de métrica se mantiene el número de sílabas de cada verso, con tres sílabas posee 8 posibilidades, en relación a las moras que componen el mismo. Si llamamos C a una sílaba corta, con una mora, y L a una sílaba larga, con dos moras, las posibles estructuras, en relación a las moras, son 8: CCC, LCC, CLC, CCL, CLL, LCL, LLC y LLL. Aunque el número de sílabas se mantiene constante, el número de moras varía de unas estructuras a otras, la primera tiene 3 moras, las tres siguientes 4 moras, las tres con dos silabas largas tienen 5 moras y la última tiene 6 moras.
Sin embargo, si consideramos un verso de tipo matra-vrttas, que recordemos que en este tipo de métrica se mantiene el número de moras de cada verso, con tres moras, existen solamente 3 estructuras posibles CCC, CL y LC, siendo ahora variable el número de sílabas, la primera con tres sílabas y las otras con dos.
Pero… ¿qué tienen que ver los poemas en sánscrito con los números de Fibonacci?
Para dar respuesta a esta pregunta vamos a centrarnos en la métrica matra-vrttas. Veamos cuántas posibles estructuras existen de versos con 1, 2, 3, 4 o 5 moras.
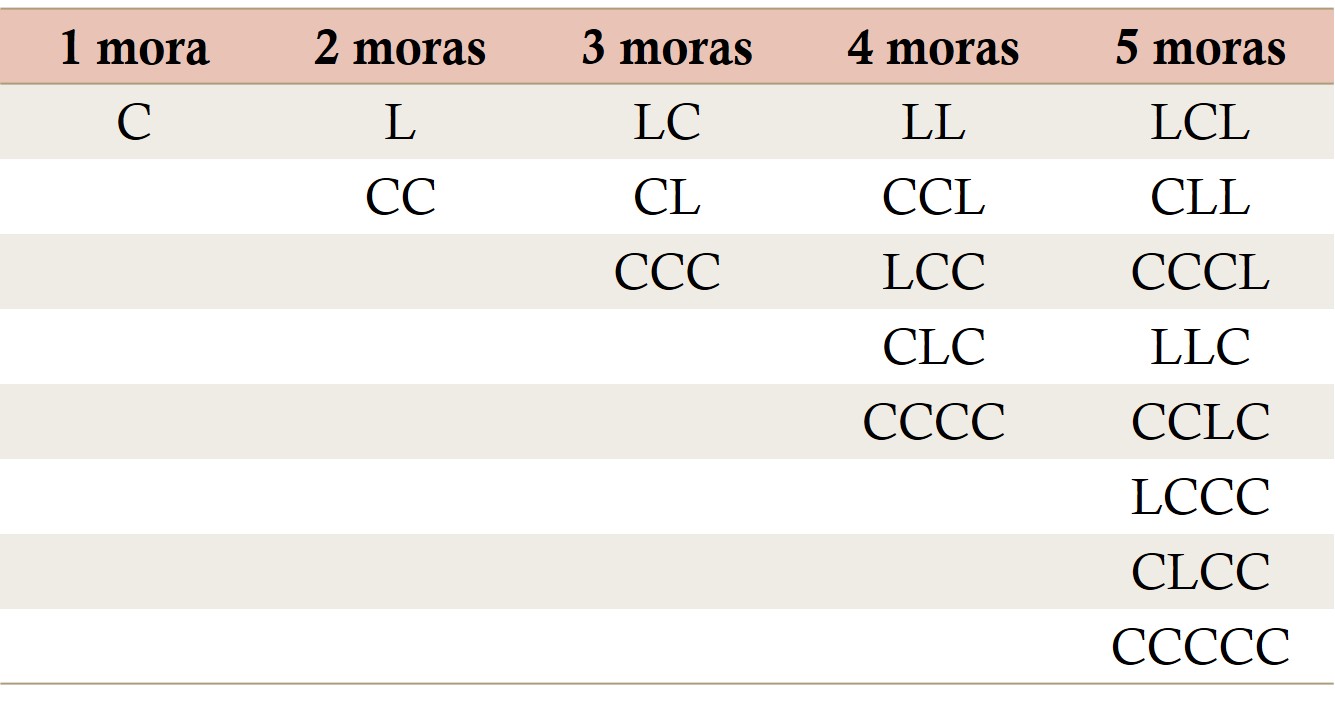
El número de variaciones posibles, para versos con 1, 2, 3, 4 o 5 moras, son 1, 2, 3, 5 y 8, que como podemos observar son números de Fibonacci. Pero fijémonos, por ejemplo, en las estructuras de los versos con 4 moras, los podemos dividir en dos tipos, los que terminan en una sílaba larga (L), que son las dos estructuras con 2 moras (L y CC) a las que se ha añadido dos moras mediante una sílaba larga (LL y CCL), y los que terminan en una sílaba corta (C), que son las tres estructuras con 3 moras (LC, CL y CCC) a las que se ha añadido una mora mediante una sílaba corta (LCC, CLC y CCCC). En consecuencia, hay 2 + 3 = 5 posibles estructuras con 4 moras.
Si ahora quisiéramos ver cuántas estructuras diferentes existen para los versos de la métrica matra-vrttas con 6 moras, obtendremos que son 13, los generados a partir de los de 4 moras al añadirle una sílaba larga (L), que son 5, y los generados a partir de los de 5 moras al añadirles una sílaba corta (C), que son 8, luego en total 5 + 8 = 13. En concreto, LLL, CCLL, LCCL, CLCL y CCCCL, junto con LCLC, CLLC, CCCLC, LLCC, CCLCC, LCCCC, CLCCC y CCCCCC.
Por lo tanto, lo que estamos diciendo es que el número de estructuras posibles con m moras es igual a la suma del número de estructuras con m – 1 y m – 2 moras, que es el motivo por el que salen los números de Fibonacci. En resumen,
¡¡la cantidad de estructuras posibles para versos matra-vrttas con m moras es igual al número de Fibonacci Fm+1!!
Si tenemos en cuenta que una sílaba corta (C) es 1 tiempo y una sílaba larga (L) son 2 tiempos, podemos escribir el anterior resultado como un resultado matemático.
Teorema: El número de Fibonacci Fm+1 es igual al número de formas de obtener el número m como sumas de 1s y 2s, donde el orden sí importa.
Por ejemplo, arriba hemos visto que el número 4 se puede obtener como cinco sumas diferentes con 1s y 2s, a saber, 2 + 2, 1 + 1 + 2, 2 + 1 + 1, 1 + 2 + 1 y 1 + 1 + 1 + 1, siguiendo el orden del cuadro anterior.
Ya hemos visto la relación que tiene la poesía en sánscrito con los números de Fibonacci, pero la pregunta ahora es si en la India eran conscientes de esta relación. Veamos lo que nos dice Parmanand Singh en su artículo.
Según este autor, Acarya Pingala (que vivió entre el 700 a.c. y el 100 d.c.), quien fue la primera autoridad en el estudio de la métrica en la India, pudo tener conocimiento de estos números, los conocidos como números de Fibonacci. Sin embargo, no existe una evidencia directa de esto, sino que en los comentarios de su obra realizados en el siglo X por el comentador Yadava, este habla de la regla de Pingala “misrau ca” (algo así como “y los dos juntos”) para explicar la expansión de los matra-vrttas combinando las expansiones de las dos métricas anteriores al añadir un guru (L) y un laghu (C), respectivamente. Y algo similar ocurre con otra autoridad antigua en la métrica de la India, Acarya Bharata, quien pudo vivir entre el 100 a.c. y el 350 d.c.
Sin embargo, la primera autoridad en el estudio de la métrica en la India que menciona explícitamente la regla de la formación de los números de variaciones de matra-vrttas fue Acarya Virahanka, quien vivió entre los siglos sexto y octavo. Puede leerse en una de sus obras algo así “Juntando las variaciones de las dos métricas anteriores, se obtiene la cantidad. Este es un método para conocer el número (de variaciones) de la siguiente matra-vrtta”.
Y el primer autor que menciona explícitamente los números de Fibonacci, mientras analiza y comenta la obra de Acarya Virahanka, es Gopala, cuyo comentario manuscrito de la obra del anterior está datado entre los años 1133 y 1135.
Otra autoridad que menciona explícitamente la regla de la creación de los matra-vrttas y los números de Fibonacci fue el poeta y estudioso de la métrica Acarya Hemacandra, en su estudio sobre la métrica Chandonusasana (1150). La regla de Hemacandra puede ser traducida algo así “la suma de los números [de variaciones] del último y anteúltimo, da lugar al del siguiente matra-vrtta”, y explícitamente menciona, como lo hizo Gopala, “1, 2, 3, 5, 8, 13, 21, 34 y se continua de esta forma”.
Parmanand Singh menciona otra obra famosa sobre la métrica en la cual se dan algunas reglas sobre los números de Fibonacci, Prakrta Paingala, publicada posiblemente en el siglo XIV.
Todos estos estudios sobre la métrica de los matra-vrttas pertenecen al campo de la ciencia de la métrica, pero el primer estudio matemático en India de la sucesión de Fibonacci fue la obra Ganita Kaumudi (1356) del matemático Narayana Pandita, posterior a la obra del matemático italiano Fibonacci. En esta obra se estudian más sucesiones de números, además de la de Fibonacci, como la conocida como sucesión de las vacas de Narayana, de la que hablamos en la entrada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci.
Bibliografía
1.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.
2.- Parmanad Singh, The so-called Fibonacci Numbers in Ancient and Medieval India, Historia Mathematica 12, n. 3, p. 229 – 244 (1985).
3.- Página web del artista Rafael Araujo.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Lo Mejor de la Semana (1 – 7 de abril) | Hablando de Ciencia
[…] El origen poético de los números de Fibonacci se remonta a la India, varios siglos antes de que el matemático italiano los presentara en su libro Liber Abaci de 1202. […]
El árbol de Fibonacci — Cuaderno de Cultura Científica
[…] sucesión de Fibonacci fue introducida, al menos en Europa (en la entrada El origen poético de los números de Fibonacci puede leerse cómo surgió el conocimiento de esta sucesión en la India, en relación con la […]