En octubre de 2002, el compositor minimalista norteamericano Tom Johnson visitó la Universidad del País Vasco/Euskal Herriko Unibertsitatea. Durante dicha visita Tom Johnson ofreció dos interesantes seminarios sobre su forma de componer utilizando las matemáticas y se organizaron algunos conciertos. Una de las composiciones musicales que tuve el placer de escuchar entonces fue Las vacas de Narayana (1989), interpretada por los miembros del grupo Kuraia Ensemble (Asociación de Música Contemporánea del País Vasco), Andrea Cazzaniga (violín), Rafael Climent (clarinete) e Iñigo Ibaibarriaga (saxofón).

Para componer la obra Las vacas de Narayama, Tom Johnson se basó en el problema homónimo propuesto por el matemático indio Narayana Pandita (1340-1400) en su tratado de aritmética Ganita Kaumudi (1356). Una de las cuestiones estudiadas por Narayana Pandita en esta obra fueron las sucesiones que él llamó “aditivas”, entre las que se encuentra la que nosotros conocemos como sucesión de Fibonacci.

El problema de las vacas de Narayana dice lo siguiente:

Si las vacas tienen una cría cada año, y cada ternera, después de los tres años que necesita para convertirse en una vaca madura, tiene una cría a principio de cada año, ¿cuántas vacas habrá después de 20 años a partir de una primera ternera?

Si empezamos con una ternera recién nacida, a principios de año, durante los tres primeros años solamente tendremos una (1) vaca, esa primera ternera. El cuarto año empezará realmente a crecer la población bovina, con la vaca inicial y su primera ternera, luego dos (2) vacas en total. Habrá una ternera más al principio de cada uno de los dos siguientes años, luego tres (3) el quinto año y cuatro (4) el sexto. Al inicio del séptimo, la primera ternera nacida de la vaca original ya puede tener también terneras, por lo que ese año habrá dos vacas adultas y cuatro terneras, en total, seis (6) vacas. El siguiente año una nueva ternera pasa a la madurez y tres vacas tienen una ternera cada una, luego en total hay tres vacas maduras y seis terneras, luego nueve (9) vacas. Al inicio del noveno año, habrá trece (13) vacas, cuatro adultas y nueve terneras. En el siguiente gráfico hemos representado la evolución de vacas en esos nueve primeros años.

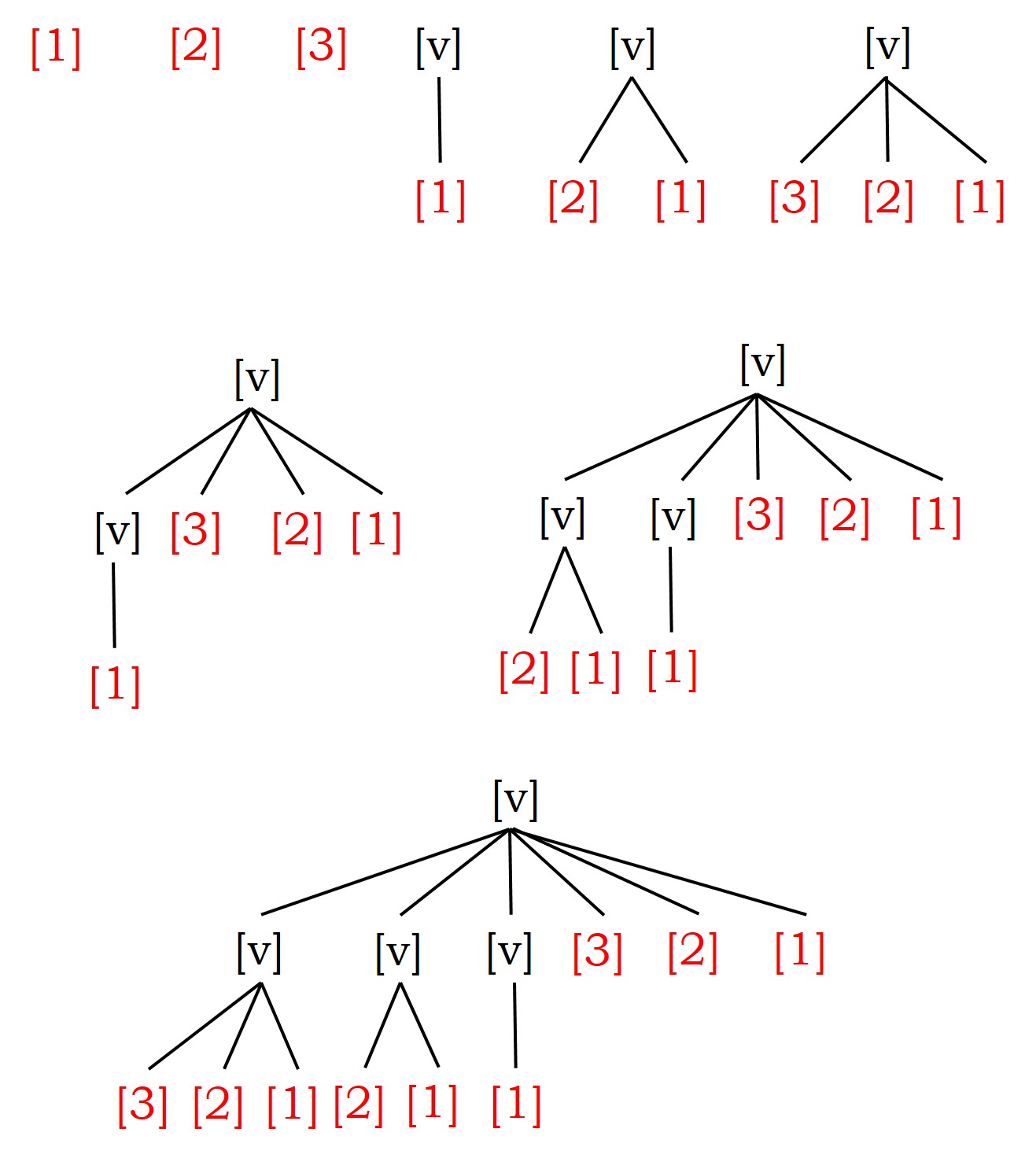
Pero continuemos… ¿cuántas vacas habrá el décimo año? Estarán las que ya estaban el año anterior, es decir, trece (13) vacas, más las terneras de las vacas que ese año pueden tener crías, que son exactamente las vacas que había hace tres años, seis (6) vacas, en total, diecinueve (13 + 6 = 19) vacas. Como se ve en el siguiente gráfico, seis son vacas maduras y trece son terneras, pero también podemos numerarlas por generaciones, la vaca original es la primera generación, hay siete vacas de la segunda generación, diez de la tercera y una de la cuarta.

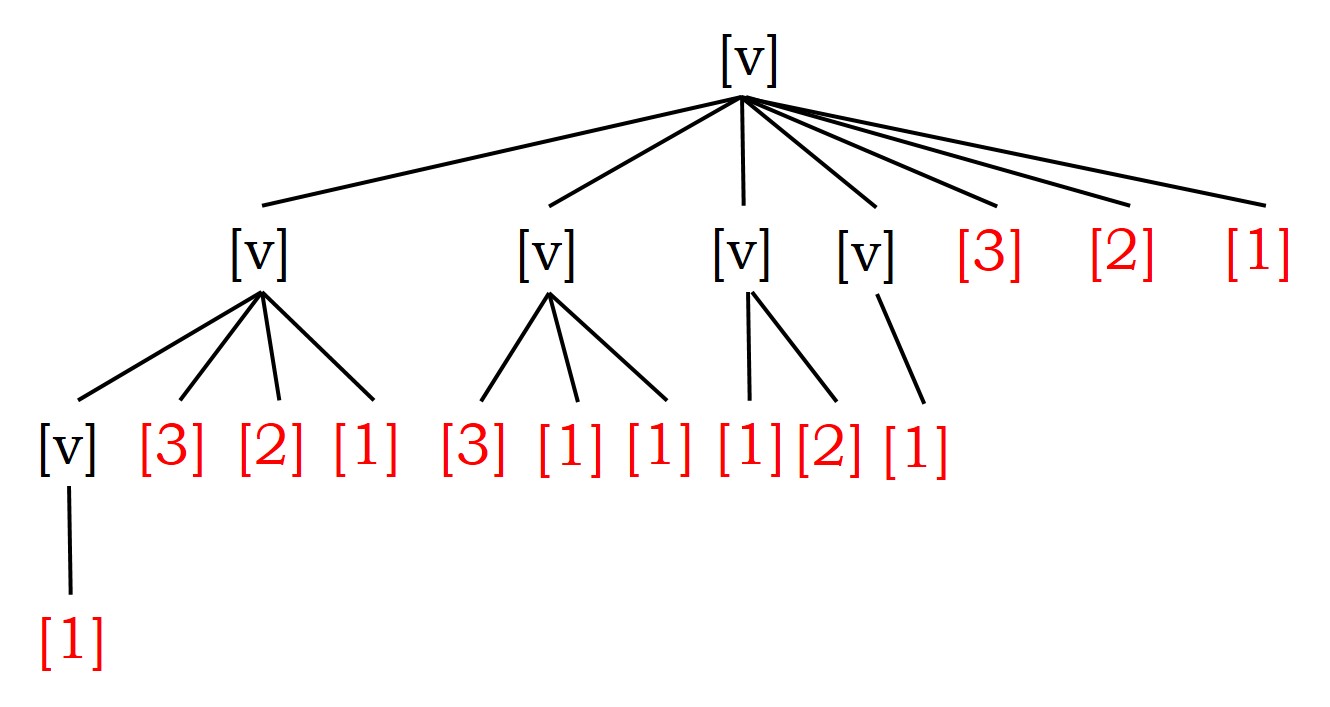
El razonamiento que hemos realizado para obtener el número de vacas al inicio del décimo año es, de hecho, general y realmente nos da una fórmula recursiva para resolver el problema de las vacas de Narayana. Si se denota por v(n) el número de vacas que habrá en el año n, entonces

v(n) = v(n – 1) + v(n – 3),

siendo además, v(1) = v(2) = v(3) = 1.

Por lo tanto, se pueden obtener fácilmente los primeros veinte números de la sucesión de vacas de Narayana,

1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595, 872, …

Luego, después de veinte años, es decir, al inicio del año veintiuno, habrá 406 + 872 =1.278 vacas.

Incluso, podemos hacer una tabla de la sucesión de vacas de Narayana, viendo las vacas que hay de cada generación.

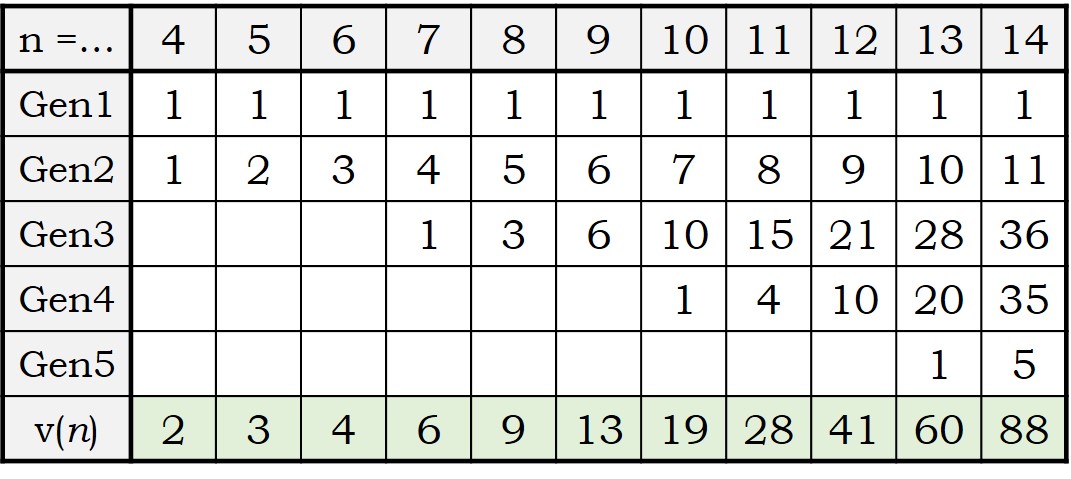
Observando esta tabla con los primeros años ya podemos extraer algunas curiosas conclusiones. Por ejemplo, el número de vacas de la segunda generación son los números naturales, puesto que son las vacas que van naciendo de la vaca original, y cada año tiene una nueva ternera, luego cada año una más, 1, 2, 3, 4, 5, …

En la tercera generación se obtienen los números triangulares, ya que son las sumas de los primeros números naturales, puesto que son las vacas descendientes de las de la generación anterior. Por ejemplo, en el décimo año hemos visto que el número de vacas de la segunda generación eran 1 + 2 + 3 + 4 = 10. Recordemos que los números triangulares T(n), que se llaman así puesto que son los que se obtienen al colocar piedras o discos circulares formando un triángulo equilátero (como se ve en la imagen siguiente), son aquellos que son la suma de los primeros números naturales, T(n) = 1 + 2 + 3 + … + (n – 1) + n.

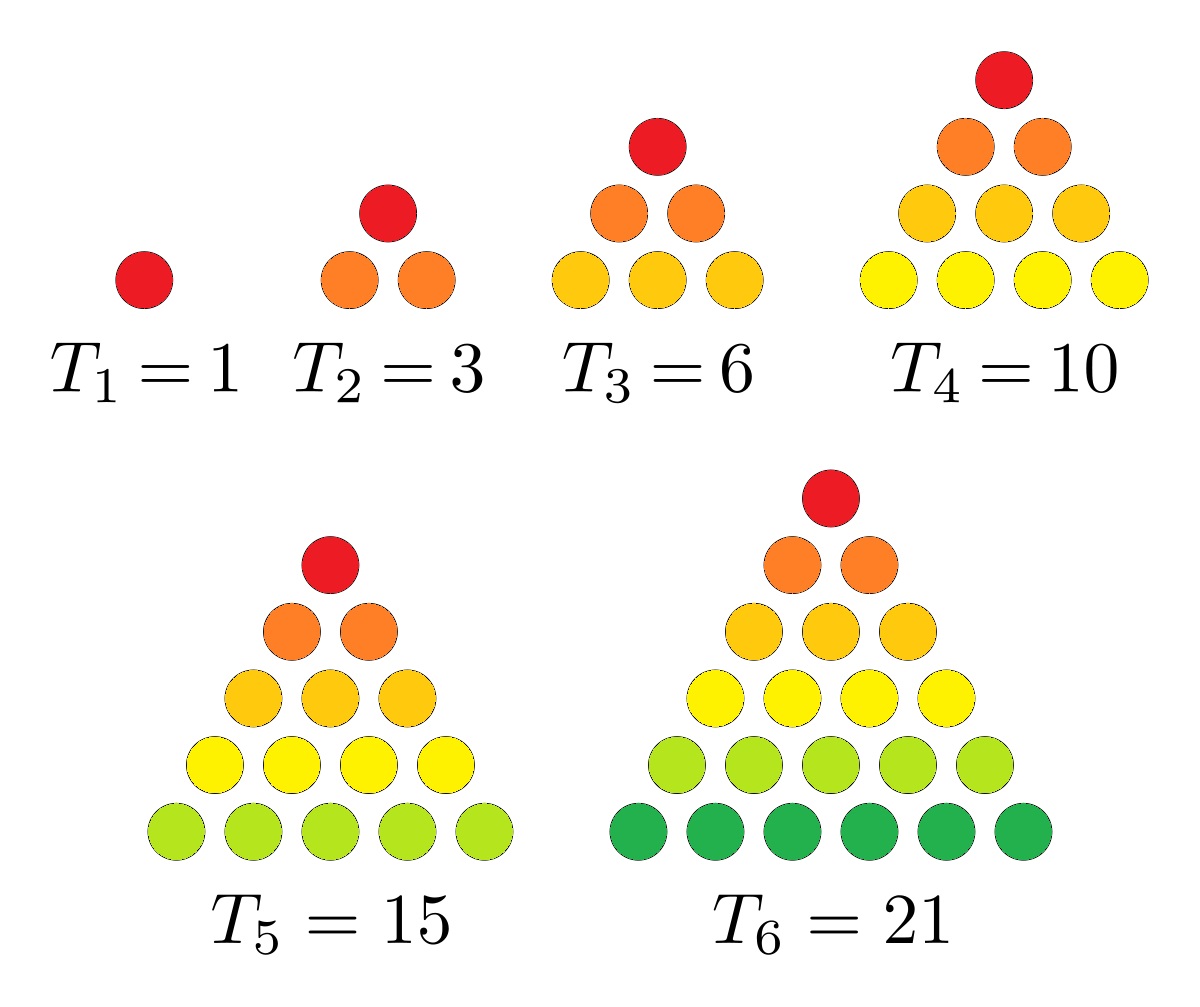
Por el mismo motivo, las vacas de la cuarta generación serán los llamados números tetraédricos, 1, 4, 10, 20, 35, … ya que serán las sumas de los primeros números triangulares, los que aparecen en la tercera generación. Recordemos que los números tetraédricos son el número de bolas que hay en una pirámide triangular (como la de la imagen), es decir, un tetraedro, y que es igual a la suma de los primeros números triangulares, TT(n) = T(1) + T(2) + … + T(n).

Dejemos por un momento la sucesión de las vacas de Narayana y volvamos a la composición musical basada en este problema. Pero antes presentemos brevemente a su autor, el compositor Tom Johnson.

Tom Johnson (Greeley, Colorado, EE.UU.), es un compositor minimalista y teórico de la música estadounidense. Se graduó en la Universidad de Yale, donde obtuvo además su grado avanzado en música. Fue alumno del compositor Morton Feldman (1926-1987), uno de los artífices, junto con John Cage (1912-1992), de la música aleatoria.

Es un compositor minimalista, ya que trabaja con formas simples, escalas limitadas y de manera general, con material reducido. Y dentro del minimalismo destaca por el uso de las matemáticas en el proceso creativo. Fórmulas matemáticas, trigonometría, simetrías, teselaciones, combinatoria, sucesiones de números enteros, teoría de números o fractales, son algunas de las teorías matemáticas que utiliza en sus composiciones.

Tom Johnson ha escrito de su música: “quiero encontrar la música, no componerla”, o como decía su maestro Morton Feldman “Deja a la música hacer lo que quiere hacer”. Mientras John Cage, o Morton Feldman, realizan esta búsqueda mediante el azar, Tom Johnson lo hace mediante las matemáticas.

Entre sus obras encontramos óperas como Riemannoper (1988), Trigonometría (1997) o la más famosa La ópera de las cuatro notas (1972), que fue representada en España en 2015 por Vania Produccions bajo la dirección de Paco Mir (que muchos conoceréis por ser uno de los miembros del trío Tricicle) o composiciones musicales muy creativas e interesantes, como Nueve campanas (1973), Simetrías (1981), Melodías Racionales (1982), Melodías infinitas (1986), Música para 88 (1988), Las vacas de Narayana (1889), Galileo (2001), Mosaicos (2002), o Ritmos de Vermont (2008), entre muchas otras.

Ha escrito libros como la colección de artículos de crítica musical The voice of the new music (Apollohuis, 1989), Self-similar Melodies (Editions 75, 1996) o Looking at numbers (Birkhauser, 2014).

En la composición musical Las vacas de Narayana, Tom Johnson realiza en esta obra una demostración musical del problema matemático. Para ello, divide la pieza en diferentes partes, cada una de las cuales se corresponde con un año del problema de las vacas, y en cada una de esas piezas hay tantas notas como el número de vacas que hay ese año, siendo una nota larga para cada vaca madura y una nota corta para cada ternera.

Aunque antes de seguir hablando de esta composición, lo que debemos hacer es escucharla. Esta pieza está incluida en el álbum Kentzy plays Johnson (2004), con el saxofonista Daniel Kientzy y en el álbum Cows, Chords and Combinations (2011), del grupo Ensemble Klang. Os traemos aquí dos conciertos que están en youtube. Uno es un concierto en Toronto en 2010, organizado por Continuum Contemporary Music.

mientras que el otro es un concierto en 2014, en el Switchboard Music Festival

Como hemos podido observar los conciertos empiezan en el cuarto año, cuando la vaca original tiene su primera ternera. Además, Tom Johnson distribuye las notas largas y cortas, que se corresponden con vacas maduras y terneras en la composición, siguiendo unas estructuras de árbol similares a los que hemos incluido más arriba para los diez primeros años del problema, y leyendo las vacas que hay, de arriba hacia abajo y de derecha a izquierda en esos diagramas de tipo árbol.

Por ejemplo, si escuchamos (o leemos la partitura, cuya primera página hemos incluido más abajo) la sucesión de notas que se corresponde con el quinto año del concierto (el octavo en el problema entero de las vacas de Narayana, o también en la partitura escrita) y miramos al diagrama de árbol de ese año, observaremos que las notas serán

larga – corta – corta – corta – larga – corta – larga – corta – corta

Cuando se escucha la obra de Tom Johnson, los primeros años de la composición musical sirven para entender el problema de las vacas de Narayana y la forma en la que el compositor asocia las notas musicales con las vacas maduras y crías, mientras que según van pasando los años vamos percibiendo la estructura, que surge a partir del problema matemático, de la composición musical.

Regresemos de nuevo a las matemáticas de la sucesión numérica de las vacas de Narayana. Es un hecho muy conocido, tanto en la literatura matemática, como por las personas interesadas en la sucesión de Fibonacci (véase alguno de los libros titulados La proporción áurea, de Mario Livio o Fernando Corbalán), que si se toma el cociente entre dos miembros consecutivos de la sucesión de Fibonacci F(n + 1) / F(n), esta sucesión de cocientes, converge (al ir aumentando n) a la proporción áurea, phi = 1,6180339…

1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 = 1,666…; 8/5 = 1,6; 13/8 = 1,625; 21/13 = 1,615…; 34/21 = 1,619…; 55/33 = 1,617…; etc…

¿Ocurrirá algo similar si tomamos la sucesión de los cocientes de números consecutivos de la sucesión de las vacas de Narayana? La respuesta es afirmativa, como vamos a ver a continuación.

Empezamos en la fórmula recursiva de la sucesión de vacas de Narayana

v(n + 1) = v(n) + v(n – 2),

a la que le dividimos por v(n) y además, en el último sumando, multiplicamos y dividimos por v(n – 1), para obtener la expresión

v(n + 1) / v(n) = 1 + v(n – 2) / v(n – 1) × v(n – 1) / v(n).

Si llamamos κ al límite, cuando n tiene de infinito, del cociente v(n + 1) / v(n), la anterior expresión nos dice que κ satisface la ecuación de tercer grado κ ³ – κ ² – 1 = 0, que podemos llamar la ecuación de Narayana. Esta ecuación tiene tres soluciones, dos de ellas imaginarias, y la solución real que buscamos es (calculada con WolframAlfa)

Aproximadamente, κ = 1,46557123187676802665673… que podríamos llamar la proporción de Narayana.

Vamos a terminar esta entrada del Cuaderno de Cultura Científica mostrando algunas caracterizaciones interesantes de la sucesión de vacas de Narayana.

A. Número de embaldosados con triominós rectos de rectángulos 3 × (n – 1).

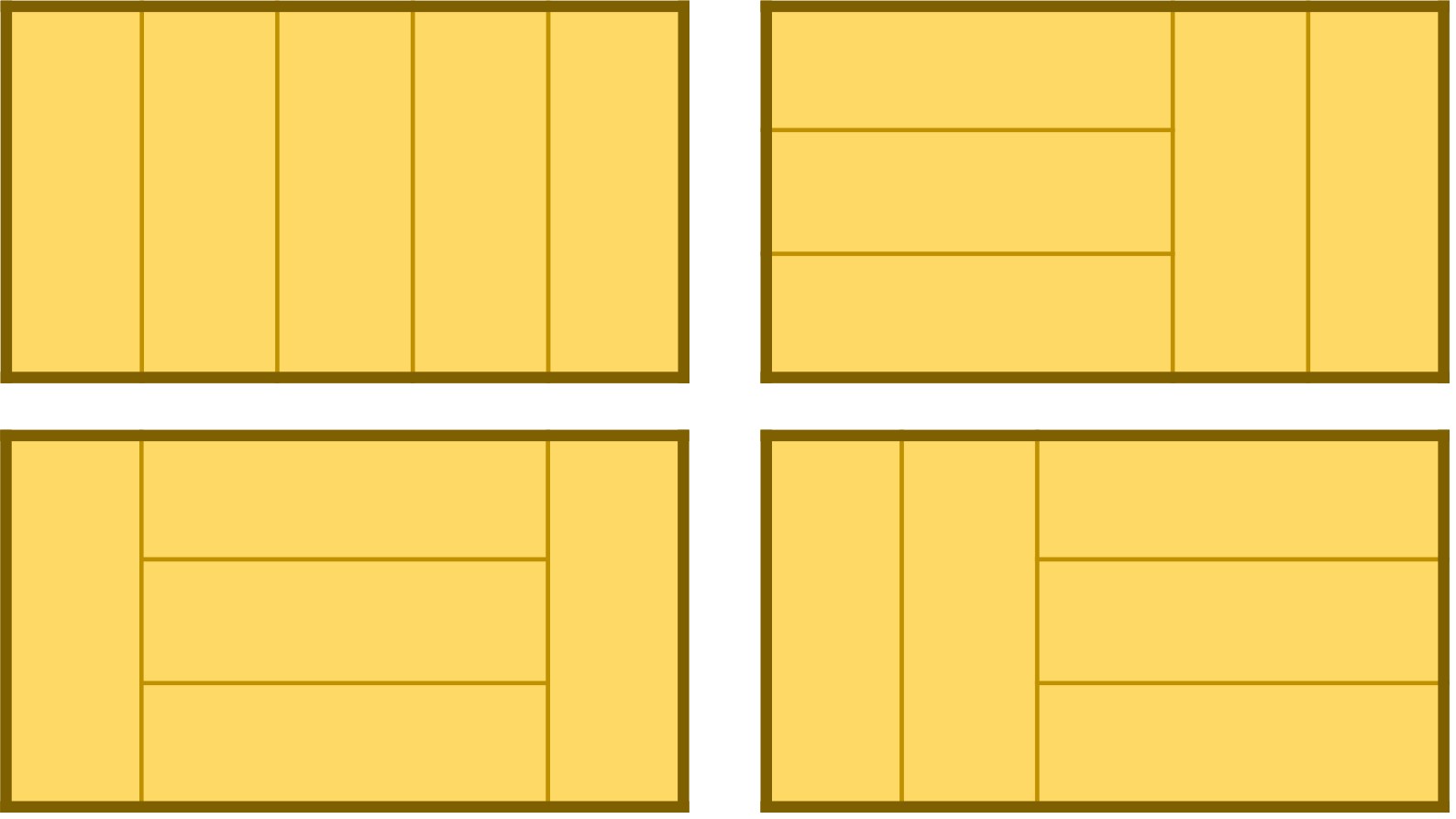
Consideremos un rectángulo de tamaño 3 × (n – 1), como el que aparece en la imagen de abajo (ese en particular es de tamaño 3 × 5), entonces el número v(n) de la sucesión de vacas de Narayana para el año n, es igual a la cantidad de embaldosados posibles con triominós rectos, fichas de tamaño 1 × 3, también llamados I-triominós (véase la entrada Embaldosados con L-triominós (un ejemplo de demostración por inducción) [https://culturacientifica.com/2014/07/16/embaldosando-con-l-triominos-un-ejemplo-de-demostracion-por-induccion/]), es decir, el número de diferentes maneras que hay de colocar triominós rectos en el rectángulo 3 × (n – 1).

Esta caracterización es una versión geométrica del siguiente resultado de la Teoría de números relacionado con las particiones de los números.

B. Número de composiciones del número n – 1, con el 1 y el 3.

Recordemos primero dos conceptos básicos de la Teoría de números, como son las particiones y las composiciones. Una partición de un número entero positivo es una forma de expresarlo como suma de números enteros positivos, donde el orden no es relevante. Por ejemplo, el número 3 puede expresarse como suma de tres formas distintas {1 + 1 + 1, 2 + 1, 3}, mientras que existen cinco particiones del número 4 {1 + 1 + 1 + 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4}. Si se denota por p(n) el número de particiones de n, entonces p(3) = 3 y p(4) = 5.

Si en las particiones se tuviera en cuenta el orden, se obtendrían las composiciones, o particiones ordenadas, que se denotan c(n). Así, las particiones ordenadas de 4 son: {1 + 1 + 1 + 1, 2 + 1 + 1, 1 + 2+ 1, 1 + 1 + 2, 2 + 2, 3 + 1, 1 + 3, 4}. Luego, c(4) = 8, mientras que p(4) = 5.

La sucesión de números de Narayama, al igual que la de Fibonacci (véase, por ejemplo, el libro Cayley, el origen del álgebra moderna), se puede relacionar con ciertos tipos de composiciones de números. En particular, la anterior caracterización geométrica es equivalente a que el número v(n) de la sucesión de vacas de Narayana para el año n, es igual al número de composiciones del número n – 1 con únicamente los números 1 y 3. Así, como las composiciones, con 1 y 3, de 6 son {1+1+1+1+1+1, 1+1+1+3, 1+1+3+1, 1+3+1+1, 3+1+1+1, 3+3}, entonces v(7) = 6.

C. Número de formas de colocar n – 2 alfombras tatami en una habitación de tamaño 2 × (n – 2), sin que los vértices de 4 alfombras coincidan.

Recordemos que las alfombras tatami de las casas tradicionales japonesas tienen una relación de tamaño de 1 × 2.

Existen 13 formas de cubrir una habitación de tamaño 2 × 7 con alfombras tatami, sin que coincidan las esquinas de cuatro de ellas, que es exactamente el número v(9). De hecho, esas 13 maneras pueden describirse de la forma 1111111, 111112, 111121, 111211, 112111, 121111, 211111, 11212, 12112, 21112, 12121, 21121, 21211.

Si lo pensamos un momento, la descripción con 1 y 2 de colocar las alfombras tatami (1 para las verticales, 2 para las horizontales) nos está diciendo realmente que podemos describir el número de la sucesión de vacas de Narayana v(n) como las composiciones de n – 2 con tan solo los números 1 y 2, pero sin que haya dos 2 juntos.

D. Número de composiciones del número n – 2, con el 1 y el 2, sin que haya dos 2 juntos.

Como despedida de esta entrada otra pieza del compositor minimalista norteamericano Tom Johnson, la primera de sus melodías racionales, en mi opinión una hermosa pieza, interpretada por el Gruppo di Musica Contemporanea Steffani, en el Conservatorio Steffani, de Castelfranco Veneto (Italia), en 2009.

Bibliografía

1.- Página web de Editions 75

2.- Tom Johnson, Kientzy plays Johnson (álbum), 2004.

3.- Jean-Paul Allouche, Tom Johnson, Narayana’s Cows and Delayed Morphisms, Cahiers du GREYC Troisiemes Journées d’Informatique Musicale (JIM 96) 4, p. 2-7, 1996.

4.- Parmanand Singh, The so-called Fibonacci Numbers in Ancient and Medieval India, Historia Mathematica 12, p. 229-244, 1985.

5.- Krishnamurthy Kirthi, Subhash Kak, The Narayana Universal Code, ArXiv, 2016.

6.- Tom Johnson, Self-Similar Melodies, Editions 75, 1996.

7.- Tom Johnson, Looking at numbers, Birkhäuser, 2014.

8.- Fernando Corbalán, La proporción áurea, El lenguaje matemático de la belleza, RBA, 2010.

9.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.

10.- Página web de la artista Charlotte Gerrard

11.- N. J. A. Sloane, La sucesión de vacas de Narayana, A000930 [https://oeis.org/A000930], Enciclopedia on-line de sucesiones de números enteros.

12.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, colección Genios de las matemáticas, RBA, 2017.

13.- Frank Ruskey, Jennifer Woodcock, Counting Fixed-Height Tatami Tilings, The Electronic Journal of Combinatorics 16, 2009.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica