En mi anterior entrada del Cuaderno de Cultura Científica, titulada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci , estuvimos hablando de una curiosa sucesión de números, la sucesión de las vacas de Narayana, y de cómo el compositor minimalista estadounidense Tom Johnson (Greeley, Colorado, EE.UU., 1939), la había utilizado para componer una obra musical de título homónimo.

En el proceso creativo de su música, Tom Johnson busca encontrar la belleza de una forma objetiva, alejándose de la subjetividad de la música romántica y expresionista, que lo hace a través de los sentimientos. El compositor minimalista utiliza las matemáticas, es decir, la simetría, la combinatoria, las sucesiones numéricas, los números binarios, las funciones matemáticas, los fractales o la geometría, en su búsqueda de una belleza musical objetiva.
Un ejemplo ilustrativo podría ser la pieza musical Tango, que Tom Johnson compuso en 1984 para el virtuoso pianista estadounidense Yvar Mikhashoff, y para la cual utilizó el concepto matemático de las permutaciones. Si se toman cinco objetos cualesquiera, ya sean cinco números o cinco notas, existen 120 formas diferentes de colocarlos en orden, es decir, 120 permutaciones de los mismos. En concreto, el factorial de 5, 5! = 5 × 4 × 3 × 2 × 1 = 120, como ya explicamos en las entradas Cuadrados latinos, matemáticas y arte abstracto y El problema matemático de las cartas extraviadas o en el video La combinatoria, de la sección Una de Mates, en el programa de TV2 Órbita Laika.
Por lo tanto, si se toman cinco notas, hay 120 permutaciones distintas de esas cinco notas. Como puede apreciarse en la imagen de la partitura que mostramos más abajo, las cinco notas de partida son [Re, Fa, Sol(#), La, Si(Ь)], y estas se van permutando [Re, Fa, Sol(#), Si(Ь), La], [Re, Fa, La, Sol(#), Si(Ь)], [Re, Fa, La, Si(Ь), Sol(#)], [Re, Fa, Si(Ь), Sol(#), La], [Re, Fa, Si(Ь), La, Sol(#)], y así hasta las 120 permutaciones que utiliza el compositor Tom Johnson para crear esta hermosa pieza, cuyo título es Tango, y que tiene un acompañamiento con ritmo argentino.

Pero lo mejor es que escuchéis el resultado. A continuación, dos versiones de la obra Tango. La primera es la interpretada por el pianista argentino Alberto Neuman
mientras que la segunda está interpretada con la estación de trabajo de audio digital Renoise,
Pero vayamos al tema de esta entrada del Cuaderno de Cultura Científica, las “teselaciones rítmicas perfectas”, un concepto matemático que ha sido introducido por el compositor Tom Johnson, mientras estudiaba algunos conceptos matemáticos para utilizarlos en la creación de nuevas piezas musicales.
Durante los años 2002 y 2003, Tom Johnson estuvo trabajando en lo que se conoce como teselaciones rítmicas, que son una traslación a dimensión uno, a la línea de tiempos musicales, del concepto clásico de teselación del plano o del espacio. Este trabajo dio lugar a su disco Tilework: 14 Pieces for 14 Solo Instruments (2003).
Pero el concepto de teselaciones rítmicas perfectas se le ocurrió a Tom Johnson intentando formular un equivalente en dimensión uno a lo que en matemáticas se conoce como las teselaciones perfectas del cuadrado o el problema de la cuadratura del cuadrado. Una teselación perfecta de un cuadrado es una teselación del cuadrado mediante cuadrados más pequeños, luego los cuadrados pequeños cubren el cuadrado original sin superponerse unos con otros, pero además con la condición de que todos los cuadrados de la teselación tengan diferentes tamaños.
La primera teselación perfecta de un cuadrado se obtuvo en 1938 por Cedric Smith, Arthur Stone, Leonard Brooks y William Tutte, conocidos como “Los cuatro de Trinity” (puede verse la historia de estos en la entrada Blanche Descartes y la cuadratura del cuadrado), utilizando para ello 69 cuadrados de diferentes tamaños. La teselación perfecta del cuadrado con menos cuadrados posibles, neceisita 21, y fue obtenida por A. J. Duijvestijn en 1978.
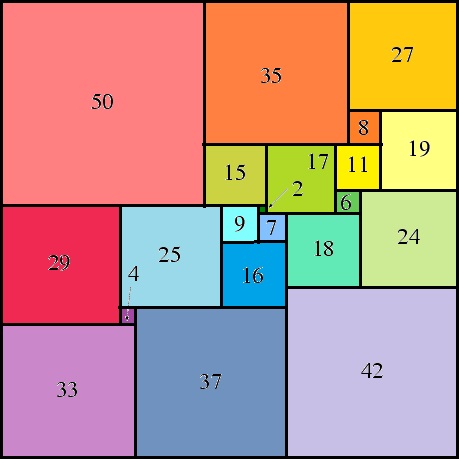
Tom Johnson propuso teselar, o rellenar, la línea de los números {0, 1, 2, … , m – 1, m} (pensemos en los tiempos musicales) con tríos de números que formen progresiones aritméticas (cada trío de números en progresión aritmética, es decir, de la forma a, a + r, a + 2r, como por ejemplo, 5, 7 y 9, son las baldosas de la teselación), de forma que entre todas esas progresiones aritméticas de tres números (las baldosas) llenen el espacio de la línea de los números, que no se superpongan, es decir, no haya números que estén en más de una progresión, y que cada progresión aritmética tenga una diferencia r, llamada “tempo” por Tom Johnson, diferente. El orden n de la teselación rítmica perfecta es el número de baldosas, esto es, progresiones aritméticas. Aquí el número de términos de cada progresión es tres, pero más adelante extenderemos la noción a progresiones aritméticas con más elementos, el índice.
Claramente, la cantidad de números que abarca una teselación rítmica perfecta de orden n (con índice 3) es 3n, desde 0 al 3n – 1.
La mejor manera de entender el concepto es mediante un ejemplo. Aquí mostramos el ejemplo que utiliza Tom Johnson, que es de orden 5 y que tesela los quince primeros números {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} mediante las siguientes teselas: (2, 3, 4), (8, 10, 12), (5, 9, 13), (1, 6, 11) y (0, 7, 14), cuyas diferencias son 1, 2, 4, 5 y 7, todas ellas distintas.
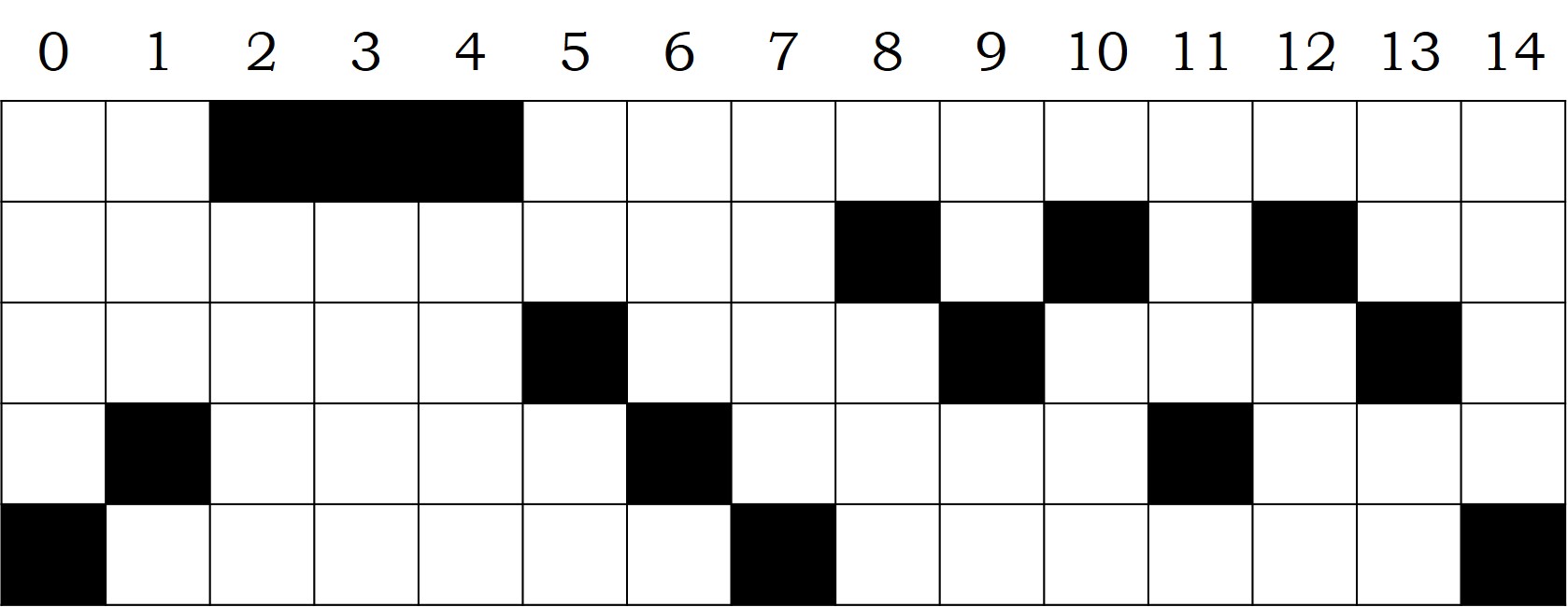
Utilizando esta teselación rítmica perfecta, con 5 teselas (tríos) diferentes y cuyos tempos (diferencias), de graves a agudos, son 7, 5, 4, 2 y 1, Tom Johnson compuso la pieza Tileworks for Piano (2003). La siguiente imagen que se ha extraído del libro Mathemusical Conversations, Mathematics and Computation in Music Performance and Composition (2016) explica, con la partitura original, el uso de esta teselación rítmica perfecta en la pieza.
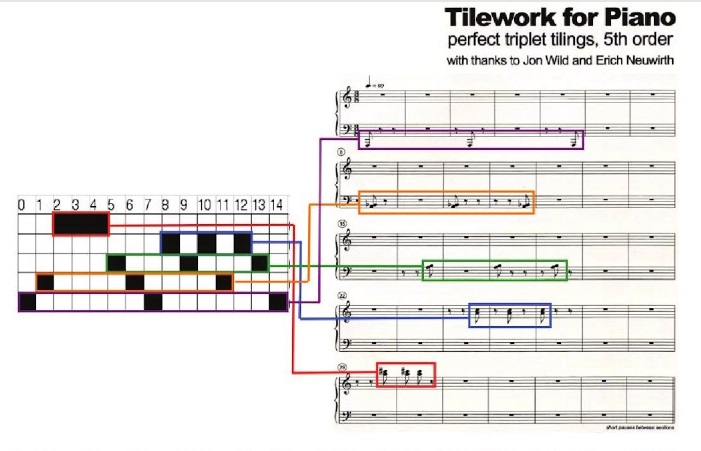
Pero escuchemos la pieza Tileworks for Piano compuesta por Tom Johnson, y que podemos encontrar en la página del compositor: Tileworks for Piano.
Como el propio compositor puso de manifiesto en el texto de la conferencia que impartió en 2004 en el Seminario MaMuX (Matemáticas, Música y relaciones con otras disciplinas), del IRCAM (Institut de Recherche et Coordination Acoustique/Musique), con el título Perfect Rhythmic Tilings, no existen teselaciones rítmicas perfectas de orden 2 (es decir, dos tríos que llenen seis tiempos, seis números), ni 3 (tres tríos que llenen 9 tiempos), ni 4 (cuatro tríos que teselen la línea de 12 números). Solo hay una de orden 5, que es la dada por Johnson, y su simétrica. Tampoco hay teselaciones rítmicas perfectas de orden 6. De orden 7, hay 9 soluciones, con sus simétricas, luego 18. Una de ellas la siguiente, cuyas diferencias son 1, 2, 4, 5, 7, 8 y 10.

En la Enciclopedia On-line se Sucesiones de Enteros aparece la sucesión A261516 del número de teselaciones rítmicas perfectas de {0, …, 3n – 1} con tríos (sucesiones aritméticas de tres números), en función del orden n, la cual empieza así
1, 0, 0, 0, 2, 0, 18, 66, 382, 1.104, 4.138, 15.324, 61.644, etc
Por ejemplo, hay 61.644 teselaciones rítmicas perfectas de orden 13 (sobre los primeros 39 números). Y se conoce hasta el orden 19.
De forma obvia, el concepto de teselaciones rítmicas perfectas se puede extender a progresiones aritméticas (baldosas) con cualquier número de elementos, no necesariamente tres. Por lo tanto, una teselación rítmica perfecta de orden n e índice k estaría dada por n progresiones aritméticas con k números cada una de ellas, a, a + d, a + 2d, …, a + kd, que cubren toda la línea de números {0, 1, 2, …, nk – 1}, que no se solapan, y tal que las diferencias d de las progresiones aritméticas son todas distintas.
En su texto Perfect Rhythmic Tilings, Tom Johnson estudió las teselaciones rítmicas perfectas con índices k = 2 y 3, es decir, con 2 y 3 números por progresión aritmética, pero dejó abierto el problema de la existencia de teselaciones rítmicas perfectas para k = 4. Afirmó que no existían tales teselaciones para órdenes menores, o iguales, que 7, pero quedaba abierto el problema para órdenes mayores.
Shalosh B. Ekhad (de quien ya hablamos en la entrada El extraño caso del matemático Shalosh B. Ekhad ) y Lara Pudwell resolvieron el problema planteado por Tom Johnson construyendo una teselación rítmica perfecta de índice 4 y orden 15, que es el orden más bajo posible para el índice 4, sobre los 60 primeros números. Es la siguiente…
[0, 16, 32, 48], [1, 3, 5, 7], [2, 13, 24, 35], [4, 22, 40, 58], [6, 21, 36, 51], [8, 14, 20, 26], [9, 10, 11, 12], [15, 29, 43, 57], [17, 25, 33, 41], [18, 30, 42, 54], [19, 23, 27, 31], [28, 37, 46, 55], [34, 39, 44, 49], [38, 45, 52, 59], [47, 50, 53, 56],
cuyas diferencias son 16, 2, 11, 18, 15, 6, 1, 14, 8, 12, 4, 9, 5, 7, 3.

Siguiendo los pasos de Tom Johnson, el compositor estadounidense Dean Rosenthal (Concord, Massachusetts, EE. UU., 1974) utiliza esta teselación rítmica perfecta, pero reordenando las diferencias de mayor a menor, para componer la pieza Perfecto para… violín (2011), que podéis escuchar, interpretada por la violinista y compositora Morgan Gerstmar, en la página de Dean Rosenthal.
Tras el ejemplo de Ekhad y Pudwell de teselación rítmica perfecta de índice 4, se han estudiado más en profundidad este tipo de teselaciones. Así, en la página Enciclopedia On-line se Sucesiones de Enteros aparece la sucesión A261517 del número de teselaciones rítmicas perfectas de {0, …, 4n – 1} con cuartetos (sucesiones aritméticas de cuatro números), en función del orden n, que es la siguiente (se conoce hasta el orden 23)
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 24, 38, 96, 444, 1.414, 5.134, 19.490
Para terminar esta entrada de la sección Matemoción del Cuaderno de Cultura Científica vamos a considerar un tipo especial de teselaciones rítmicas perfectas.
Dado el concepto de teselación rítmica perfecta de orden n e índice k, nos podríamos plantear si existen ejemplos de estas teselaciones pero con la propiedad de que las diferencias no solo sean diferentes, sino que sean todos los números entre 1 y n. A estas se las llama teselaciones rítmicas super perfectas.
Ninguno de los ejemplos de teselaciones rítmicas perfectas que hemos presentado hasta el momento son super perfectas. Por ejemplo, las diferencias del ejemplo de Tom Johnson son 1, 2, 4, 5 y 7, mientras que para que fuesen super perfectas deberían ser 1, 2, 3, 4 y 5.
Veamos un par de ejemplos. Una teselación rítmica super perfecta de índice 2, es decir, mediante pares de números, de orden 4, es (0, 4), (1, 3), (2, 5) y (6, 7).

Y un ejemplo, que encontramos en el artículo Perfect Rhythmic Tailings de Jean-Paul Davalan, con orden 9 e índice 3 (es decir mediante tríos de números) es (0, 6, 12), (1, 8, 15), (2, 11, 20), (3, 5, 7), (4, 9, 14), (10, 18, 26), (13, 16, 19), (17, 21, 25) y (22, 23, 24).

Las teselaciones rítmicas super perfectas ya existían en la literatura matemática, pero descritas desde otro punto de vista, bajo el nombre de sucesiones de Skolem (relacionadas también con las sucesiones de Langford).
Para explicar las sucesiones de Skolem, empecemos con el problema de los emparejamientos de Langford (para más información sobre el mismo puede consultarse el libro Del ajedrez a los grafos, La seriedad matemática de los juegos, que aparece en la bibliografía).
El origen de este juego se remonta a 1958, cuando el matemático escocés C. Dudley Langford publicó en la revista Mathematical Gazette el que es conocido como problema de los emparejamientos de Langford, o simplemente problema de Langford. En este artículo explicaba que viendo a su hijo pequeño jugar con un juguete de cubos de colores, dos de cada color, observó que había formado una torre de cubos, de tal forma que los dos cubos rojos estaban separados por un único cubo, los dos azules por dos cubos y había tres cubos entre los dos amarillos. Entonces se planteó si, añadiendo los dos cubos verdes podía mantener la propiedad anterior y que además hubiese una separación de cuatro cubos entre los dos verdes.
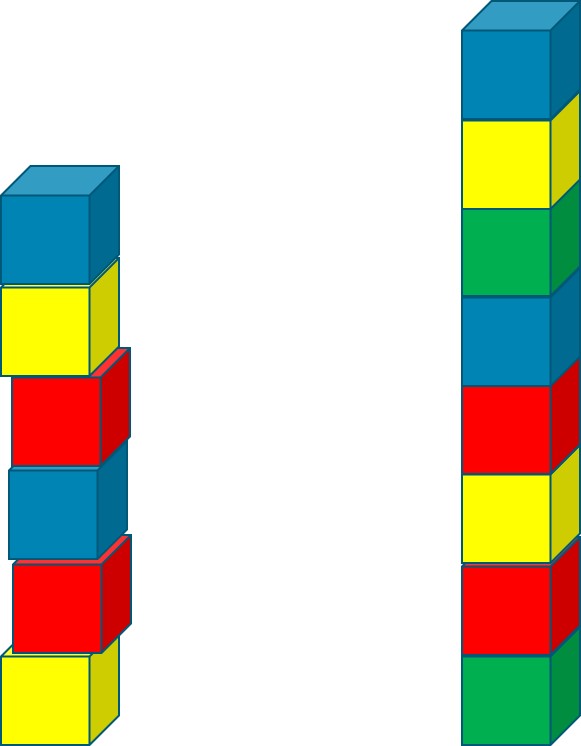
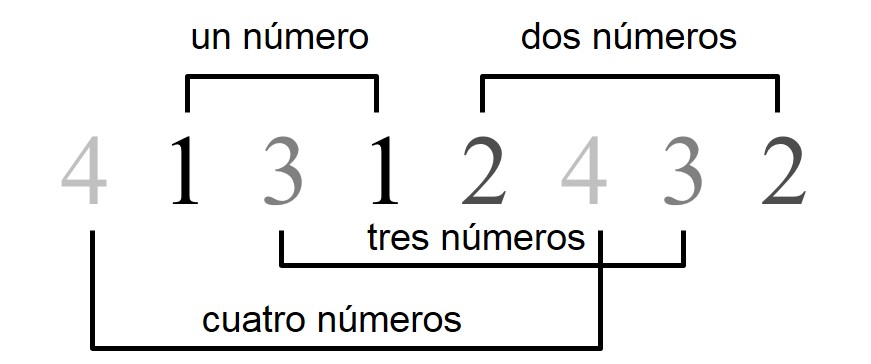
En su artículo, Langford reemplazó los cubos de colores por números y formuló el problema que lleva su nombre, en el que se plantea si es posible, y cómo, distribuir parejas de los números del 1 hasta n, de forma que entre los dos 1 haya un único número, entre los dos 2 haya dos, entre los dos 3 haya tres, así hasta los dos números n, entre los que habrá n números, es decir, si denotamos como ad la primera posición en la que aparece el número d (por ejemplo, contando desde la izquierda) y como bd la segunda, entonces
bd – ad = d + 1, para d = 1, 2, …, n.
A una tal distribución de los 2n números 1, 1, 2, 2, …, n, n se le llama sucesión de Langford. Por ejemplo, para n = 4 una solución es:
El problema de Langford, ya se formule con cubos de colores o con números, se puede extender a cualquier cantidad de cubos de colores o copias de cada número de 1 a n, así como el concepto de sucesión de Langford asociado, de tipo (k, n), es decir, con k copias de los números 1, 2, …, n. Por ejemplo, a continuación se muestra una sucesión de Langford de tipo (3, 9):

Mientras que C. Dudley Langford planteó este problema sobre la existencia de estas sucesiones numéricas en el contexto de la matemática recreativa, un problema similar surgió en 1957 en la investigación del matemático noruego T. H. Skolem sobre sistemas triples de Steiner, que son unos objetos matemáticos que pertenecen a la teoría del diseño combinatorio. Aunque en su investigación la condición matemática era que
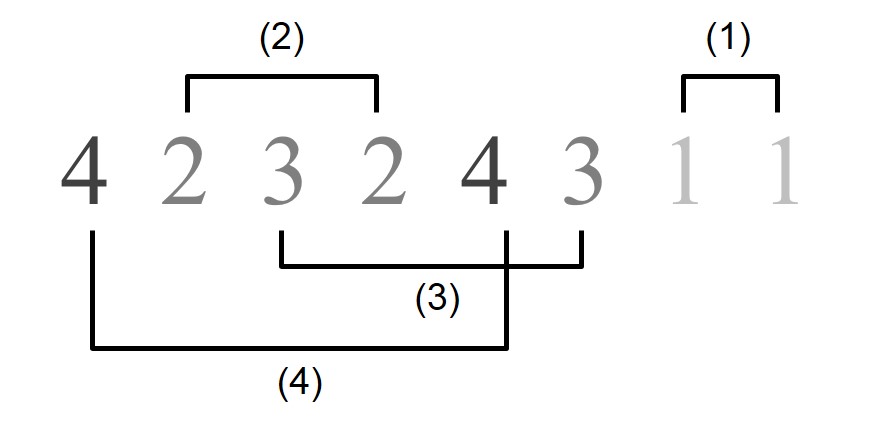
bd – ad = d, para d = 1, 2, …, n,
es decir, los dos números 1 están juntos, los dos 2 tienen un número entre ellos, hay dos posiciones entre los 3, y así para el resto.
Así un ejemplo de sucesión de Skolem para parejas de números, para n = 4, sería
Y un ejemplo para tríos, esto es, de sucesiones de Skolem de tipo (3, 9) sería:
6, 7, 9, 2, 5, 2, 6, 2, 7, 5, 8, 9, 6, 3, 5, 7, 3, 4, 8, 3, 9, 4, 1, 1, 1, 4, 8.
La condición de la sucesión de Skolem es realmente la misma que la de teselación rítmica super perfecta. Si tenemos una sucesión de Skolem de tipo (k, n), es decir, con n números distintos que se repiten k veces cada uno, tendremos una teselación rítmica super perfecta de la siguiente forma.
La línea de números que vamos a teselar son las nk posiciones de la sucesión de Skolem, empezando a contar desde la posición 0, es decir, desde 0 hasta nk – 1. Ahora, cada número de la sucesión de Skolem, que se repite k veces, va a ser una de las progresiones aritméticas de k números (nuestras baldosas), ya que la diferencia de los elementos de la progresión aritmética es d, la diferencia de las posiciones de cada dos números iguales (que además toma valores de 1 a n). Así, la sucesión de Skolem para pares de números anterior, 42324311, dará lugar a la teselación rítmica superperfecta (0, 4) –que son las posiciones del 4–, (1, 3) –que son las posiciones del 2–, (2, 5) –que son las posiciones del 3– y (6, 7) –que son las posiciones del 1–. De la misma forma, la sucesión de Skolem de tipo (3,9) anterior, no es más que la teselación rítmica super perfecta de orden 9 e índice 3, que hemos visto anteriormente.
Bibliografía
2.- Tom Johnson, Perfect Rhythmic Tilings, Lecture delivered at MaMuX meeting, IRCAM, 2004. Versión on-line en Editions75
3.- Tom Johnson, Tiling the Line in Theory and Practice, Lecture delivered at MaMuX meeting, IRCAM, 2002. Versión on-line en Editions75
4.- Tom Johnson, Tiling in my music, Perspectives in New Music 49, n. 2, p. 23-31, 2011.
5.- Jordan B L Smith, Elaine Chew, Gérard Assayag (editors), Mathemusical Conversations, Mathematics and Computation in Music Performance and Composition, (Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore 32), World Scientific, 2016.
6.- Jean-Paul Davalan, Perfect Rhythmic Tilings, Perspectives of New Music, vol. 49, n. 2, p. 144-197, 2011.
7.- Shaloh B. Ekhad, Lara Pudwell, A Perfect Rhythmic Tiling of Quadruplets, The Personal Journal of Shalosh B. Ekhad and Doron Zeilberger, 2004.
8.- Raúl Ibáñez, Del ajedrez a los grafos, La seriedad matemática de los juegos, colección El mundo es matemático, National Geographic, 2015.
9.- Tom Johnson, Looking at numbers, Birkhäuser, 2014.
10.- Exposición “Tom Johnson”, en Bains-Douches (d’Alençon, Francia), Febrero, 2018
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Los reptiles geométricos — Cuaderno de Cultura Científica
[…] se le ocurrió también el conocido problema de los emparejamientos de Langford (véase la entrada Teselaciones rítmicas perfectas o el libro Del ajedrez a los grafos, la seriedad matemática de los juegos), en un artículo […]