Para empezar esta entrada del Cuaderno de Cultura Científica os voy a proponer un juego. A continuación, vamos a mostrar dos listas. La primera lista, la situada a la izquierda, está formada por los nombres de cinco grandes artistas del siglo XX (Sonia Delaunay, Maruja Mallo, Lee Krasner, Georgia O’Keefe y Loïs Mailou Jones) y la lista de la derecha contiene los títulos de cinco obras de arte, una de cada una de las artistas de la primera lista. El juego consiste en unir cada una de las artistas de la fila de la izquierda con su correspondiente cuadro en la lista de la derecha.
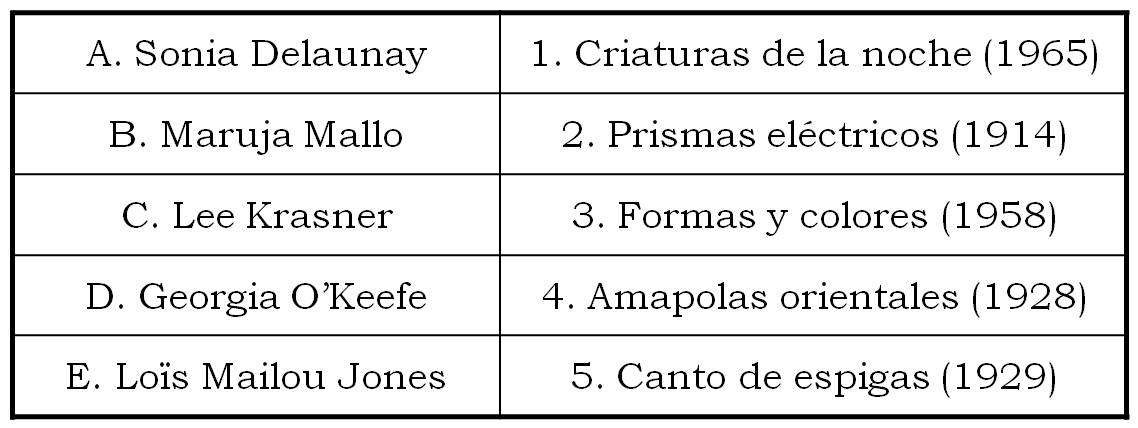
A continuación, podéis ver las obras mencionadas. Y mientras vais viendo cada una de las pinturas podéis intentar asociarla con la artista que la pintó, cuyo nombre es uno de los de la lista de arriba.





Si ya habéis dado una respuesta al juego, podéis seguir adelante con la lectura de esta entrada, aunque si aún no habéis asociado cada artista con una obra podéis volver a mirarlas y haced vuestra elección.
La respuesta correcta a este juego relacionado con el arte es: (A, 2), (B, 5), (C, 1), (D, 4) y (E, 3).
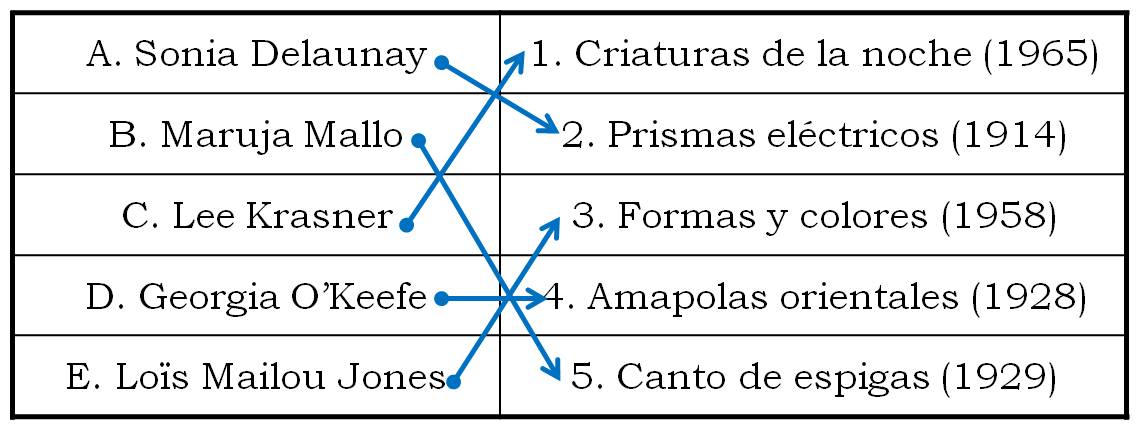
Pero pensemos un poco en el juego y en las diferentes elecciones que se podrían haber hecho. Para empezar, ¿cuántas formas existen de unir los cinco nombres de artistas con los cinco títulos de cuadros, es decir, cuántas posibles respuestas, aunque sean erróneas, tiene el juego?
La solución a esta cuestión seguro que ya la conocéis. Es el número de aplicaciones biyectivas del primer conjunto {A, B, C, D, E} en el segundo {1, 2, 3, 4, 5} o, equivalentemente, de permutaciones de cinco elementos. Si pensamos en que tenemos que asociar a cada una de las letras A, B, C, D y E (que son las artistas), uno de los números 1, 2, 3, 4 y 5 (que son los cuadros), cada posible respuesta al juego es una permutación de los números {1, 2, 3, 4, 5}. Así, la respuesta correcta era la permutación {2, 5, 1, 4, 3}. El número de permutaciones de 5 elementos, o lo que es lo mismo, respuestas al juego de los cuadros, correctas o no, es el factorial de 5, 5! = 5 × 4 × 3 × 2 × 1 = 120. Esto se debe a que, si empezamos por orden, a la artista A la podemos asociar con cada uno de los 5 números {1, 2, 3, 4, 5}, pero una vez realizada una elección para A, y para cada una de ellas, hay 4 posibles elecciones para B. En resumen, para A y B hay en total 5 × 4 = 20 posibles asociaciones de números. Seguimos. Fijadas A y B, y para cada una de las 20 elecciones posibles de ellas, quedarán 3 números libres para poder asociar a C, dos para D, elegida también la opción para C, y finalmente, fijadas las anteriores, solo habrá 1 posibilidad para E. Es decir, las posibles respuestas son 5 × 4 × 3 × 2 × 1 = 120.
Más aún, de esas 5! = 120 posibles respuestas al juego, solo una de ellas es la correcta, como sabemos (A, 2), (B, 5), (C, 1), (D, 4) y (E, 3), pero ¿para cuántas respuestas no habríamos acertado ninguno de los cuadros de las cinco artistas? ¿O un cierto número dado de cuadros, por ejemplo, solo uno? De estas cuestiones vamos a hablar en esta entrada del Cuaderno de Cultura Científica.
Este problema se conoce con el nombre de problema de las cartas extraviadas, o mal dirigidas, aunque también se conoce con otros muchos nombres, entre ellos, el problema de la encargada del guardarropa, el problema de los sombreros, el problema de las coincidencias, el problema de los desarreglos o el problema de Bernoulli-Euler.
El problema dice así:
Determinar el número de permutaciones de n elementos (por ejemplo, los n primeros números {1, 2, …, n}) en las que ningún elemento ocupa su posición natural.
Aunque normalmente el problema se expresa de una forma más divulgativa, cercana al juego que hemos planteado al principio de esta entrada, y que es el motivo por el que recibe el nombre de problema de las cartas extraviadas:
Una persona ha escrito n cartas a n personas distintas (por ejemplo, n amigas suyas) y escribe las direcciones de estas en n sobres. ¿De cuántas formas puede colocar las n cartas en los n sobres de forma que todas las cartas estén en sobres “incorrectos”, es decir, que no lleven la dirección que le corresponde a la carta que contienen?

El problema fue propuesto originalmente por el matemático francés Pierre Rémond de Montmort (1678-1719) en su libro sobre probabilidad y juegos de azar Essay d’analyse sur les jeux de hazard (Análisis de los juegos de azar), de 1708. De Montmort había introducido en su libro un juego de cartas llamado Treize (trece), que es como el juego la ratonera de Arthur Cayley, pero con 4 tacos de 13 cartas (precisamente una baraja francesa de póquer, tiene 52 cartas, con cuatro palos –corazones, diamantes, tréboles y picas– y cada palo con 13 cartas, que podemos considerar numeradas del 1 al 13).

De Montmort se propuso el análisis del juego del Treize, así como algunos problemas más sencillos relacionados con el mismo, entre los que estaba el que denominó el “problema del reencuentro”, que no es otro que el enunciado arriba (problema de las cartas extraviadas).
De Montmort discutió ampliamente este problema con su amigo el matemático Nicolas Bernoulli (1687-1759) en la extensa correspondencia que mantuvieron entre ambos, así como con Johann Bernoulli (1667-1748).
En la segunda edición de su libro Essay d’analyse sur les jeux de hazard, de 1813, de Montmort publica la solución del problema del reencuentro (problema de las cartas extraviadas), así mismo la solución de Nicolas Bernoulli aparece en la correspondencia con de Montmort, la cual es incluida por el francés en esa segunda edición. Otros grandes matemáticos analizaron el problema, como Leonhard Euler (1707-1783) en Calcul de la probabilité dans le jeu de rencontre (1743), Abraham de Moivre (1667-1754) en The Doctrine of Chances (1756), Johann H. Lambert (1728-1777) en Examen d’une espèce de superstition ramenée au calcul des probabilités (1773) o Pierre-Simon Laplace (1749-1827) en Théorie Analytique des Probabilités (1812).

Pero vayamos con la demostración del problema de las cartas extraviadas. La demostración que vamos a mostrar aquí es la realizada por Leonhard Euler, y aparece recogida en el libro 100 Great Problems of Elementary Mathematics: Their History and Solutions.
Vamos a denotar por c1, c2, …, cn los objetos (por ejemplo, las cartas), por S1, S2, …, Sn las posibles posiciones (en la versión de las cartas serían los sobres) y por D(n) el número de permutaciones de n objetos en las cuales ninguno queda en su posición original, es decir, ninguna carta está en el sobre que le corresponde.
Se consideran dos casos:
Caso 1. Las permutaciones de los objetos, esto es, las formas de meter las cartas en los sobres, de manera que la carta c1 está en el sobre S2 (en general, sería cuando el objeto c1 está en la posición S2) y la carta c2 está en el sobre S1.
En este caso, las demás cartas c3, c4, …, cn van a estar en los sobres S3, S4, …, Sn, pero cada una de esas n – 2 cartas ci no está en el sobre correcto Si (i = 3, 4, …, n). Por lo tanto, el número de estas permutaciones es D(n – 2), es decir, el número de permutaciones de n – 2 objetos de forma que ninguno esté en su posición original.
Caso 2. Las permutaciones para las cuales la carta c1 está en el sobre S2, pero la carta c2 no está en el sobre S1.
En estas permutaciones la carta c1 está en el sobre S2, y hay que distribuir las cartas c2, c3, …, cn en los sobres S1, S3, …, Sn, de forma que c2 no esté en S1, c3 no esté en S3, c4 no esté en S4, así hasta la carta cn que no puede estar en Sn. Es decir, si pensamos que al no poder estar la carta c2 en el sobre S1, podemos “asociar” c2 y S1, entonces el número de formas de realizar dicho reparto (la carta c1 está en el sobre S2, pero la carta c2 no está en el sobre S1) es D(n – 1).
En resumen, estos dos casos me muestran que el número de permutaciones de n objetos en las que ningún objeto está en su posición original, pero además c1 está en S2, es igual a
D(n – 2) + D(n – 1).
Y como un argumento similar se puede aplicar a los casos en los que c1 está en S3, S4, …, Sn, se ha demostrado que el número de permutaciones de n objetos en las que ningún objeto está en su posición original es
D(n) = (n – 1) · [D(n – 2) + D(n – 1)]. (fórmula 1)

La fórmula (recursiva) 1 anterior puede reescribirse de la siguiente forma
D(n) – n · D(n – 1) = – [D(n – 1) – (n – 1) · D(n – 2)].
De donde se deduce por recursión y teniendo en cuenta que D(1) = 0 (no hay forma de meter 1 carta en 1 sobre sin acertar), D(2) = 1 (solo hay una forma de meter 2 cartas en 2 sobres de forma incorrecta, cada carta en el sobre que no es) y (–1)n-2 = (–1)n,
D(n) – n · D(n – 1) = (–1)n, (fórmula 2)
puesto que
D(n) – n · D(n – 1) = – [D(n – 1) – (n – 1) · D(n – 2)]
= (–1)2 [D(n – 2) – (n – 2) · D(n – 3)]
= (–1)3 [D(n – 3) – (n – 3) · D(n – 4)]
= … = (–1)n-2 [D(2) – 2 · D(1)].

Si consideramos la fórmula (recursiva) 2 anterior y la dividimos por n!, se obtiene
D(n) / n! –D(n – 1) / (n – 1)! = (–1)n / n!.
De nuevo un argumento recursivo nos lleva a la fórmula
D(n) / n! = (–1)2 / 2! + (–1)3 / 3! + … + (–1)n / n!.
O equivalentemente,
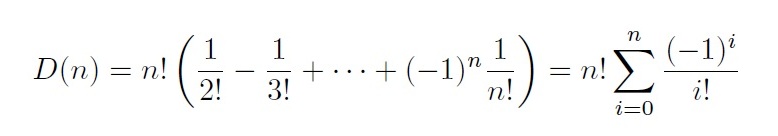
Así, para un número n pequeño de objetos (respectivamente, de cartas) podemos calcular el número D(n) de las permutaciones de esos n objetos en las cuales ninguno queda en su posición original. En concreto, D(3) = 2, D(4) = 9, D(5) = 44, D(6) = 265 y D(7) = 1854. A estos números se les suele conocer con el nombre de números de Montmort o números de desarreglos, y en la Enciclodepia on-line de sucesiones de enteros (OEIS) es la sucesión de números A000166.
Si tenemos en cuenta que en el juego del inicio de esta entrada teníamos cinco artistas, es decir, n es 5, sabemos que el número de soluciones del juego para las cuales no se acierta ni uno solo de los cuadros es D(5) = 44, del total de 120 posibles.
La fórmula obtenida para D(n) se puede demostrar también utilizando el principio de inclusión-exclusión, que es como lo realizó Abraham de Moivre, y quien esté interesado en la misma la puede encontrar por ejemplo en el libro How to count, an introduction to combinatorics.
Pero el problema de las cartas extraviadas, o de los desarreglos, que aquí hemos presentado en su versión combinatoria, suele presentarse también en su versión probabilística.
Problema: Una persona ha escrito n cartas a n personas distintas, escribe las direcciones de estas en n sobres y mete “sin mirar” (al azar) las n cartas en los n sobres. ¿Cuál es la probabilidad de que ninguna de las cartas acabe en el sobre correcto, es decir, con la dirección que le corresponde?
Teniendo en cuenta que la probabilidad de un evento, en este caso que todas las cartas acaben en sobres incorrectos, es igual al número de casos favorables, que es D(n) y acabamos de calcularlo, dividido entre el número de casos posibles, que es n!, entonces dicha probabilidad P(n) es
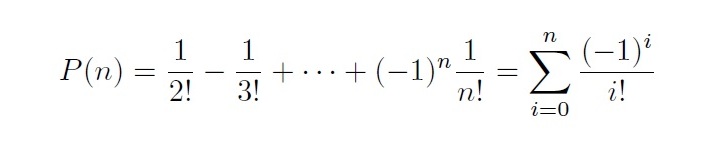
Ahora si tenemos en cuenta la serie de la función exponencial ex:
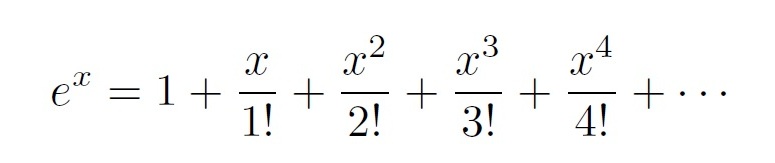
para x = – 1, se tiene que la probabilidad P(n) de que ninguna de las cartas acabe en el sobre correcto se va acercando a 1/e, que es aproximadamente 0,36788 (36,788%), a medida que n va siendo cada vez mayor,
Además, dicha convergencia es muy rápida, como podemos observar en la siguiente tabla.
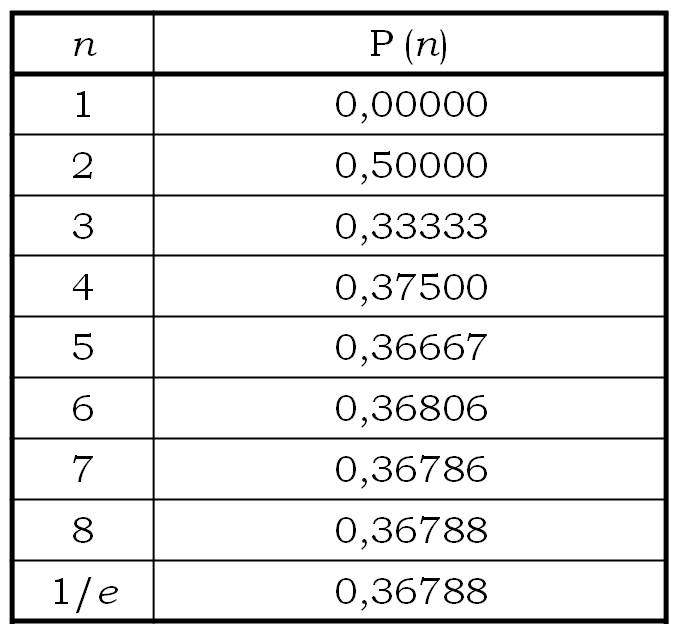
Si volvemos al juego del inicio de esta entrada, observamos que si hemos contestado al azar, la probabilidad de no acertar ni uno solo de los cuadros es del 36,67%, que es bastante alta.
Por otra parte, el problema probabilístico de las cartas extraviadas se puede extender al problema general de que haya un cierto número dado de cartas que sí están en el sobre correcto.
Problema: Una persona ha escrito n cartas a n personas distintas, escribe las direcciones de estas en n sobres y mete “sin mirar” (al azar) las n cartas en los n sobres. ¿Cuál es la probabilidad de que exactamente k de las n cartas acabe en el sobre correcto, es decir, con la dirección que le corresponde?
La respuesta es
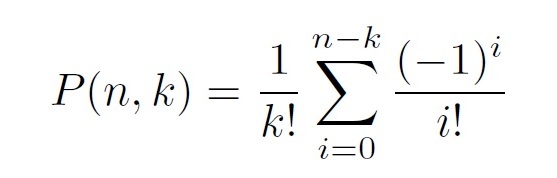
Como curiosidad, si deseamos saber la probabilidad de que solamente una carta de las n posibles acabe en el sobre correcto, observamos que es P(n,1) = P(n – 1). Es decir, para valores grandes de n, esa cantidad se aproxima, de nuevo, a 0,36788 (36,788%).
Vamos a terminar esta entrada del Cuaderno de Cultura Científica recordando un episodio lamentable, el del accidente del Yak-42 en Turquía, en el que el problema de las cartas extraviadas, aunque en esa ocasión se mencionó como el problema de los sombreros, apareció citado en un medio de comunicación.

En el accidente del avión Yak-42 del 26 de mayo de 2006 (para quien desee más información sobre el tema puede consultar aquí ), murieron 62 militares españoles. De los 30 cadáveres que tenían que identificar las autoridades españolas (los otros 32 fueron identificados correctamente por las autoridades turcas), no acertaron ni uno solo, como se menciona en el titular de la siguiente noticia de El País “Defensa no acertó a identificar ni una sola de las víctimas del Yak-42”.
Parecía sorprendente que de las 30 identificaciones, que obviamente habían sido realizadas al azar, no se hubiese acertado ni siquiera una. Como hemos explicado a lo largo de esta entrada, y como se explicó en el recuadro “El problema de los sombreros” de la mencionada noticia de El País, la probabilidad de no acertar en ninguna de las identificaciones (habiendo sido realizadas estas al azar) era del 36,79%, muy alta, luego era bastante probable. Pero si además tenemos en cuenta que, como hemos mencionado también, la probabilidad de que solamente acertaran una identificación también era del 36,79%, entonces la probabilidad de que no acertaran ninguna, o solamente una, identificación era del 73,58%. Muy, muy alta.
Bibliografía
1.- Miodrag S. Petkovic, Famous puzzles of Great Mathematicians, AMS, 2009.
2.- Heinrich Dorrie, 100 Great Problems of Elementary Mathematics: Their History and Solutions, Dover, 1965.
3.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.
4.- Montmort’s Problême du Treize, MacTutor History
of Mathematics archive, 2015.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Don Chogni
Otro ejemplo del mismo problema se encuentra en el lamentable programa de televisión chilena ‘Psíquicos’.
En un episodio, usando sus poderes extrasensoriales los concursantes deben reordenar a 5 matrimonios. No sólo no dan pie en bola; además el que acierta en una pareja (aleatoriamente la probabilidad más alta) es considerado ganador.
https://youtu.be/n5L_rrhnOdc
Pablo
Simplemente corregir el error del límite al infinito, que debe ser de P(n), no de D(n), que son las desordenaciones.
Por lo demás el artículo me encanta, y lo releo en muchas ocasiones.