Cuando asas patatas como guarnición de alguna comida –o como plato principal, porque no– ¿te quedan demasiado crudas, demasiado blandas, demasiado tostadas? Aunque parece algo fácil de hacer, no basta con cortarlas de cualquier manera y meterlas al horno… no, así no siempre quedan bien.

Un grupo de estudiantes de la Edge Hotel School de la Universidad de Sussex (Reino Unido) han recurrido a las matemáticas –que sí, que hasta la cocina necesita de las matemáticas– para solucionar este arduo y capital problema del asado perfecto de las patatas

Basándose en los trucos para conseguir una patata asada perfecta del chef británico Heston Blumenthal, se fijaron en este consejo:

Remember: the more flat edges, the better (Recordad: cuantos más bordes planos, mejor).

A la hora de asar patatas al horno, la peor situación es la de hornear una patata entera, es decir, con mucha curvatura en su superficie, ya que como afirma Blumenthal:

Worst of all is just a round potato, because with a round potato, you haven’t got any corners and edges to get crisp (Lo peor de todo es una simple patata redondeada, porque con una patata curvada, no tienes esquinas ni bordes para lograr una textura crujiente).

Así que, siguiendo los consejos del experto, el objetivo de este grupo de estudiantes era el de calcular la mejor manera de cortar las patatas para conseguir la mayor área plana posible… por supuesto sin desperdiciar la comida. Para hacer este cálculo sin fallos, acudieron a personas expertas en matemáticas en la Samuel Whitbread Academy (Shefford, Reino Unido).

La manera habitual de cortar una patata en cuatro trozos (ver la imagen 1) es dar un corte longitudinal y después otro corte transversal perpendicular al primero.

Sin embargo, cortando en primer lugar la patata en dos piezas longitudinalmente y después en cuatro siguiendo ángulos de aproximadamente 30 grados, las matemáticas dicen que ¡se obtiene la pieza perfecta para asar! Con este corte ‘óptimo’ se gana un 65% de superficie (ver la imagen 2).

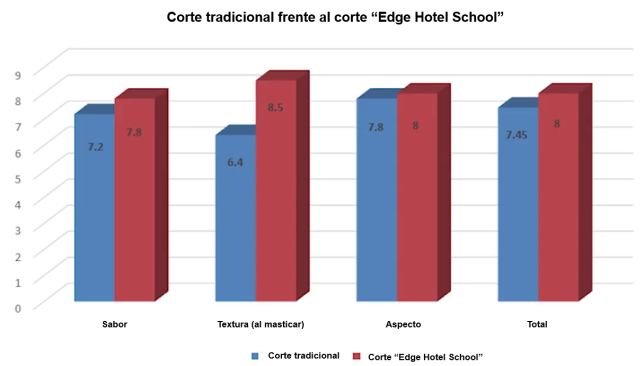
Para experimentar si esta receta avalada por las matemáticas funciona –¿quién puede garantizar que lo ‘óptimo’ sea lo que más gusta? –, los estudiantes probaron su propuesta realizando una cata con la clientela y el personal de cocina de un hotel cercano a su escuela de hostelería. Hicieron probar cien patatas cortadas según sus cálculos –el ‘método Edge Hotel School’– y otras cien cortadas de la ‘manera tradicional’. Teniendo en cuenta tres variables –el sabor, la textura (el crujido al masticar) y el aspecto de las patatas tras el horneado– parece que las patatas cortadas con el método Edge Hotel School gustaron más a los comensales (ver imagen 3)…

Estas patatas asadas ‘de manera perfecta’ pueden acompañarse, por ejemplo, de pollo frito. Pero, cuidado, para repartir equitativamente la carne entre los comensales de nuevo necesitarás de las imprescindibles matemáticas. Debes estudiar sin falta el teorema del pollo picante. Y por supuesto, bon appétit…

Referencias:

Phoebe Weston, Science behind the perfect roast potato: Slice the spud at 30-degree angles to increase its surface area and make it extra crispy, say researchers, Daily Mail, 16 enero 2018

Declan Cashin, How maths can give you the perfect roast potato, BBC, 25 enero 2018

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.