El tamaño de los animales es una variable que ha de ser tenida en cuenta siempre que estudiemos su funcionamiento. La razón de su importancia es que un buen número de funciones cursan a velocidades que dependen del tamaño, pero esa dependencia no corresponde a una proporcionalidad lineal estricta. El caso mejor conocido y de más profundas implicaciones es el de la tasa metabólica, que expresa la velocidad a la que transcurre el conjunto de reacciones químicas que configuran el metabolismo de un organismo.

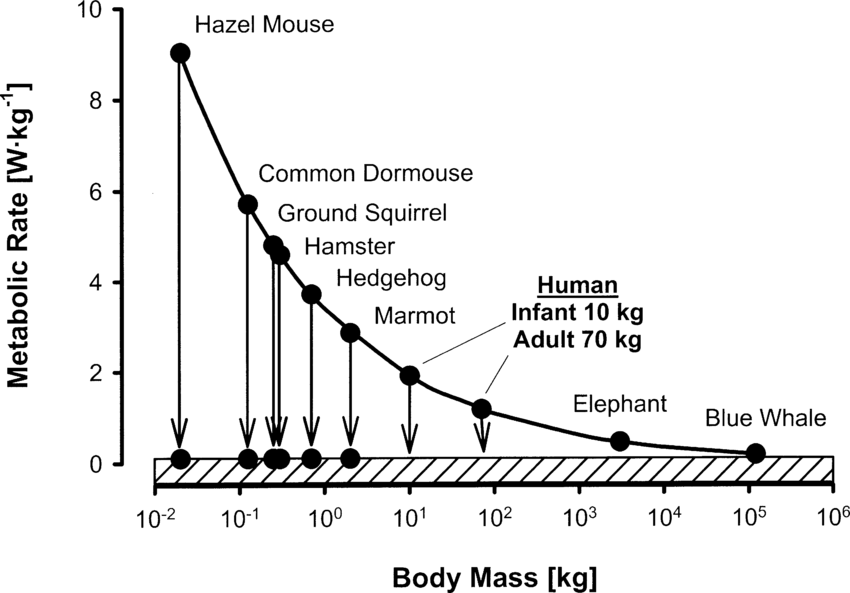
La tasa metabólica de un animal en reposo depende de su masa de acuerdo con la función potencial M = a W^b. En tal ecuación el coeficiente a puede tomar valores diversos dependiendo de las condiciones ambientales en que se encuentra el animal y de otras circunstancias, y la potencia b toma valores que pueden diferir entre especies y condiciones ambientales, pero que, para el conjunto de animales, es de 0,75. Por lo tanto, la tasa metabólica específica de masa (M/W) puede expresarse de acuerdo con la ecuación M/W = a W^b W^-1 = a W^b-1 y, por lo tanto M/W = a W^-0.25. O sea, la tasa metabólica es mayor cuanto menor es el tamaño de los animales.

Todas las actividades animales conllevan gasto de energía, por lo que requieren su suministro en forma de ATP o moléculas equivalentes. Y en la inmensa mayoría de los casos ese suministro se produce gracias al catabolismo de sustratos energéticos que utiliza el O₂ como aceptor final de electrones en la cadena respiratoria mitocondrial. Por ello, el consumo de oxígeno (VO₂) constituye el indicador universal del nivel que alcanza el conjunto de actividades que constituyen el metabolismo.

Dado que, como se ha señalado, la actividad metabólica varía en función de la masa de los animales de acuerdo con una función potencial en la que b vale 0.75, interesa indagar acerca de la dependencia existente entre las variables implicadas en la captación de oxígeno del exterior y el tamaño. Y para ello, debemos expresar el consumo de oxígeno en función de los parámetros respiratorios relevantes. Así, VO₂ = V_a (C_i –C_e), siendo V_a la tasa ventilatoria -que es el volumen de medio respiratorio que intercambia el órgano respiratorio con el exterior por unidad de tiempo-, y (C_i – C_e), la diferencia de concentración de oxígeno entre las corrientes inhalante y exhalante.

La diferencia entre las concentraciones inhalante y exhalante de oxígeno es, para la generalidad de los animales, independiente del tamaño. En términos matemáticos la potencia que relaciona la diferencia entre esas concentraciones y la masa de los animales es igual a 0; o sea, (C_i – C_e) = a’ W⁰. La tasa ventilatoria, sin embargo, sí varía con el tamaño, y lo hace de acuerdo con una dependencia similar a la del metabolismo. Aunque el valor de b puede variar entre especies, si se consideran en conjunto las aves y los mamíferos (que son los grupos para los que se dispone de mayor volumen y mejor información), ese valor no difiere significativamente de 0.75. Así pues, V_a = a’’ W^0.75, como cabía esperar, puesto que si VO₂ = a W^0.75y (C_i – C_e) = a’ W⁰, y dado que V_a = VO₂/(C_i – C_e), entonces V_a = a/a’ W^{0.75 – 0}; o sea, V_a = a’’ W^0.75. En definitiva, cuanto mayor es el tamaño de un animal mayor es su tasa ventilatoria, pero esta última crece más lentamente cuanto más crece aquel o, lo que es lo mismo, la diferencia entre dos animales de distinto tamaño no es de la misma magnitud relativa que la diferencia entre los tamaños, sino que la tasa ventilatoria aumenta en menor medida que lo hace la masa del animal.

Por otro lado, la tasa ventilatoria es, a su vez, el producto entre la frecuencia respiratoria o número de ciclos respiratorios por unidad de tiempo (f_c) y el volumen corriente (en inglés tidal volume) (VC): V_a = f_c VC. El volumen pulmonar y el volumen traqueal de aves y mamíferos son linealmente proporcionales a la masa del animal. Parece lógico, por ello, que el volumen corriente exhiba el mismo tipo de dependencia con el tamaño. En efecto, VC = a’’’ W¹. Eso sí, la frecuencia respiratoria disminuye cuanto mayor es un animal de acuerdo con una función en la que la potencia que afecta a la masa vale -0.25; o sea: fc = a’’’’ W^-0.25. Así ha de ser, dado que V_a = a’’ W^0.75 y VC = a’’’ W¹, por lo que f_r = a’’ W^0.75/ a’’’ W¹= a’’/a’’’ W^0.75-1 = a’’’’ W^-0.25. En definitiva, cuanto mayor es un animal, menor es la frecuencia de sus ciclos respiratorios, o lo que es lo mismo, respira más lentamente.

Fuentes:

William A. Calder III (1996): Size, Function and Life History. Dover Publications Inc, Mineola, NY, EEUU.

Knut Schmidt-Nielsen (1984): Scaling: Why Animal Size is so Important. Cambridge University Press, Cambridge, RU

Geoffrey W. West (2017): Scale. Penguin Random House, NY, EEUU

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU