En la entrega anterior vimos cómo la definición del trabajo en la física era mucho más comprensible y de “sentido común” de lo que suele apreciarse.

Hasta aquí estupendo, pero, ¿qué tiene que ver esto con la energía y los mecanismos?

La primera ley de la termodinámica nos dice que la variación de energía (ΔU) de un sistema se produce por el intercambio de calor (Q) y de trabajo (W).

ΔU = Q + W

No nos meteremos aquí con el asunto del calor, estamos pensando en mecanismos que cambian tipos de movimiento y su velocidad, entenderemos que habrá pérdidas por rozamiento, pero consideraremos el caso ideal sin pérdidas (recordad que soy físico).

Así que elijamos un mecanismo, una palanca, por ejemplo.

No hay más aportes de energía que la que hacemos en un extremo mediante nuestra fuerza y eso es todo lo que tendremos a la salida. La energía que entra será la que salga, y ambas serán trabajo (ya, ya, salvo pérdidas).

Así que podemos decir que

W₁ = W₂

Como hemos visto, nuestro trabajo tiene dos factores, la fuerza y la distancia (supongamos alineación entre ellos). Por lo que podríamos conseguir 10 J (unidades de trabajo) de muchas maneras, por ejemplo:

W = F · d

1 · 10 = 10 J

2 · 5 = 10 J

5 · 2 = 10 J

10 · 1 = 10 J

…

Mandaremos la misma energía (trabajo) de un extremo al otro del mecanismo, pero podemos hacerlo con más fuerza y menos recorrido o al revés, según nos interese.

¿Podría ser entonces que en un extremo del mecanismo tuviéramos más fuerza que en el otro? Por supuesto, no existe nada parecido a un “principio de conservación de la fuerza”. Tú puedes multiplicar tu fuerza lo que desees (idealmente, claro). De ahí viene la expresión “Dadme un punto de apoyo y moveré el mundo”.

Supongo que ya te habrás dado cuenta de que ese aumento de fuerza tiene un precio. Tendrás que reducir el recorrido en la misma proporción, de forma que la energía se mantenga constante, porque para la energía sí tenemos una ley de conservación.

Así que, sin más, podemos afirmar que si en un mecanismo el recorrido que se hace a la salida es la mitad que el que se hace a la entrada, la fuerza será el doble. No necesitamos saber nada más de lo que ocurre en el interior del mecanismo. Estoy haciendo balance de energía a la entrada y a la salida, punto. Pura conservación de la energía que no se la salta nadie, primera ley de la termodinámica.

Volvamos a nuestra palanca, mediante argumentos geométricos podemos saber qué relación hay entre las distancias recorridas a un lado y a otro, y eso nos llevará, vía conservación de la energía, a concluir la relación entre las fuerzas a ambos extremos. Vaya, llegaremos a la “ley de la palanca”.

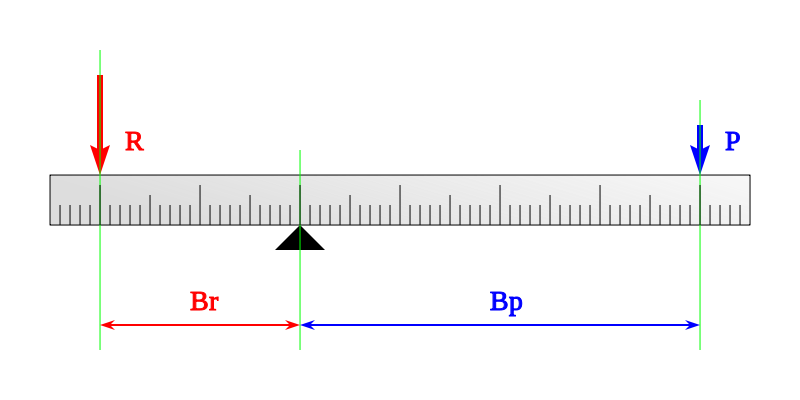
La Palanca

Vemos que los extremos de la palanca recorren ambos un arco de circunferencia, cuyos radios son Br y Bp, y son obviamente distintos en longitud, así que ya estamos en condiciones de afirmar que las fuerzas a ambos lados también lo serán.

Fíjate que los ángulos recorridos en ambos extremos son iguales, en caso contrario la barra se doblaría.

Pero a nosotros nos interesa la distancia (para la fórmula del trabajo), así que pensemos en la longitud del arco de circunferencia que se recorre.

Esa longitud de arco es proporcional al radio y al ángulo. Si recordáis la popular fórmula para la longitud de la circunferencia completa L = (2π)·r es justo esa proporcionalidad para un ángulo de 2π radianes, lo que en grados sería 360º.

Por lo tanto, para un arco cualquiera sería:

arco = ángulo · radio de giro

Sigamos adelante, comparemos trabajos:

W1 = W2

W = F·d (suponiendo fuerzas alineadas con el desplazamiento)

R · arco1= P · arco2

R · ángulo · Br = P · ángulo · Bp (ya que los radios de giro son Br y Bp)

Como los ángulos son iguales, si la barra no se dobla, podemos simplificar

R · Br = P · Bp

¡Hecho! Fuerza por su brazo igual a fuerza por su brazo. La ley de la palanca.

Vemos que simplemente hemos aplicado argumentos geométricos para averiguar la distancia recorrida al principio y al final del mecanismo y después la conservación de la energía para ver la relación entre las fuerzas.

En la próxima entrega haremos los cálculos para varios mecanismos, pero os animamos a que lo probéis vosotros y, si sois docentes, que se lo pongáis a vuestros (pobres) alumnos como ejercicio.

Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de escritor de libros de divulgación.