En la entrada Clasificando en topología: de lo local a lo global recordábamos un bellísimo teorema de clasificación:

Dada una superficie compacta (cerrada y acotada) y conexa (de una pieza), es topológicamente equivalente a una esfera, a una suma conexa de toros o a una suma conexa de planos proyectivos.

Una vez demostrado este teorema, surge una pregunta natural: ¿son estos tipos de superficies topológicamente diferentes? Es decir, ¿podría suceder que, para dos enteros positivos distintos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m toros? ¿Y podría ocurrir que, para dos enteros positivos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m planos proyectivos?

Para demostrar que esto no es posible se puede recurrir a un invariante numérico llamado la característica de Euler que tiene sus raíces en la conocida fórmula de Euler para poliedros que afirma que

Si P es un poliedro convexo con f caras, e aristas y v vértices, entonces v–e+f=2.

La fórmula de Euler para poliedros se puede generalizar a superficies compactas. Antes de comentar cómo, recordemos que cualquier superficie compacta y conexa puede obtenerse como el cociente de una región poligonal en el plano con un número par de aristas identificadas a pares. Cada superficie puede reconocerse a través de una presentación quese obtiene etiquetando con el mismo símbolo cada par de aristas identificadas y “leyendo” estas etiquetas en el orden en el que se presentan.

Por ejemplo, la esfera, el plano proyectivo, el toro y la botella de Klein son cocientes de cuadrados como se indica en la imagen de debajo. Cada flecha y cada letra indican las aristas que se identifican y la forma de realizar este “pegado”.

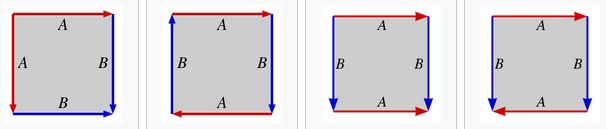
Cada una de las anteriores superficies tendría las presentaciones (empezando a “leer” desde la esquina superior izquierda):

1. la esfera: ABB^-1A^-1,

2. el plano proyectivo real: ABAB,

3. el toro: ABA^-1B^-1, y

4. la botella de Klein: ABAB^-1

Una superficie no tiene una única presentación, depende de la manera de etiquetar. Pero dos presentaciones de la misma superficie son equivalentes en el sentido de que pueden transformarse la una en la otra por una serie de operaciones elementales. Los detalles pueden verse en [1], en las páginas 8 a 16.

Si S es una superficie con una presentación P dada, se define la característica de Euler de esa presentación como χ(P) = v–e+f, donde f es el número de caras, e el dearistasy v el de vértices de la presentación. Por ejemplo,

1. La esfera, con la presentación P=ABB^-1A^-1, tiene χ(P)=2–1+1=2 (tras las identificaciones, contamos 2 vértices, 1 arista y 1 cara).

2. El plano proyectivo real, con la presentación P=ABAB, tiene χ(P)=2–2+1=1 (tras las identificaciones, contamos 2 vértices, 2 aristas y 1 cara).

3. El toro, con la presentación P=ABA^-1B^-1, tiene χ(P)=1–2+1=0 (tras las identificaciones, contamos 1 vértice, 2 aristas y 1 cara).

4. La botella de Klein, con la presentación P=ABAB^-1, tiene χ(P)=1–2+1=0 (tras las identificaciones, contamos 1 vértice, 2 aristas y 1 cara).

Se puede probar que χ(P) es un invariante de la superficie, es decir, no depende de la presentación dada para S; por ello se denota por χ(S) y se llama característica de Euler de la superficie. Además se demuestra que si S es homeomorfa a una esfera, entonces χ(S)=2, si es homeomorfa a la suma conexa de n toros es χ(S)=2−2n, y si es homeomorfa a la suma conexa de n planos proyectivos es χ(S)=2−n.

Con esto queda respondida la primera pregunta planteada al principio, ¿podría suceder que, para dos enteros positivos distintos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m toros? No, porque poseen distintas características de Euler.

¡Vaya! Pero la suma conexa de 2n planos proyectivos tiene la misma característica de Euler que la suma conexa de n toros. ¿Son ambas superficies homeomorfas? No, pueden distinguirse porque la primera superficie (suma conexa de 2n planos proyectivos) no es orientable, mientras que la segunda (suma conexa de n toros) si lo es. Y la orientabilidad es una propiedad topológica. Así que, para dos enteros positivos m y n, la suma conexa de n toros no puede ser homeomorfa a la suma conexa de m planos proyectivos…

Es decir, queda demostrado el siguiente teorema:

Si S₁ y S₂ son superficies compactas y conexas, son homeomorfas si y sólo si son ambas orientables o ambas no orientables y χ(S₁)=χ(S₂).

El anterior es un teorema topológico por excelencia. Se ha reducido el problema de clasificación de superficies compactas a la determinación de dos invariantes topológicos: la orientabilidad y la característica de Euler, ambos fácilmente calculables.

Nota 1: Los poliedros aludidos en la fórmula de Euler son homeomorfos a una esfera. Por eso su característica de Euler es 2.

Nota 2: El matemático Simon Antoine Jean L’Huillier (1750-1840) nació un 24 de abril. Generalizó la fórmula de Euler a poliedros con g asas: v–e+f=2-2g.

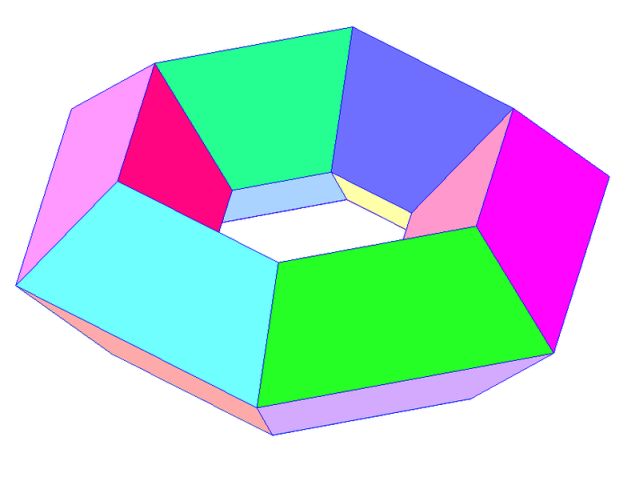
Existe una relación entre la característica de Euler χ(S) de una superficie S y g(S), su número de asas. Si S es orientable, g(S)=1/2(2-χ(S)). Y si no lo es, entonces g(S)=2-χ(S). ¿Y qué son las asas de una superficie? Una esfera no posee asas, y la suma conexa de n toros o de n planos proyectivos posee n asas…

Referencia

[1] Marta Macho Stadler, Topología Algebraica, Apuntes Máster 2014-2015

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.