A menudo, las innovaciones en ciencia son, ante todo, herramientas que simplifican la manera de abordar un problema, transformaciones que lo hacen más aprehensible a través de nuestros sentidos (la vía que tenemos para incorporar nueva información a nuestros modelos mentales, al fin y al cabo). Pensemos, por ejemplo, en la importancia de la notación en matemáticas. Representar una derivada con un símbolo o con otro puede parecer una discusión vacía, una cuestión de forma al fin y al cabo. Pero es que la forma (en ciencia, así como en arte) posibilita la aparición de nuevos contenidos. Si no, como propone Pablo Rodríguez, probad a hacer multiplicaciones con lápiz y papel usando números romanos.

Del mismo modo, si John Snow hubiese intentado hacer su análisis de la epidemia del cólera usando sólo datos (víctimas y coordenadas, números desnudos), probablemente le hubiese costado mucho más llegar a la misma conclusión. O quizás nunca la hubiese alcanzado. Las gráficas se han convertido así en un recurso fundamental de la ciencia. Y, sin embargo, no siempre parecen recibir un servicio recíproco. En muchos casos, pensamos en este tipo de herramientas como una cuestión de “gusto” o de “intuición”: todo elemento gráfico puede configurarse según le dé al perpetrador (para eso se inventó la galería de horrores del Excel).

Nada más lejos de la realidad. No cualquier cosa vale, ni todos los recursos visuales son igualmente adecuados. Como en todo fenómeno observable, la efectividad de una gráfica también puede ser medida y comparada. Es posible hacer ciencia de las gráficas de datos, y esto fue lo que se propusieron William S. Cleveland y Robert McGill en los años 80¹:

Hoy en día, los gráficos son una parte vital del análisis de datos estadísticos y una parte vital de comunicación en ciencia y tecnología, negocios, educación y los medios de masas. Y aun así, el diseño de gráficos para el análisis y presentación de datos se hace en gran medida sin rigor científico.

Así, decidieron desarrollar y testar empíricamente unos principios básicos de la percepción gráfica. Para ello, formaron un modelo basado en tareas perceptivas elementales que realizamos cuando decodificamos información cuantitativa en gráficas, y las pusieron a prueba a través de experimentos.

El resultado es una teoría que permite predecir el rendimiento relativo de diferentes gráficas basándose en los elementos que la componen. De hecho, concluían que era necesario reemplazar muchos de los tipos de gráficas populares en aquel entonces (y que, desgraciadamente, todavía lo son; por ejemplo, la tristemente común gráfica de tarta).

Los elementos perceptivos que identifica la teoría de Cleveland y McGill, ordenados de mayor a menor exactitud perceptiva, son los siguientes:

1. Posición en una escala común.
2. Posición en escalas no alineadas.
3. Longitud, dirección, ángulo.
4. Área.
5. Volumen, curvatura.
6. Sombreado, saturación de color.

En otras palabras, las tareas que involucran elementos más simples —como los puntos, las líneas o las barras— son las que mejor funcionan perceptivamente, lo cual no resultará una sorpresa. Así, los diagramas de dispersión, las gráficas de evolución, de distribución y de comparación de magnitudes son las más efectivas para codificar un mensaje complejo. A medida que los recursos gráficos se van haciendo más complejos, aumentan las dificultades de lectura. La situación se vuelve dramática cuando se introducen elementos en 3D, que involucran profundidad y volumen. Porque, aunque somos relativamente buenos con la perspectiva, no olvidemos que las gráficas son generalmente imágenes planas, en 2D, donde la diversidad espacial que nos proporciona el hecho de tener dos ojos resulta totalmente inútil.

Estudios posteriores han refinado esta escala, añadiendo otros parámetros como tono de color y profundidad de campo. La escala, finalmente, queda como podéis ver aquí:

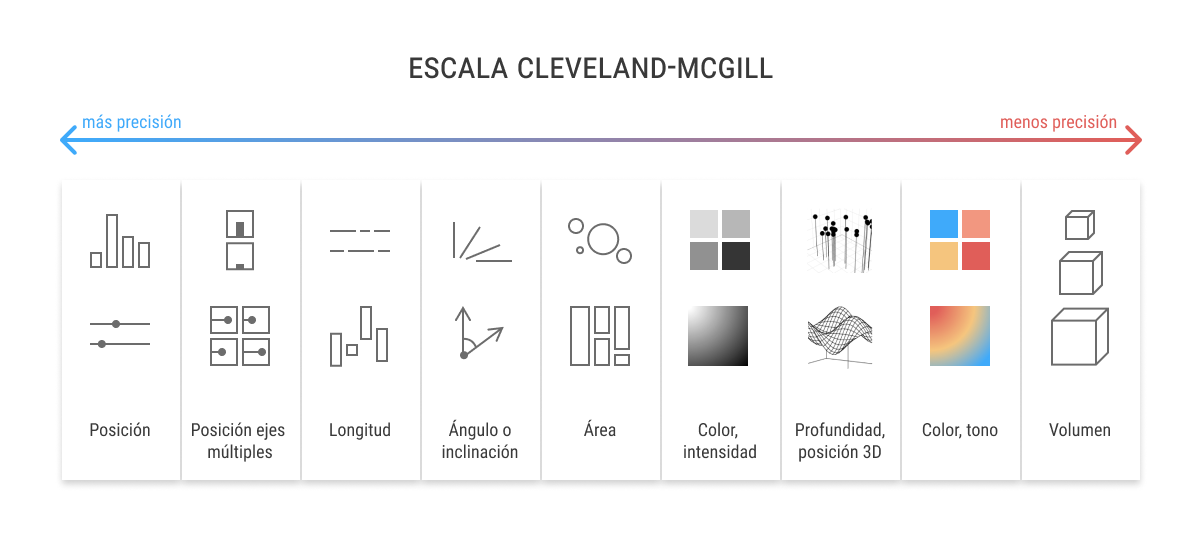
Como los propios autores originales admitían, obviamente estas tareas no son lo único que influye en la construcción de una buena gráfica, ni el único tipo de tareas que llevamos a cabo cuando leemos este tipo de representación visual. Pero sirve como base para priorizar unas tareas sobre otras y seleccionar el atributo más efectivo dependiendo de los datos que se vayan a representar.

Referencia: