El pasado mes de mayo, aprovechando la exposición de la artista Esther Ferrer en Tabakalera (Donostia), Esther Ferrer, 2, 3, 5, 7, 11, 13, 17, 19, 23…, dedicamos dos entradas del Cuaderno de Cultura Científica a su serie de obras Poema de los números primos, en la cual utiliza los números primos como herramienta en el proceso de creación artística:

i) Poema de los números primos

ii) Poema de los números primos (2)

En la entrada de hoy vamos a hablar de otro artista que también ha utilizado los números primos en la creación de una de sus obras de arte, es el artista británico Anthony Hill.

Anthony Hill nació en Londres en 1930, formó parte del movimiento artístico de los constructivistas británicos y estuvo relacionado con el Grupo Sistemas. Heredero del arte concreto, Anthony Hill utiliza las matemáticas en el proceso creativo artístico. Tiene un profundo conocimiento de esta ciencia, publicando incluso algunos artículos de investigación matemática, como el artículo On the number of crossings in a complete graph (Proceedings of the Edinburgh Mathematical Society 13, n. 4, p. 333-338, 1963), junto al matemático Frank Harary, o siendo elegido Honorary Research Fellow en el Departamento de Matemáticas del University College de Londres.

La obra que vamos a analizar en esta entrada es Prime Rhythms / Ritmos primos (1959 -1962).

Esta obra está inspirada en los números primos y, más concretamente, en los números primos gemelos. Recordemos que los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 30 no es un número primo ya que se puede dividir por 2, 3, 5, 6, 10 y 15, además de por 1 y 30, o tampoco el 33, divisible por 3 y 11, mientras que el número 13 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que los números 2, 3, 5, 7, 11, 17 o 19. Por motivos formales el número 1 es considerado no primo en matemáticas, aunque en esta obra Anthony Hill lo va a incluir el en grupo de los números primos.

Lo primero que hace el artista británico es considerar todos los números impares menores que 100 (tengamos en cuenta que los números pares, con la excepción del 2, son siempre compuestos, es decir, no primos) y dividir este grupo en dos subgrupos, los primos y los compuestos. Resulta que hay exactamente la misma cantidad de elementos en cada subgrupo, en concreto, veinticinco.

Números primos impares menores que 100:

1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Números compuestos impares menores que 100:

9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95.

A continuación, Anthony Hill toma un cuadrado, considera la línea intermedia y marca 50 líneas horizontales, igualmente espaciadas, de forma que cada una de ellas es un número impar menor que 100, desde el 1 hasta el 99. Aunque cada línea es un número impar, los números impares primos los considera a la izquierda y los números impares no primos a la derecha, como se muestra en la siguiente imagen esquemática de los primeros números.

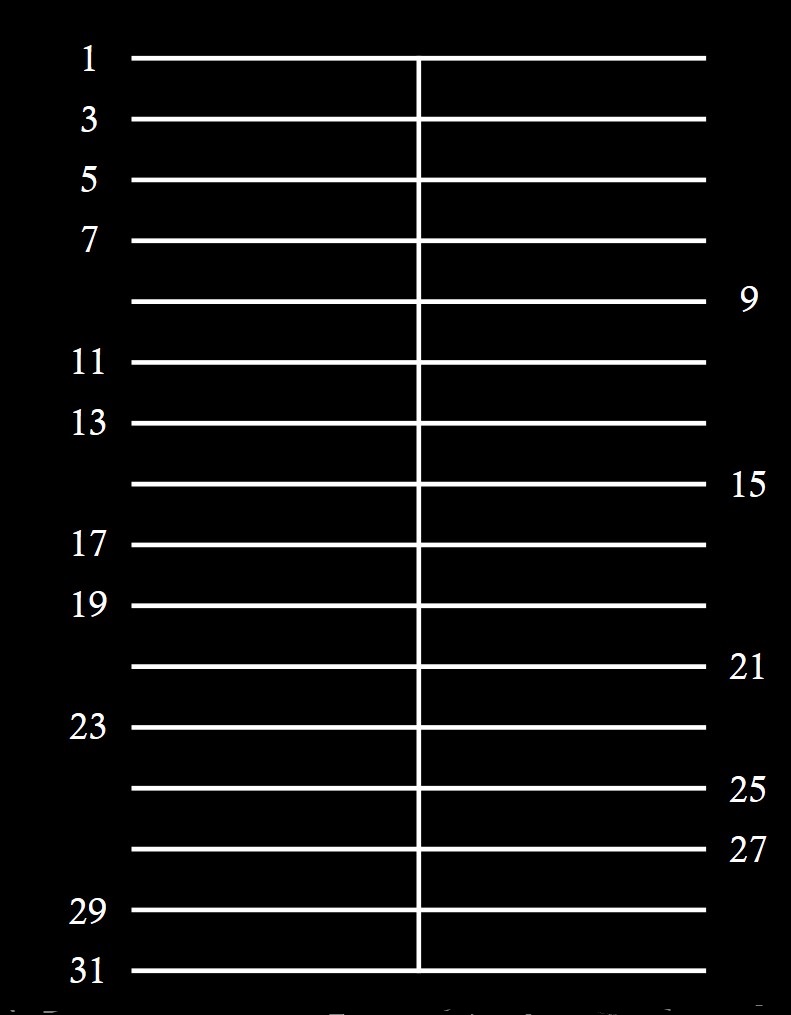
El siguiente paso fue considerar los números primos gemelos, que son aquellos números primos que están lo más cerca posible (con la excepción del 2 y el 3), es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, 41 y 43, 59 y 61, 71 y 73. Anthony Hill considera los números primos (impares) gemelos, que además son menores de 100, como se ve en la siguiente imagen, en la parte de la izquierda. Observemos que, al considerar solo números impares, los números primos gemelos son números consecutivos, 1 y 3, 3 y 5, 5 y 7, 11 y 13, 17 y 19, y 29 y 31, en la siguiente imagen.

Por otra parte, Anthony Hill considera los números no primos impares consecutivos, que podríamos denominar ahora “números compuestos impares gemelos”. Como por ejemplo el par 25 y 27, que se puede ver en la parte de la derecha de la imagen, aunque hay más, como 33 y 35.

La siguiente acción es pintar de negro las zonas, o bandas entre líneas paralelas, que se corresponden a números gemelos, para los números primos, a la izquierda, y para los números impares no primos, a la derecha, y las demás bandas de color blanco. Podemos apreciar la construcción en la siguiente imagen.

Por lo tanto, sin marcar la separación entre las zonas que hemos realizado en el anterior esquema explicativo, podemos realizar la siguiente recreación de la obra Prime Rhythms / Ritmos primos de Anthony Hill.

Terminamos la entrada mostrando una obra de Anthony Hill relacionada con los grafos, The Nine – Hommage à Khlebnikov / El nueve, homenaje a Khlebnikov (1976).

Bibliografía

1.- Anthony Hill, A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief, Leonardo, Vol. 10, No. 1, pp. 7-12, 1977.

2.- Alan Fowler, A Rational Aesthetic. The Systems group and associated artists, Southampton City Art Gallery, 2008.

3.- Michael Holt, Mathematics in Art, Littlehampton Book Services, 1971.

4.- Raúl Ibáñez, Las Matemáticas como herramienta en la creación artística (conferencia), Curso de verano de la UPV/EHU, “Cultura con M de matemáticas, una visión matemática del arte y la cultura”, 2019.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica