El puzle Stomachion y el palimpsesto de Arquímedes (1)
En esta mini-serie de dos entradas del Cuaderno de Cultura Científica me gustaría hablar del puzle geométrico de tipo Tangram más antiguo que se conoce, el Stomachion. Pero antes de hablar de este puzle geométrico, me parece interesante que empecemos esta historia por el palimpsesto de Arquímedes, que incluye la copia más extensa de la obra original Stomachion del matemático griego.
Según el diccionario de la RAE, “palimpsesto” es un “manuscrito antiguo que conserva huellas de una escritura anterior borrada artificialmente”. Además, este término viene del latín palimpsestus, que a su vez deriva del griego παλίμψηστος palímpsēstos, que significa “grabado nuevamente”.
En la antigüedad, desde antes del tercer milenio a.n.e., los manuscritos, pensemos en todo tipo de textos, literarios, científicos, religiosos, filosóficos, políticos, etc, eran escritos en papiro, que era un soporte realizado a partir de una planta acuática, Cyperus papyrus, muy común en el río Nilo (en Egipto) y en algunos otros lugares del mediterráneo. Su elaboración era muy delicada y además era un material que se deterioraba muy pronto, por lo cual poco a poco empezó a dejar de usarse (hacia el siglo V, desapareciendo completamente en el siglo XI) y se emplearon otros materiales, como el pergamino.

El término pergamino viene de la ciudad de Pérgamo, en la actual Turquía, que era una gran ciudad editorial, rival de la Biblioteca de Alejandría en Egipto, motivo por el cual Alejandría prohibió la exportación de papiro, dejando sin material de trabajo a los bibliotecarios de Pérgamo, que tuvieron que utilizar el pergamino. Este es una piel de un animal, por ejemplo, res, oveja o cabra, limpia de pelo, adobada y estirada, que fue utilizada para escribir sobre ella o cubrir libros.
A partir del siglo VI, debido tanto a los problemas con el papiro, como a la escasez y alto coste del pergamino, empezaron a reutilizarse los pergaminos para escribir nuevos textos. Además, tenemos que recordar que el papel, inventado en China hacia el siglo II a.n.e., aún tardaría mucho tiempo en establecerse en Europa. Para reutilizar el pergamino, primero había que “borrar” el texto original, ya fuese mediante el raspado de la tinta con algún material, como la piedra pómez, o utilizando alguna sustancia ácida, como el jugo de naranja, que borrase el texto.
De esta forma desaparecieron las obras recogidas en muchos de estos manuscritos antiguos, aunque a diferencia de las obras que se perdieron por la destrucción de miles de papiros de la antigua Biblioteca de Alejandría en las diferentes catástrofes que la asolaron, el tratamiento moderno de los palimpsestos encontrados ha permitido rescatar el contenido antiguo de los mismos y, en muchas ocasiones, recuperar obras que se creían perdidas para siempre. Uno de los ejemplos es el conocido Palimpsesto de Arquímedes.

Arquímedes (aprox. 287 – 212 a.n.e.) fue sin lugar a dudas uno de los sabios más importantes de la Antigua Grecia. Junto con Euclides (aprox. 325 – 265 a.n.e.) y Pitágoras (aprox. 585 – 500 a.n.e.) forman la terna de matemáticos griegos más importantes de la Antigüedad. Mientras que podemos considerar a Pitágoras como el gran matemático puro, teórico, y Euclides el gran maestro, e incluso, divulgador, por su gran obra Los Elementos, que contiene el saber matemático de la época, el sabio de Siracusa, Arquímedes, puede ser considerado el gran matemático aplicado, de hecho, se le suele citar como el primer ingeniero.
El conocido como Palimpsesto de Arquímedes era originalmente un manuscrito escrito en griego en el siglo X con algunas obras del matemático a quien se atribuye la frase “dadme un punto de apoyo y levantaré el mundo”. El manuscrito consistía en una copia de una recopilación de alrededor del año 530 de las obras de Arquímedes realizada en Constantinopla por el arquitecto griego bizantino Isidoro de Mileto, quien diseñó junto a Antemio de Trales la Iglesia de Santa Sofía de Constantinopla (en la actualidad, Estambul).
En 1229 un monje cristiano, Johanes Myronas, separó los folios del manuscrito con las obras de Arquímedes, los raspó y lavó, para eliminar el texto original, los dobló por la mitad y los tomó en perpendicular al sentido original. Entonces los juntó a los pergaminos borrados de otras obras, como algunos discursos del político ateniense Hipérides (siglo IV a.n.e.), con el objetivo de convertirlo en un texto litúrgico de 177 páginas numeradas, de las cuales se conservan 174.
Las obras de Arquímedes contenidas en el palimpsesto son:
1) Sobre el equilibrio de los planos;
2) Sobre las espirales;
3) Medida de un círculo;
4) Sobre la esfera y el cilindro;
5) Sobre los cuerpos flotantes, que es la única copia en griego que se ha conservado, que se sepa, de esta obra;
6) El método de los teoremas mecánicos, que es la única copia que existe de esta obra y que se ha podido recuperar gracias al descubrimiento del palimpesto; y
7) la copia más completa que existe de la obra Stomachion, sobre este puzle geométrico de tipo Tangram.

El Palimpsesto de Arquímedes estuvo en el monasterio ortodoxo griego Mar Saba, a las afueras de Belén, en Cisjordania, al menos hasta el siglo XVI, pero en algún momento antes de 1840 fue a parar a la biblioteca de la Iglesia Ortodoxa de Jerusalén, el metoquión del Sagrado Sepulcro, en Constantinopla. Allí lo encontró el teólogo y estudioso de la Biblia alemán, Constantin von Tischendorf (1815 – 1874), quien intrigado por la matemática que aún quedaba visible en algunas partes del palimpsesto, se llevó uno de sus folios, aunque no fue consciente de la importancia de lo que tenía delante. Ese folio se vendería tras su muerte a la Universidad de Cambridge, pero no se identificó como uno de los folios del Palimpsesto de Arquímedes hasta 1968.
El erudito griego Papadopoulos-Kerameus catalogó, en 1899, los manuscritos de la biblioteca y tradujo algunas de las líneas del texto griego original. Cuando el filólogo e historiador danés Johan L. Heiberg (1854 – 1928), experto en matemática griega y que ya unos años antes había realizado una edición de las obras completas de Arquímedes, leyó esas líneas, se dio cuenta de que eran del matemático de Siracusa, más concretamente de su obra Sobre la esfera y el cilindro. Entonces, viajó a Constantinopla, en 1906, para estudiarlo y descubrió que contenía las siete mencionadas obras matemáticas. Todo un descubrimiento. Heiberg fotografió el manuscrito (es decir, su análisis del palimpsesto fue mediante visión directa, de lo que se podía ver y leer a simple vista), estudió su contenido y lo incluyó en su edición de las obras completas de Arquímedes de 1910 y 1915.



Johan Heiberg viajó por última vez al metoquión del Sagrado Sepulcro en 1908, momento en el que la historia se vuelve un poco oscura hasta que en octubre 1998 la casa de subastas Christie’s de Nueva York sacó a subasta el Palimpsesto de Arquímedes, anunciado como perteneciente a una colección privada francesa. El 28 de octubre, un día antes de la anunciada subasta, el Patriarcado de la Iglesia Ortodoxa de Jerusalén llevó a Christie’s ante la Corte Federal de Nueva York para que detuvieran la venta del manuscrito y fuese reconocido como su propietario legal. Sin embargo, la Corte Federal de Nueva York no le dio la razón y el palimpsesto fue vendido por dos millones de dólares a un coleccionista privado del mundo de la tecnología. En un principio se pensó que el comprador anónimo era Bill Gates, cofundador de Microsoft, aunque la revista alemana Der Spiegel menciona como su propietario a Jeff Bezos, fundador y director ejecutivo de Amazon.
Pero, ¿cómo llegó el Palimpesto de Arquímedes hasta la casa de subastas Christie’s? Después de la guerra greco-turca (1919-1922) derivada de la primera guerra mundial, la biblioteca del Patriarcado de Jerusalén en Constantinopla fue cerrada y los 827 manuscritos que se conservaban, de los 890 catalogados por Papadopoulos-Kerameus, fueron enviados a la Biblioteca Nacional de Grecia, en Atenas, aunque no todos llegarían, como fue el caso de este palimpsesto.
En 1923 el manuscrito fue comprado por Marie Louis Sirieix, un hombre de negocios de París que estaba de viaje por Oriente, supuestamente a un monje, pero no existió ningún documento que registrase la compra-venta del mismo.
Por desgracia, el palimpesto fue deteriorándose desde entonces. Sirieix escondió el manuscrito en su casa de París, probablemente en el sótano, donde sufrió daños causados por el agua, el humo y el moho. Además, se realizaron en cuatro folios del mismo cuatro dibujos a color de los Apóstoles, imitando el estilo bizantino, falsificaciones que pretendían incrementar el valor del manuscrito. Sin ser conscientes del valor que realmente tenía.
Una década antes de morir, en 1956, Sirieix dejó el manuscrito a su hija, quien a partir de 1970 empezó a investigar sobre el posible valor del mismo. Y así es como acabaría llegando a la casa de subastas Chistie’s en la década de 1990.
Volviendo a la subasta del Palimpsesto de Arquímedes, su nuevo propietario lo prestó al Museo Walters de Arte de Baltimore, en Maryland, EE.UU., para su conservación, para la realización de un potente estudio, con técnicas muy avanzadas como técnicas de imagen multi-espectal o florescencia de rayos X, para desvelar el contenido oculto en el mismo, y para la exhibición de las mismas.


Se puede leer más sobre el complicado proceso de recuperación de las imágenes del Palimpsesto de Arquímedes en la página web The Archimedes Palimpsest Project, del Museo Walters de Arte de Baltimore.

Sobre toda esta truculenta historia se ha escrito un libro, con el título (en castellano) de El código de Arquímedes, de Reviel Netz y William Noel, publicado por Temas de Hoy, en 2007.
Pero, como decía al inicio de esta entrada, mi intención era escribir sobre el puzzle geométrico, de tipo Tangram, llamado Stomachion. Este puzzle fue descrito por el matemático griego Arquímedes en la obra homónima, el Stomachion, quees una de las siete incluidas en el Palimpsesto de Arquímedes. De hecho, es la copia más extensa que existe de la misma, aunque solo se incluye un fragmento, de una única página, que además es la parte introductoria de la misma.


Como decíamos el Stomachion es un puzle geométrico de tipo Tangram, formado por una descomposición del cuadrado en 14 piezas poligonales, que incluyen 11 triángulos, 2 cuadriláteros y 1 pentágono, como puede verse en una de las imágenes anteriores. Recordemos que el conocido Tangram (véase la entrada Tangram) es una descomposición del cuadrado en 7 piezas poligonales, 5 triángulos, 1 cuadrado y 1 paralelogramo de tipo romboide, cuya imagen también hemos incluido.
Además del texto Stomachion de Arquímedes, existen muchas referencias a este rompecabezas geométrico de autores latinos, como el poeta y filósofo romano Titus Lucretius Carus (99 – 55 a.n.e.), el poeta romano Gaius Caesius Bassus (siglo I), el poeta y retórico romano Decimus Magnus Ausonius (aprox. 310 – 390), el filólogo, retórico y filósofo romano Gaius Marius Victorinus (siglo IV), quien dicen que murió en la erupción del Vesubio o el poeta y retórico galo-romano Magnus Félix Ennodius (473/4 – 521), obispo de Pavía. Algunos autores, como Ausonius, se refieren también al puzle como Ostomachion, palabra de origen griego formada por ὀστέον (osteon, “hueso”), seguramente en referencia a que las piezas estaban fabricadas con hueso, y μάχη (machē, “lucha”), y también se conoce como “Loculus (caja) de Arquímedes”, quizás porque las piezas se colocaban, para resolver el puzle, en una caja cuadrada.
La construcción de la caja de Arquímedes es la siguiente (véase la imagen de abajo). Consideremos un cuadrado ABCD, llamemos E, F, G, H a los puntos medios de los lados AB, BC, CD y DA; dibujemos los segmentos HB, HF y HC y sean J, K, L los puntos medios de estos segmentos; dibujamos el segmento AKC, que corta a HB en el punto que denominaremos M; ahora sea N el punto medio se AM y P el punto medio de BF; dibujemos BN; dibujemos AP, que corta al segmento HB en un punto, que llamamos Q, y borramos el segmento AQ; dibujemos PJ; dibujemos un segmento que empiece en B y pase por J hasta encontrar al segmento CD en un punto que llamaremos R, para después borrar la parte del segmento BL; dibujemos el segmento FL, que cortara a AC en un nuevo punto, S; y finalmente, dibujemos el segmento LG. Las líneas dibujadas sobre el cuadrado original ABCD, lo dividen en las 14 piezas del puzle.
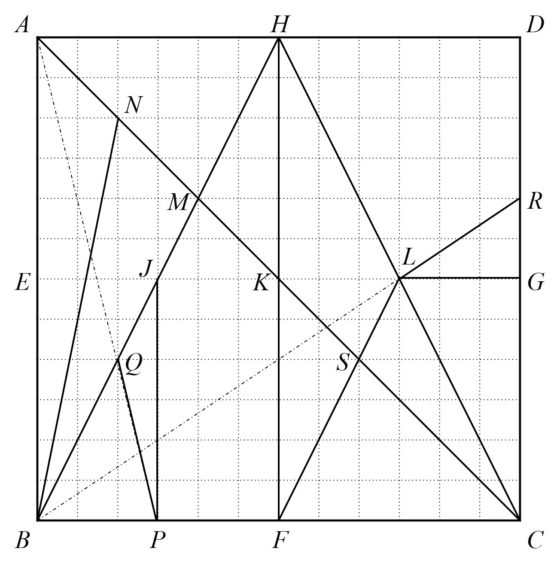
Si observamos la cuadrícula, de tamaño 12 x 12, que hemos dibujado en la imagen anterior, resulta que todos los puntos de la construcción del puzle, que son los vértices de las piezas, están sobre los puntos de intersección de la cuadrícula.
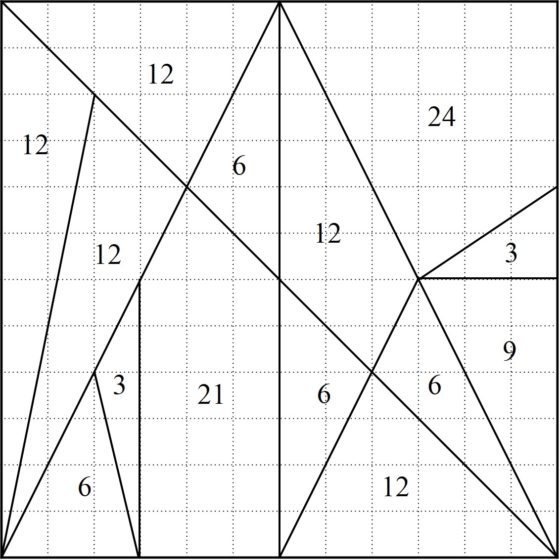
Más aún, si tomamos el área del cuadradito de la cuadrícula como área 1 (es decir, el cuadrado pequeño tiene lado 1 y el grande 12), podemos calcular fácilmente las superficies de todas las piezas (lo cual es un problema sencillo de cálculo de áreas, que incluso se puede realizar en el aula, en clase de matemáticas) y descubriremos que todas tienen área entera, en concreto, las siguientes áreas (desde arriba a la izquierda, siguiendo el orden de las agujas del reloj, más o menos): 12, 6, 12, 24, 3, 9, 6, 12, 6, 21, 3, 6, 12 y 12.
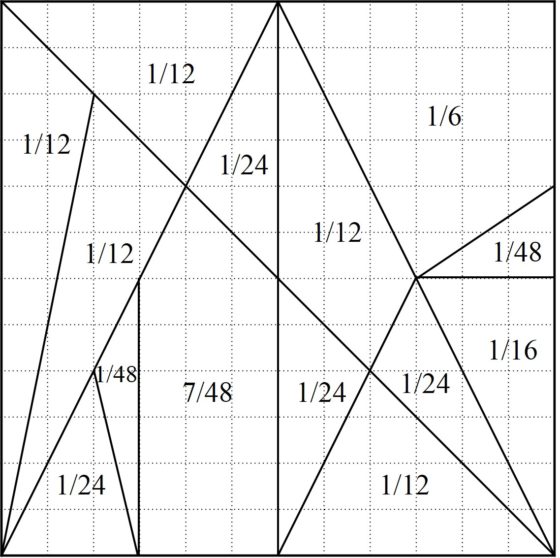
O lo que es lo mismo, cada una de las piezas del rompecabezas tiene la siguiente fracción del total (siguiendo el mismo orden que arriba): 1/12, 1/24, 1/12, 1/6, 1/48, 1/16, 1/24, 1/12, 1/24, 7/48, 1/48, 1/24, 1/12 y 1/12, ya que la superficie total del cuadrado grande es 144 (según las medidas anteriores).
Por lo tanto, ya sabemos cómo construir este rompecabezas geométrico, de tipo Tangran, conocido como Stomachion, Ostomachion o caja de Arquímenes, y ya estamos en condiciones de poder jugar con el mismo intentando construir el cuadrado o formando diferentes figuras (el elefante de la siguiente imagen, un triángulo y muchas otras), como se hace con el conocido Tangram.

Pero volviendo al fragmento de la obra Stomachion que aparece en el Palimpsesto de Arquímedes, este despistó completamente a los expertos, ya que aparentemente describía un juego infantil sin ningún interés científico. Y no parece ser que este sea un tema a la altura del gran sabio griego. La siguiente entrada de esta mini-serie de la sección Matemoción del Cuaderno de Cultura Científica la dedicaremos a analizar un poco más este antiguo puzle griego y a tratar de averiguar si solo se trataba de un sencillo juego infantil.
Bibliografía
2.- Wikipedia: Palimpsesto
3.- The Archimedes Palimpsest Project en el The Walters Art Museum (Baltimore, Maryland)
4.- Frank J. Swetz, Mathematical Treasure: The Archimedes Palimpsest, Convergence, MAA, 2013
5.- The Archimedes Palimpsest, Sale 9058, Christie’s
6.- Mathias Schulz, The Story of the Archimedes Manuscript, Spiegel, 2007
7.- Reviel Netz, William Noel, El código de Arquímedes, Temas de Hoy, 2007
8.- Reviel Netz, Fabio Acerbi, Nigel Wilson, Towards a Reconstruction of Archimedes’ Stomachion, SCIAMV 5, pp. 67-99, 2004.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Minoldo Gramajo González
¡Un delicioso bocadillo científico para ser degustado lentamente! Gracias por compartirlo.
Contribuye mucho a valorar la obra de los grandes de la antigüedad.
RAUL IBAÑEZ TORRES
Muchísimas gracias Minoldo,
Un fuerte abrazo, R
Angel Ferrández
Precioso artículo, Raúl. Puedo imaginar el trabajo que hay tras él y lo valoro todavía más. Enhorabuena.
Enlaces Recomendados de la Semana (N°537)
[…] El puzzle Stomachion y el palimpsesto de Arquímedes: “En esta mini-serie de dos entradas del Cuaderno de Cultura Científica me gustaría hablar del puzzle geométrico de tipo Tangram más antiguo que se conoce, el Stomachion. Pero antes de hablar de este puzzle geométrico, me parece interesante que empecemos esta historia por el palimpsesto de Arquímedes, que incluye la copia más extensa de la obra original Stomachion del matemático griego.” […]
El puzzle Stomachion y el palimpsesto de Arquímedes (2) — Cuaderno de Cultura Científica
[…] primera entrada de esta mini-serie de la sección Matemoción del Cuaderno de Cultura Científica, El puzzle Stomachion y el palimpsesto de Arquímedes (1), habíamos descrito el rompecabezas conocido como Stomachion, o caja de Arquímedes, e incluso […]
El Palimpsesto de Arquímedes | gAZeta
[…] tomada de Cultura Científica, editada por Vinicio Barrientos […]