Un buen chiste matemático es mejor, y mejor matemática, que una docena de publicaciones mediocres.

John Edensor Littlewood, A Mathematician’s Miscellany, 1953

El matemático británico John Edensor Littlewood (1885-1977) publicó en 1953 su autobiografía, A Mathematician’s Miscellany, que contenía numerosas anécdotas. Se reeditó en 1986, añadiendo más contenidos, bajo el título de Littlewood’s miscellany.

En este último libro, Littlewood utiliza ese sentido del humor al que alude la cita inicial para enunciar la llamada ley de Littlewood que establece que «una persona puede esperar que le suceda un milagro aproximadamente una vez al mes». Pero, ¿qué es un milagro? Littlewood lo define así:

Un evento extraordinario que tiene un significado especial y ocurre con una frecuencia de uno entre un millón.

Y el matemático argumenta entonces de la siguiente manera:

Mientras una persona está despierta puede percibir ‘un evento’ por segundo, evento que puede ser ordinario o extraordinario. Supongamos que una persona es ‘receptiva’ aproximadamente durante ocho horas al día. Así, experimenta 28.800 eventos al día –una hora tiene sesenta minutos y cada minuto sesenta segundos: son 8x60x60–. Así, en 35 días, una persona experimentará 1.008.000 de eventos. Según la definición dada de milagro, una persona puede esperar un acontecimiento milagroso cada 35 días.

Es decir, según Littlewood, los milagros no son tan extraños, ni tienen que ver con poderes sobrenaturales. En efecto, tan solo hay que tener en cuenta la ley de los grandes números…

En A Mathematician’s Miscellany, Littlewood describe un problema conocido actualmente como la paradoja de Ross-Littlewood. Toma su nombre del matemático Sheldon Ross (1943) quien lo detalló en su libro A First Course of Probability (1988). Esta paradoja intenta ilustrar los problemas conceptuales relacionados con la noción de supertarea –sucesión infinita numerable de operaciones que se producen secuencialmente en un intervalo de tiempo finito–.

Planteamiento del problema

Tenemos un jarrón vacío y una cantidad infinita numerable de bolas a nuestra disposición. En cada paso –recordemos que hay un número infinito de ellos– se agregan 10 bolas al jarrón y se retira 1 bola del mismo. Se supone que el jarrón está vacío un minuto antes del mediodía, y que se realizan los infinitos pasos de la manera siguiente:

• el primer paso se realiza 30 segundos antes del mediodía;

• el segundo paso se realiza 15 segundos antes del mediodía;

• así, cada paso siguiente se realiza en la mitad del tiempo del paso anterior, es decir, el paso n se realiza 2⁻ⁿ minutos antes del mediodía.

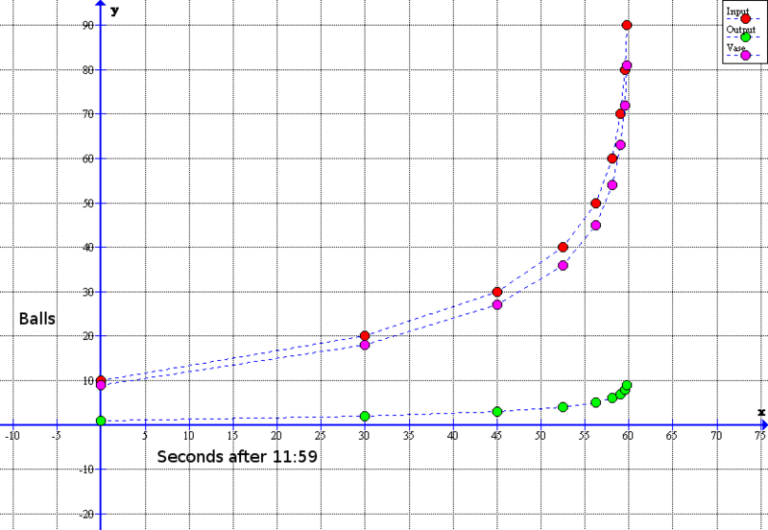
Continuando de este modo, transcurrido un minuto, se han realizado una cantidad infinita numerable de pasos. La pregunta es: «¿cuántas bolas hay en el jarrón al mediodía?».

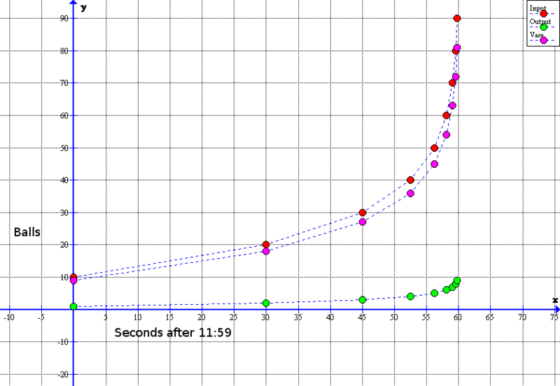
No hay una única respuesta como veremos a continuación, y de allí que hablemos de paradoja… ¿Quizás estemos asistiendo a ese acontecimiento milagroso que es posible que nos ocurra este mes de noviembre?

Algunas respuestas a la pregunta

1. El jarrón contiene infinitas bolas

En efecto, en cada paso se añaden más bolas de las que se eliminan. Es decir, en cada paso habrá un número mayor de bolas que en el paso anterior. Así, si el número de bolas aumenta en cada paso y hay un número infinito de ellos, habrá infinitas de bolas al mediodía.

2. El jarrón está vacío

Supongamos que las bolas están numeradas. Argumentamos del siguiente modo: en el paso 1 se meten en el jarrón las bolas 1 a 10 y se saca la bola número 1. En el paso 2, se introducen las bolas numeradas 11 a 20, y se retira la bola 2. Si se continúa de este modo, al mediodía, la bola número n introducida en el jarrón se elimina en un paso posterior –en el paso n–. Así, si cualquier bola se extrae en alguno de los pasos, el jarrón está obviamente vacío al mediodía.

3. Depende de las condiciones

Esta respuesta afirma que la cantidad de bolas contenidas en el jarrón al mediodía depende del orden en el que se sacan las bolas del jarrón. Antes hemos visto la manera en la que se consigue demostrar que el jarrón está vacío al mediodía. Supongamos ahora que la bola número 10 se retira del jarrón en el paso 1, la bola número 20 en el paso 2, y así sucesivamente. Procediendo de esta manera, es claro que al mediodía quedan infinitas bolas en el jarrón.

Pero, más aún, es posible razonar de manera que, al mediodía, queden cualquier número de bolas –n– en el jarrón. En efecto, si p es el número de paso que se está realizando, se procede del siguiente modo:

• se ponen las bolas numeradas 10p-9 a 10p en el jarrón,

• si p≤n, se saca la bola número 2p,

• si p>n, se saca la bola número n+p del jarrón.

Procediendo de este modo, es claro que las n primeras bolas impares no se sacan del jarrón, mientras que todas las bolas mayores o iguales a 2n sí se eliminan. Así, a mediodía quedan exactamente n bolas en el jarrón.

4. El problema no está bien especificado

Lo que sucede con las bolas y el jarrón está determinado en cada momento antes del mediodía, pero no es posible concluir lo que sucede después del mediodía.

5. El problema está mal planteado

Si deben realizarse infinitos pasos de manera secuencial antes del mediodía, el mediodía es un punto en el tiempo que no se puede alcanzar. Además, preguntar cuántas bolas quedarán en el jarrón al mediodía es asumir que se llegará a ese momento del día. Por lo tanto, hay una contradicción implícita en el planteamiento del problema.

¿Cuál de estas respuestas te convence más?

Referencias

• John Edensor Littlewood, A Mathematician’s Miscellany, Methuen and Co, 1953

• Béla Bollobás (ed.),Littlewood’s miscellany, Cambridge University Press, 1986

• Paradoja de Ross-Littlewood, Wikipedia (consultado el 23 de noviembre de 2019)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.